2025春训第八场
 Star
StarTable of contents
这次训练赛主打一个特殊情况 RE,不细心一点有一万个坑能让程序炸掉……
A. 能量传输
不难(不容易)发现,k 越小聚集到的位置越多,操作次数越小,所以做法是
统计 1 的个数,找到除了 1 以外的最小的约数作为 k;
每 k 个 1 分成一组,各组独立计算最小操作次数;
使得操作数最小的位置一定是中位数,所以把到位置中位数的距离求和即可。
注意特判 0 个,会炸掉!!!
#include <iostream>
#include <cmath>
#include <vector>
#define int long long
using namespace std;
int a[100010], b[100010];
int len;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n, s = 0, l;
cin >> n;
for (int i = 1; i <= n; ++i) {
cin >> a[i];
s += a[i];
}
if (s == 0) {
cout << 0 << endl;
return 0;
}
l = sqrt(s);
int t = s;
for (int i = 2; i <= l; ++i) {
if (s % i == 0) {
t = i;
break;
}
}
long long res = 0;
for (int i = 1; i <= n; ++i) {
if (a[i]) b[++len] = i;
if (len == t) {
int pos = b[(len + 1) / 2];
for (int j = 1; j <= len; ++j) {
res += abs(b[j] - pos);
}
len = 0;
}
}
cout << res << endl;
return 0;
}
B. 能源危机
你说的对,但是我可以用 Python,用 C++ 写高精的话大概思路就是除数后面补零直到最高位和被除数对齐,减到不能再减,然后除数删一个零继续减,高精全家桶传送门。
import sys
sys.set_int_max_str_digits(300000)
a = int(input())
b = int(input())
print(a // b)
C. 鲁星救援
没什么技术含量,来来回回搜的很恶心。先从 s 搜到 p,把路上的点全都标记上;然后,把标记上的点都加到一个新队列里,搜 t 即可。
- ps:注意按照题目说的顺序搜。
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
/*
上代表 1,右代表 2,下代表 3,左代表 4
*/
const int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
int a[1010][1010];
int dis[1010][1010];
bool vis[1010][1010];
pair<int, int> pre[1010][1010];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n, m, sx, sy, tx, ty, px, py;
cin >> n >> m >> sx >> sy >> tx >> ty >> px >> py;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
cin >> a[i][j];
}
}
// 边界全都堵上,防止搜出去数组越界 RE
for (int i = 1; i <= n; ++i) a[i][0] = a[i][m + 1] = 1;
for (int i = 1; i <= m; ++i) a[0][i] = a[n + 1][i] = 1;
queue<pair<int, int>> q;
q.push({sx, sy});
vis[sx][sy] = true;
bool f = false;
while (!q.empty()) {
auto x = q.front();
q.pop();
if (x == make_pair(px, py)) {
f = true;
while (!q.empty()) {
q.pop();
}
memset(vis, 0, sizeof(vis));
if (pre[x.first][x.second] == make_pair(0, 0)) {
vis[sx][sy] = true;
dis[sx][sy] = 1;
q.push({sx, sy});
break;
}
do {
q.push(x);
dis[x.first][x.second] = 1;
vis[x.first][x.second] = true;
x = pre[x.first][x.second];
} while (x != make_pair(sx, sy));
vis[sx][sy] = true;
dis[sx][sy] = 1;
q.push(make_pair(sx, sy));
break;
}
for (int i = 0; i < 4; ++i) {
auto y = x;
y.first += dx[i], y.second += dy[i];
if (a[y.first][y.second] || vis[y.first][y.second]) continue;
pre[y.first][y.second] = x;
vis[y.first][y.second] = true;
q.push(y);
}
}
if (!f) {
cout << -1 << endl;
return 0;
}
while (!q.empty()) {
auto x = q.front();
q.pop();
for (int i = 0; i < 4; ++i) {
auto y = x;
y.first += dx[i], y.second += dy[i];
if (dis[y.first][y.second] || a[y.first][y.second]) continue;
dis[y.first][y.second] = dis[x.first][x.second] + 1;
q.push(y);
}
}
cout << dis[tx][ty] - 1 << endl;
return 0;
}
E. 俄罗斯方块 (tetris)
简化版:覆盖墙壁.
我做这道题的时候用线性的 dp 打表找规律做的,实际上是可以直接推出来的。
最后三个方块只要放进去一定会堵死,直接忽略;枚举最后一个完整的矩形块的形状,只有以下四种形状
两个 1 × 4 的方块并排;
一个 2 × 2 的方块;
两个相同 L 形方块,中间可以夹多个 1 × 4 的方块;
两个不同 L 形方块 + 一个 1 × 4 的方块,中间同样可以夹多个 1 × 4 的方块。
如下图
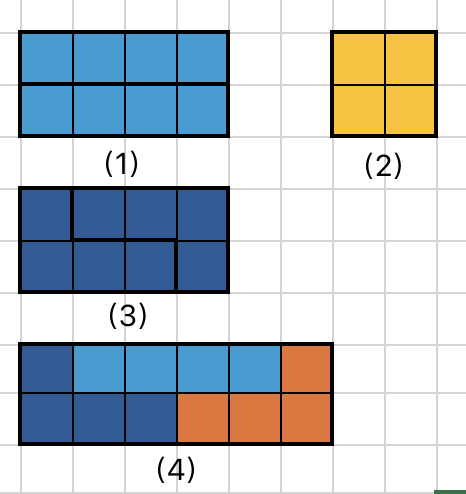
计 \(f_i\) 为 2 × i 时的方案数,不难得出
\[f_i = f_{i - 4} + f_{i - 2} + 2 (f_{i - 4} + f_{i - 8} + \dots) + 2 (f_{i - 6} + f_{i - 10} + \dots)\]
维护一个 f 数组的前缀和即可得到线性的做法。
#include <iostream>
#include <cmath>
using namespace std;
const int MOD = 1000000007;
int f[10000010];
int s[10000010], s2[10000010];
int main() {
int n;
while (cin >> n) {
f[0] = 1;
s[0] = 1;
for (int i = 1; i <= n; ++i) {
f[i] = 0;
if (i - 2 >= 0) f[i] = (f[i] + f[i - 2]) % MOD;
if (i - 4 >= 0) f[i] = (f[i] + f[i - 4]) % MOD;
if (i >= 4) f[i] = (f[i] + 2 * s[i - 4] % MOD) % MOD;
if (i >= 6) f[i] = (f[i] + 2 * s[i - 6] % MOD) % MOD;
if (i >= 4) s[i] = (f[i] + s[i - 4]) % MOD;
else s[i] = f[i];
}
cout << f[n] << endl;
}
return 0;
}
显然这还不够,数据范围是 1e18 还需要再优化,于是又到了喜闻乐见的矩阵快速幂环节。
显然奇数是不可能的,对于偶数的情况重新编号一下(好看)
\[f_i = f_{i - 1} + f_{i - 2} + 2 (f_{i - 2} + f_{i - 4} + \dots) + 2 (f_{i - 3} + f_{i - 5} + \dots)\]
后面两项可以合并
\[f_i = f_{i - 1} + f_{i - 2} + 2 \sum_{j = 0}^{i - 2}{f_j}\]
这样就好构造矩阵了,其中 \(s_i = \sum_{j = 0}^i{f_j}\)
\[\begin{pmatrix} f_{i - 2} & f_{i - 1} & s_{i - 2} \end{pmatrix} \begin{pmatrix} 0 & 1 & 0\\ 1 & 1 & 1\\ 0 & 2 & 1\\ \end{pmatrix} = \begin{pmatrix} f_{i - 1} & f_{i} & s_{i - 1} \end{pmatrix}\]
累乘可以得到
\[\begin{pmatrix} 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} 0 & 1 & 0\\ 1 & 1 & 1\\ 0 & 2 & 1\\ \end{pmatrix} ^{n - 1} = \begin{pmatrix} f_{n - 1} & f_{n} & s_{n - 1} \end{pmatrix}\]
#include <iostream>
#include <vector>
using namespace std;
const int MOD = 1000000007;
vector<vector<int>> mul(vector<vector<int>> a, vector<vector<int>> b) {
vector<vector<int>> res(3, vector<int>(3, 0));
for (int k = 0; k < 3; ++k) {
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
res[i][j] = (res[i][j] + (long long)a[i][k] * b[k][j] % MOD) % MOD;
}
}
}
return res;
}
int main() {
long long n;
while (cin >> n) {
if (n & 1) cout << 0 << endl;
else {
n >>= 1;
n--;
vector<vector<int>> mat = {
{0, 1, 0},
{1, 1, 1},
{0, 2, 1}
},
res = {
{1, 0, 0},
{0, 1, 0},
{0, 0, 1}
};
while (n) {
if (n & 1) res = mul(res, mat);
mat = mul(mat, mat);
n >>= 1;
}
cout << ((long long)res[1][0] + res[1][1] + 2 * res[1][2]) % MOD << endl;
}
}
return 0;
}
Subscribe to my newsletter
Read articles from Star directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Star
Star
A Chinese OIer and a tosser.