P vs NP: Computational Complexity and Solutions in Operations Research

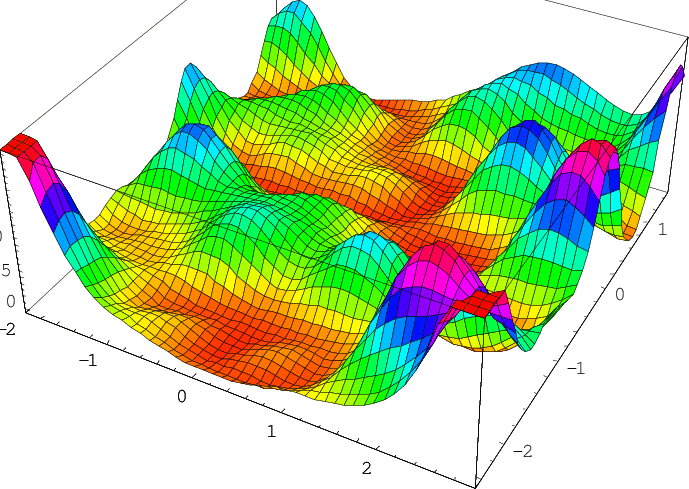
1. Introduction

Computational complexity theory is one of the cornerstones of computer science, dedicated to classifying problems based on their intrinsic level of difficulty. Within this field, P and NP problems occupy a central role, challenging researchers and professionals to understand the limits of what can or cannot be computed efficiently.

The distinction between these two classes not only shapes the development of algorithms and computing systems but also has profound implications in areas such as cryptography, optimization, and operations research.

This article explores the fundamental concepts of P and NP problems, their impact on the computing landscape, and their role in operations research, highlighting the relevance of these challenges to modern science and technology.

2. What are P and NP Problems?

2.1 P Problems: Tractable and Efficiently Solvable

P problems are a class of decision problems that can be solved by a deterministic Turing machine in polynomial time. This means that the time required to solve the problem grows as a polynomial function of the input size, making them computationally "tractable" or efficient to solve.

2.2 NP Problems: Verifiable but Not Necessarily Solvable Efficiently

NP problems are a class of decision problems for which a proposed solution can be verified by a deterministic Turing machine in polynomial time. However, finding such a solution may require exponential time in the worst case. NP stands for "nondeterministic polynomial time", referring to the ability of a nondeterministic Turing machine to solve these problems in polynomial time by "guessing" the correct solution.

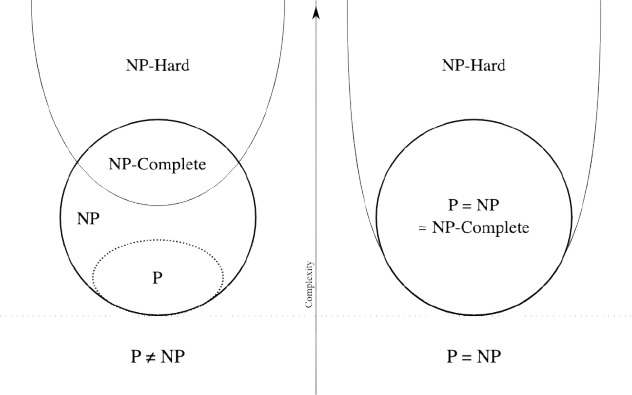
2.3 NP Complete Problems: The Hardest Problems in NP

NP-complete problems are a subset of NP problems that have two key properties:

1. They are in NP (solutions can be verified in polynomial time).

2. They are NP-hard, meaning that every problem in NP can be reduced to them in polynomial time.

2.4 NP Hard Problems

NP-hard problems are a class of problems that are at least as hard as the hardest problems in NP. This means that if you can solve any NP-hard problem in polynomial time, then every problem in NP can also be solved in polynomial time. In other words, a polynomial-time solution to an NP-hard problem would imply that P = NP, one of the most profound unsolved questions in computer science.

However, unlike NP-complete problems, NP-hard problems do not necessarily belong to the class NP. They can be even harder than NP problems, and some may not even be decision problems (e.g., optimization problems). In fact, certain NP-hard problems may be undecidable, meaning there is no algorithm that can solve them for all possible inputs.

Reference: https://www.sciencedirect.com/science/article/pii/S1568494613001944

3. The Influence on Operations Research

Operations Research (OR) is a field dedicated to optimizing complex decision-making processes, and it heavily relies on solving problems that often fall into the NP-hard category. These problems are very present in real-world applications, ranging from logistics and supply chain management to scheduling and resource allocation. Despite their computational complexity, advances in modeling and algorithm design have enabled researchers and practitioners to tackle these challenges effectively.

3.1 How Do We Solve NP-hard Problems if They Are So Hard?

Given that NP-hard problems are computationally intractable for large instances—meaning that finding an optimal solution in a reasonable amount of time is often impossible—we must turn to alternative approaches. This leads to an important question: Can we accept solutions that are less than optimal? In other words, can we settle for a good solution that may not be the best possible but is still practical and useful?

The answer is yes, and this is where heuristics and their more advanced counterparts, metaheuristics, come into play.

3.2 What Are Heuristics and Why Are They Useful?

Heuristics are problem-solving techniques that aim to find good-enough solutions in a reasonable amount of time, even if they do not guarantee optimality. They are particularly valuable for NP-hard problems because they provide a way to navigate the enormous solution space efficiently, avoiding the exponential time complexity of exact methods.

Key Characteristics of Heuristics:

1. Speed: Heuristics are designed to produce solutions quickly, making them suitable for real-world applications where time is critical.

2. Approximation: They often trade off optimality for practicality, delivering solutions that are "good enough" for the problem at hand.

3. Flexibility: Heuristics can be tailored to specific problem domains, allowing them to exploit problem-specific structures or patterns.

3.4 Types of Heuristics and Metaheuristics

1. Simple Heuristics:
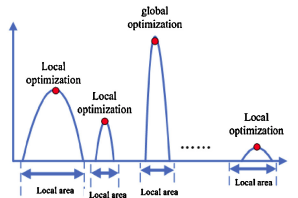
   These are rule-of-thumb methods that provide quick solutions. Examples include:

   • Greedy Algorithms: Make locally optimal choices at each step, hoping to find a global optimum (e.g., the nearest neighbor heuristic for the Traveling Salesman Problem).

   • Constructive Heuristics: Build a solution incrementally, adding one element at a time (e.g., scheduling tasks based on earliest due dates).

2. Metaheuristics:
   These are more sophisticated frameworks that guide the search for solutions in a structured yet flexible way. Examples include:

   • Simulated Annealing: Mimics the annealing process in metallurgy, allowing occasional "worse" moves to escape local optima.

   • Genetic Algorithms: Inspired by natural selection, they evolve a population of solutions over generations.

   • Tabu Search: Uses memory structures to avoid revisiting recently explored solutions, promoting diversification.

   • Ant Colony Optimization: Models the behavior of ants foraging for food, using pheromone trails to guide the search.

   • Variable Neighborhood Descent (VND): Is a local search technique that uses multiple neighborhoods to refine a solution. It explores each neighborhood sequentially, improving the solution until no further enhancements are possible. It is efficient but can get stuck in local optimals.

   • Variable Neighborhood Search (VNS) : Combines VND with a perturbation phase ("shaking") to escape local optimals. It alternates between perturbing the solution and refining it with VND, exploring the solution space more broadly. VNS is more robust and suitable for complex problems.

     

     Reference: https://www.sciencedirect.com/science/article/pii/S1568494613001944

Reference: https://www.researchgate.net/figure/D-plots-of-the-special-group-of-global-optimization-functions-Credit-37-38-39_fig2_330511377

3.5 Why Accept Suboptimal Solutions?

In practice, the pursuit of optimality is often impractical or unnecessary for several reasons:

1. Time Constraints: Many real-world problems require decisions to be made quickly, leaving no time for exhaustive search methods.

2. Complexity of Real-World Problems: Real-world scenarios often involve uncertainties, dynamic changes, and incomplete information, making optimal solutions less meaningful.

By accepting suboptimal but high-quality solutions, we can achieve significant improvements in efficiency, cost savings, and decision-making without the computational complexity of finding the absolute best solution.

3.6 Alternatives To Find Optimal Solutions

For problems where near-optimal solutions are insufficient, mathematical optimization techniques like linear programming (LP) and integer linear programming (ILP) provide powerful frameworks to find exact solutions. These methods rely on mathematical models to represent problems in terms of linear equations and inequalities, which can then be solved using algorithms like the Simplex method or interior-point methods.

To handle large-scale or complex problems, commercial solvers such as CPLEX, Gurobi, and Google OR-Tools are widely used. These solvers incorporate advanced algorithms, parallel processing, and heuristics to efficiently find optimal or near-optimal solutions. While they are highly effective, their performance depends on the problem's structure and size, and they may still struggle with NP-hard problems as instances grow.

In this article, we talk mainly about heuristics. In other occasion, i intend to write more about methods that leads to optimal solutions.

4. Conclusion

The study of P and NP problems is central to understanding computational limits.

While P problems are efficiently solvable, NP-hard problems pose significant challenges due to their complexity. In operations research, where many real-world problems are NP-hard, heuristics and metaheuristics provide practical ways to find high-quality solutions quickly, even if they are not optimal.

Although this article focuses on heuristics, mathematical optimization techniques and commercial solvers offer alternative approaches for finding optimal solutions, which will be explored in future discussions.

Thank you for reading this article. I hope I was able to share with you some insights into computing theory and optimization techniques.