Understanding the Basics of Recursion

Understanding the Image

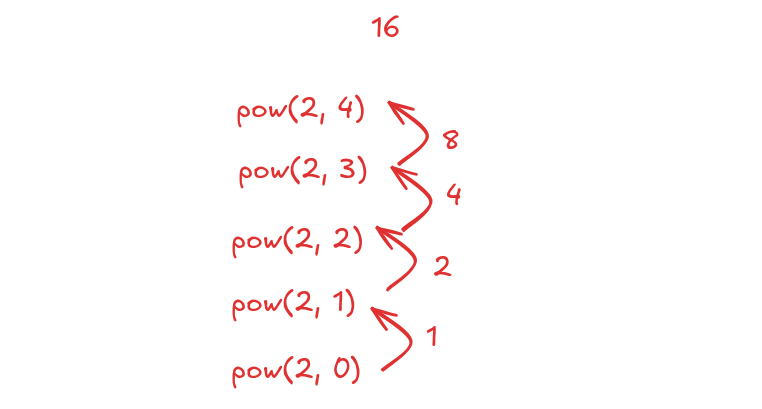
The image demonstrates how the power function (specifically, calculating powers of 2) can be implemented recursively. It shows the following steps:

1. Base Case: pow(2, 0) = 1 (Any number raised to the power of 0 is 1).

2. Recursive Step: pow(2, n) = pow(2, n-1) * 2 for n > 0.

The image walks through the calculation of pow(2, 4):

• pow(2, 4) = pow(2, 3) * 2

• pow(2, 3) = pow(2, 2) * 2

• pow(2, 2) = pow(2, 1) * 2

• pow(2, 1) = pow(2, 0) * 2

• pow(2, 0) = 1

Then, it substitutes the results back up the chain:

• pow(2, 1) = 1 * 2 = 2

• pow(2, 2) = 2 * 2 = 4

• pow(2, 3) = 4 * 2 = 8

• pow(2, 4) = 8 * 2 = 16

Recursive Java Code:

Java

public class PowerOfTwo {
    public static int pow(int n) {
        if (n == 0) {
            return 1; // Base case: 2^0 = 1
        } else {
            return pow(n - 1) * 2; // Recursive step: 2^n = 2^(n-1) * 2
        }
    }
    public static void main(String[] args) {
        int exponent = 4;
        int result = pow(exponent);
        System.out.println("pow(2, " + exponent + ") = " + result); 
        // Output: pow(2, 4) = 16
    }
}

Explanation

1. pow(int n) Method:

   • Takes an integer n as input, representing the exponent.

   • Base Case: If n is 0, it returns 1 (since 2 raised to the power of 0 is 1).

   • Recursive Step: If n is not 0, it calls itself with n - 1 and multiplies the result by 2. This implements the pow(2, n) = pow(2, n-1) * 2 logic.

2. main Method:

   • Sets the exponent to 4 (as in the image).

   • Calls the pow method to calculate 2 raised to the power of 4.

   • Prints the result.

How the Recursion Works

1. When pow(4) is called, it doesn't immediately know the answer. It calls pow(3) and waits for the result.

2. pow(3) calls pow(2), pow(2) calls pow(1), and pow(1) calls pow(0).

3. pow(0) hits the base case and returns 1.

4. The value 1 is passed back to pow(1), which calculates 1 * 2 = 2 and returns 2.

5. This 2 is passed back to pow(2), which calculates 2 * 2 = 4 and returns 4.

6. The process continues until pow(4) receives 8 from pow(3), calculates 8 * 2 = 16, and returns 16.

Key Points

• Base Case: A recursive function must have a base case to stop the recursion. Without it, the function would call itself infinitely.

• Recursive Step: The recursive step breaks the problem down into smaller subproblems and calls the function itself to solve those subproblems.

• Stack Frames: Each recursive call creates a new stack frame, which stores the function's local variables and parameters. This is how the function "remembers" its state between calls.