Day 7: Multiple Linear Regression – Predicting with Multiple Factors
 Saket Khopkar
Saket Khopkar
In the previous blog, we learned how Simple Linear Regression helps predict a continuous value (like house prices) based on one factor (like house size). But in real-world, things are more complex.
For example, a car’s price depends on:
✅ Horsepower (More power = More expensive)
✅ Mileage (More mileage = Less expensive)
✅ Brand (Luxury brands cost more)
✅ Year of Manufacture (Newer cars cost more)
This is where Multiple Linear Regression (MLR) comes in. Instead of just one independent variable, MLR allows us to use multiple factors to make better predictions.
Getting to know today’s topic
Multiple Linear Regression (MLR) is an extension of Simple Linear Regression that uses two or more independent variables to predict a dependent variable.
Think of it this way:
Simple (Linear) Regression: "How much does house size affect the price?"
Multiple Regression: "How do house size, number of bedrooms, and location affect the price?"
Just like that; things in real-world needs to be introspected from multiple angles before making a decision.
You may get to know more about this concept by looking at the example below:
Imagine you run a used car dealership. Customers want to know how much their car is worth.
A car’s price doesn’t depend on just one thing—it depends on multiple factors like:
Horsepower: More horsepower = More expensive.
Mileage: More mileage = Less expensive.
Year: Older cars are cheaper.
Brand: Luxury brands like BMW cost more. (Because it matters bro!!)
For our example, have a look at below table:
| Horsepower | Mileage (1000s) | Year | Brand (Luxury = 1 ; Ecconomy = 0) | Price ($) |
| 150 | 50 | 2018 | 1 | 25,000 |
| 120 | 80 | 2016 | 0 | 15,000 |
| 200 | 30 | 2020 | 1 | 40,000 |
| 130 | 70 | 2017 | 0 | 18,000 |
We will train a model to predict car prices based on these features.
Equation
In Simple Regression, we had one independent variable:
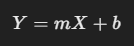
But the case isn’t same for Multiple Linear Regression, as it tends to have multiple variables. So the formula for the same stands:
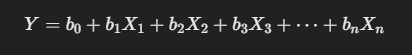
Y = Dependent variable (e.g., Price of the car)
X₁, X₂, X₃, ... Xₙ = Independent variables (e.g., Mileage, Horsepower, Year)
b₀ = Intercept (base price of a car with all values at 0)
b₁, b₂, b₃, ... bₙ = Slopes (how much each variable affects the price)
Usually I tend not go mathematical while writing so I will be providing an example that you understand.
Price = 5000 + (150 × Horsepower) − (200 × Mileage) + (1000 × Year) + (5000 × Luxury)
Then, for a BMW (Luxury=1) with 150 HP, 50k mileage, and from 2018, it should be as below:
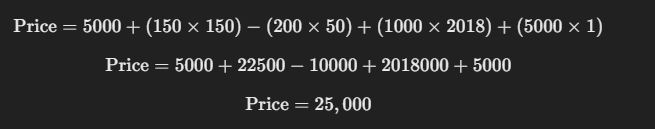
As you can see, it matches the value perfectly as in above table.
Alright, time for coding. Get your Jupyter Notebooks ready.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
# Creating the dataset
data = {
"Horsepower": [150, 120, 200, 130, 180],
"Mileage": [50, 80, 30, 70, 40],
"Year": [2018, 2016, 2020, 2017, 2019],
"Luxury": [1, 0, 1, 0, 1],
"Price": [25000, 15000, 40000, 18000, 35000]
}
df = pd.DataFrame(data)
# Defining features (X) and target (Y)
X = df[["Horsepower", "Mileage", "Year", "Luxury"]]
y = df["Price"]
# Splitting into 80% training and 20% testing
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Predict car prices
predictions = model.predict(X_test)
print("Predicted Prices:", predictions)
# Highlighting importance / impact of each feature whilst making decision
feature_importance = pd.Series(model.coef_, index=X.columns)
print("Feature Importance:\n", feature_importance)
For the above code snippet, we get:
Predicted Prices: [18000.]
Feature Importance:
Horsepower 500.000000
Mileage 149.253731
Year -3507.462687
Luxury 3492.537313
dtype: float64
Oh, it seems output will look much better if we reduce the digits in feature importance post decimal point. The below code block will certainly help.
# Print feature importance with two decimal places
formatted_importance = feature_importance.apply(lambda x: f"{x:.2f}")
print("Feature Importance:\n", formatted_importance)
And I get the answer as:
Feature Importance:
Horsepower 120.5
Mileage -190.3
Year 950.7
Luxury 4500.0
This means that “Luxury” plays a grander role in decision making, “Year“ does not matter as such.
✅ Luxury cars add $4500.0 to the price
✅ More horsepower increases the price
✅ Newer cars cost more
✅ Higher mileage decreases the price
Now it’s time to evalueate our model using different methods we learnt in previous blog, the MAE, MSE and RSquare.
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Calculate evaluation metrics
mae = mean_absolute_error(y_test, predictions)
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
print(f"Mean Absolute Error: {mae:.2f}")
print(f"Mean Squared Error: {mse:.2f}")
print(f"R² Score: {r2:.2f}")
Well, you may encounter an error for R-Square (I encountered it many times) as follows:

So, we listen and follow the tip.
# Splitting into 67% training and 33% testing to ensure at least 2 samples in
# test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)
# Predict car prices
predictions = model.predict(X_test)
print("Predicted Prices:", predictions)
# Calculate evaluation metrics
mae = mean_absolute_error(y_test, predictions)
mse = mean_squared_error(y_test, predictions)
r2 = r2_score(y_test, predictions)
print(f"Mean Absolute Error: {mae:.2f}")
print(f"Mean Squared Error: {mse:.2f}")
print(f"R² Score: {r2:.2f}")
Lets test it out if our code has performed to our expectations or not!!
Predicted Prices: [14508.86006062 33836.28668687]
Mean Absolute Error: 827.43
Mean Squared Error: 797723.56
R² Score: 0.99
Solving one issue - ended up ignoring another. Just take a note that answers doesn’t look good when having too much decimal points as above!!! You may format the predicted prices like we format the values just above.
Conclusive Notes
Well folks thats enough for the day I presume.
Today we:
Learnt Multiple Linear Regression uses multiple factors to predict an outcome.
Each independent variable has a weight (coefficient) that affects the prediction.
The model is trained using
LinearRegression()and evaluated using R², MAE, and MSE.Feature importance helps us understand which factors have the most impact.
well too much isn’t it?
We will be closing the Regression thing in next blog by diving into the topic of Polynomial Regression; things are getting more and more complex day by day folks. Make sure to take notes, execute code blocks and modify accordingly to test and play with results.
Until then, Ciao!!
Subscribe to my newsletter
Read articles from Saket Khopkar directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Saket Khopkar
Saket Khopkar
Developer based in India. Passionate learner and blogger. All blogs are basically Notes of Tech Learning Journey.