How Twitter (X)'s Birdwatch algorithm works

1. Introduction

In this blog, we try to understand Twitter (X)’s approach to fighting misinformation and polarization in users' opinions. The community notes feature in X uses a "bridging-based ranking" algorithm to identify and display context notes (like fact-checks) on potentially misleading content, prioritizing notes found helpful by users from diverse perspectives, rather than just the majority.

Source: Birdwatch: Crowd Wisdom and Bridging Algorithms can Inform Understanding and Reduce the Spread of Misinformation

Social media platforms unintentionally promote the formation of ideological groups. When users are exposed primarily to content that aligns with their existing beliefs, it creates echo chambers (you keep seeing the same type of reels on your feed that you like), reinforcing biases and leading to polarization. This environment makes it easy for misinformation to spread, as content favored by the dominant group is often amplified regardless of its accuracy. The challenge is to develop a system that evaluates the validity of news independently of user biases and group influence.

We start by understanding the foundation of the Birdwatch algorithm, which builds upon traditional recommendation systems. Many content platforms use matrix factorization to predict user preferences based on patterns in user–item interactions.

Interestingly, the same technology that powers content recommendations and user echo chamber formation—recommendation systems—can be adapted to tackle misinformation and polarization. Platforms like Netflix and Amazon have long used matrix factorization to suggest movies and products based on user preferences. We look at how tweaking these systems allow Birdwatch to create a more reliable and balanced post validation system.

Then we dive deep into the Birdwatch algorithm and explore the details of how it works.

2. Background: Recommendation Systems and matrix factorisation

Recommendation systems are a type of information filtering system that attempts to predict the "rating" or "preference" that a user would assign to an item.

Items: The entities a system recommends. For the Google Play store, the items are apps to install. For YouTube, the items are videos.

One common architecture for recommendation systems consists of the following components:

Candidate generation
Scoring
Re-ranking

Candidate generation

Candidate generation is the first stage of recommendation. Given a query, the system generates a set of relevant candidates. The following table shows two common candidate generation approaches:

Type	Definition	Example
Content-based filtering	Uses similarity between items to recommend items similar to what the user likes.	If user A watches two cute cat videos, then the system can recommend cute animal videos to that user.
Collaborative filtering	Uses similarities between queries and items simultaneously to provide recommendations.	If user A is similar to user B, and user B likes video 1, then the system can recommend video 1 to user A (even if user A hasn’t seen any videos similar to video 1).

Collaborative filtering finds hidden patterns and adjusts to new trends by using user behavior, making it more flexible and adaptable than content-based filtering, which only uses item features. We will mainly focus on collaborative filtering using matrix factorization.

Matrix factorization is a simple embedding model. Given the feedback matrix $A \in \mathbb{R}_{m \times n}$

where m is the number of users (or queries) and n is the number of items, the model learns:

A user embedding matrix $U \in \mathbb{R}_{m \times d}$, where row $i$ is the embedding for user $i$
An item embedding matrix $V \in \mathbb{R}_{n \times d}$ where row $j$ is the embedding for item $j$

The embeddings are learned such that the product $UV^T$ is a good approximation of the feedback matrix $A$. Observe that the $(i,j)$ entry of $UV^T$ is simply the dot product $\langle U_i, V_j \rangle$ of the embeddings of user $i$ and item $j$ which you want to be close to $A_{ij}$.

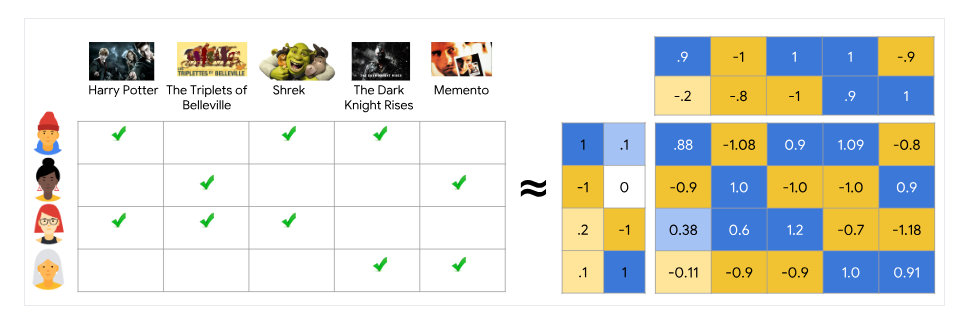
source: https://developers.google.com/machine-learning/recommendation/collaborative/matrix

The Basic Model

The core idea is to represent each user $u$ with a latent vector $\mathbf{p}_u \in \mathbb{R}^K $ and each item $i$ with a latent vector $\mathbf{q}_i \in \mathbb{R}^K$ . The predicted rating $\hat{r}_{ui}$ is computed as the dot product of these two vectors:

$$\hat{r_{ui}} = p_u ⋅ q_i$$

Incorporating Biases

To capture systematic tendencies (for example, some users rate higher on average, or some items are generally more popular), a baseline predictor is often added:

$\hat{r_{ui}} = μ +b_u + b_i + p_u.q_i$.

Where:
- $\mu$ is the global average rating.
- $b_u$ is the user bias (how much user $ u $ 's ratings deviate from the average).
- $b_i$ is the item bias (how much item $ i $ 's ratings deviate from the average).

Optimization Objective

The model parameters $\Theta = {{\mu, b_u, b_i, \mathbf{p}_u, \mathbf{q}_i\\}}$ are learned by minimizing the regularized squared error over all observed ratings:

$$\min_{\Theta} \sum_{(u,i) \in K} (r_{ui} - \hat{r}_{ui})^2 + \lambda (b_u^2 + b_i^2 + \|\mathbf{p}_u\|^2 + \|\mathbf{q}_i\|^2)$$

Here:
- $\mathcal{K}$ is the set of observed (non-null) ratings.
- $\lambda$ is a regularization parameter that helps prevent overfitting by penalizing large values in the parameters.

Learning via Gradient Descent

Typically, stochastic gradient descent (SGD) is used to iteratively update the parameters. For an observed rating $r_{ui}$ , define the prediction error:

$e_{ui}=r_{ui}−(μ+b_u+b_i+p_u⋅q_i)$
Then the updates for a learning rate $\eta$ are:

$$\begin{aligned} &\text{- Global bias:} \quad \mu \leftarrow \mu + \eta (e_{ui} - \lambda \mu) \\ &\text{- User bias:} \quad b_u \leftarrow b_u + \eta (e_{ui} - \lambda b_u) \\ &\text{- Item bias:} \quad b_i \leftarrow b_i + \eta (e_{ui} - \lambda b_i) \\ &\text{- User latent vector:} \quad p_u \leftarrow p_u + \eta (e_{ui} q_i - \lambda p_u) \\ &\text{- Item latent vector:} \quad q_i \leftarrow q_i + \eta (e_{ui} p_u - \lambda q_i) \end{aligned}$$

This iterative process is repeated until the model converges or a predetermined number of iterations is reached.

3. Tweaking Recommendation Systems to Address Misinformation

"Within every adversity lies the seed of equal or greater benefit." – Napoleon Hill

Birdwatch builds on matrix factorization(discussed above) to gather user opinions about the truthfulness of news. Instead of just predicting what users like, it adds ways to manage binary voting, credibility weighting, and polarization.

Magic lies in $i_n$

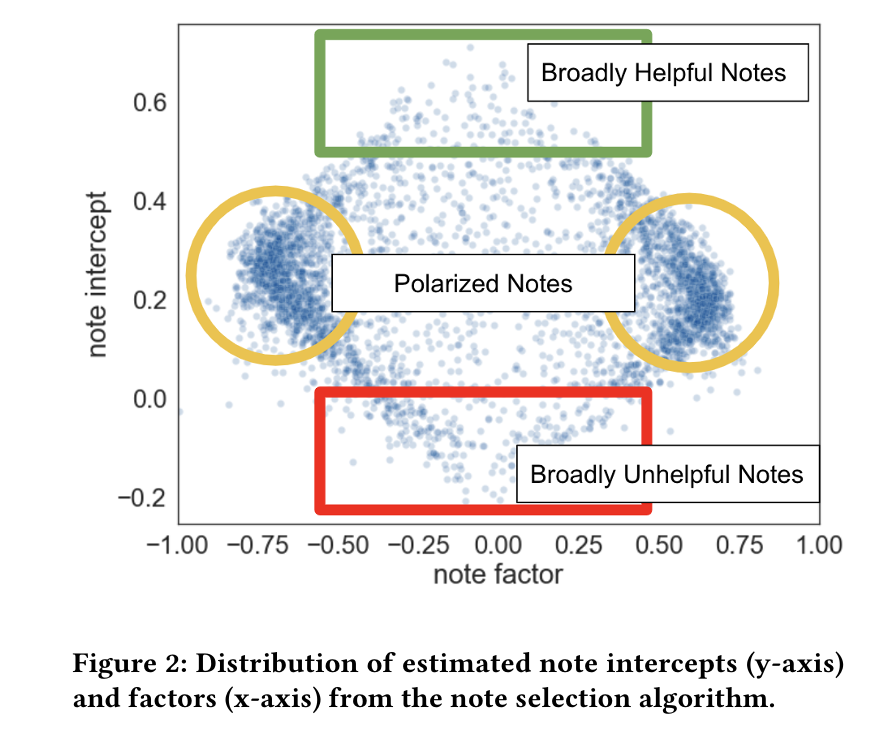
In the birdwatch algorithm, the representation space identifies whether notes may appeal to raters with specific viewpoints. By controlling this, we are able to identify notes that are more broadly appealing than might be expected given the viewpoint of the note and its raters. In particular, we predict each rating as:

$$r_{un}=μ+i_u+i_n+f_u⋅f_n$$

where the prediction is the dot product of the user and notes' vectors $f_u$ and $f_n$ , added to the sum of three intercept terms:

- $\mu$ is a global intercept term, accounting for an overall tendency of raters to rate notes as “helpful” vs. “not helpful.”

- $i_u$ is the user’s intercept term, accounting for a user’s leniency in rating notes as “helpful.”

- $i_n$ is the note’s intercept term, capturing the characteristic "helpfulness" of the note beyond what can be explained by rater viewpoints and leniency. This note intercept term, $i_n$ , is used to assign a single global score to a note in birdwatch, This is where the algorithm differs from traditional recommender system algorithms that personalize content.

Balancing Precision and Recall in Birdwatch

Birdwatch prioritizes precision (minimizing false positives) over recall (minimizing false negatives) to protect the platform's integrity by reducing the visibility of low-quality notes. To achieve this, it applies stronger regularization on the intercept terms $(i_u, i_n, \mu)$ compared to the latent factors $(f_u, f_n)$. This forces the model to rely more on user and note factor vectors to explain rating variation before adjusting with intercepts. As a result, for a note to achieve a high intercept value, it must be rated helpful by raters with diverse factor profiles. The model parameters are estimated by minimizing the following regularized least squares loss using gradient descent:

$$\min_{\{i, f, \mu\}} \sum_{r_{un}} (r_{un} - \hat{r}_{un})^2 + \lambda_i (i_u^2 + i_n^2 + \mu^2) + \lambda_f (\|\mathbf{f}_u\|^2 + \|\mathbf{f}_n\|^2)$$

Where $\lambda_i$(0.15), the regularization on the intercept terms, is currently 5 times higher than $\lambda_f$(0.03), the regularization on the factors.

This setup ensures that the latent factors handle most of the explanatory burden, promoting better generalization and reducing overfitting to individual biases.

Moreover,

the algorithm is different from general MF in how it deals with hidden features of user preferences. Birdwatch uses continuous latent factors to capture a range of opinions.

4. The Birdwatch Algorithm

In our approach, the representation space identifies whether notes may appeal to raters with specific viewpoints, and as a result we are able to identify notes with broad appeal across viewpoints.

The matrix factorization is re-trained from scratch every hour, Additional logic is added to detect if the loss is more than expected (currently by detecting if the loss is above a hard threshold of 0.09) that may have resulted from an unlucky initialization and local mode, and then re-fit the model if so. Before understanding the algorithm, we must first understand two terms: “Rater Helpfulness Score” and “Multiple Scorers”.

Rater Helpfulness Score

The Rater Helpfulness Score shows how closely a contributor's ratings match the ratings on notes that are labeled as “Helpful” or "Not Helpful” (showing a clear agreement among raters, and not marked as “Needs More Ratings”).

$$\frac{s - (10 \cdot h)}{t}$$

where:

$s$\= Number of successful valid ratings (ratings that matched the final note status).
$−10⋅h$ = Penalty (10 points per note) for rating a note as helpful when it had an extremely high Tag-Consensus Harassment-Abuse Note Score.
$t$ = Total number of valid ratings made.

Multiple scorers:

The matrix factorization is applied several times to analyze notes from different perspectives. In the end, the results from all the scorers are combined to produce the final outcome.

Scorer	Definition
Core	Baseline model using matrix factorization on all ratings.
CoreWithTopics	Core model with topic-based rating segmentation.
Expansion	Includes more raters and notes for broader coverage.
ExpansionPlus	Enhanced Expansion with time trends and rater reputation.
Group	Applies matrix factorization separately for user groups.
Topic	Analyzes ratings within specific subject areas.

Complete Algorithm Steps:

Prescoring

Pre-filter the data: to address sparsity issues, only raters with at least 10 ratings and notes with at least 5 ratings are included (done only once, not recursively). Combine ratings made by raters with high post-selection-similarity.
For each scorer (Core, CoreWithTopics, Expansion, ExpansionPlus, and multiple Group and Topic scorers):
- Fit matrix factorization model, then assign intermediate note status labels for notes whose intercept terms (scores) are above or below thresholds.
  
  Criteria for a helpful note:
  
  $i_n > 0.4$ : a greater overall rating beyond what can be explained by rater viewpoint
  
  $|f_n| < 0.5$ : notes marked as "Helpful" must have broad and diverse support. (fₙ represents latent factors capturing nuanced variations in how different groups of raters perceive the note.)
- Compute Author and Rater Helpfulness Scores based on the results of the first matrix factorization, then filter out raters with low helpfulness scores from the ratings data.
- Fit the harassment-abuse tag-consensus matrix factorization model on the helpfulness-score filtered ratings, then update Author and Rater Helpfulness scores using the output of the tag-consensus model.(another matrix factorization model for the harassment and abuse tag: more info)

Scoring

Load the output of step 2 above from prescoring, but re-run step of pre-filtering on the newest available notes and ratings data.
For each scorer (Core, CoreWithTopics, Expansion, ExpansionPlus, and multiple Group and Topic scorers):
- Re-fit the matrix factorization model on ratings data that’s been filtered by user helpfulness scores in initial step of scoring.
- Fit the note diligence matrix factorization model. This is a similar matrix factorization model used to identify notes that people with different viewpoints find True.
- Calculate the upper and lower confidence limits for each note's intercept $(i_n)$ by adding pseudo-ratings and then re-fitting the model with these ratings. (see Modeling Uncertainty)
Reconcile scoring results from each scorer to generate final status for each note.
Update status labels for any notes written within the last two weeks based the intercept terms (scores) and rating tags. Stabilize helpfulness status for any notes older than two weeks.
Assign the top two explanation tags that match the note’s final status label or if two such tags don’t exist, then revert the note status label to “Needs More Ratings”.

Modeling Uncertainty

While the matrix factorization approach above has many nice properties, it doesn't give us a natural built-in way to estimate the uncertainty of its parameters. We take two approaches to model uncertainty:

Pseudo-rating sensitivity analysis

We introduce "extreme" ratings from "pseudo-raters" to the model. These ratings include both helpful and not-helpful scores. We also consider a factor of 0, as it can significantly affect note intercepts.
After adding all possible pseudo-ratings, we calculate the maximum and minimum values for each note's intercept and factor parameters. (This method is similar to using pseudocounts in Bayesian modeling or Shapley values.)
A note is labeled "Not Helpful" if the maximum (upper confidence bound) of its intercept is less than -0.04. This is in addition to the rules on raw intercept values mentioned earlier.

Supervised confidence modeling

We also employ a supervised model to detect low confidence matrix factorization results. If the model predicts that a note will lose Helpful status, then the note will remain in Needs More Ratings status for up to an additional 180 minutes or until the supervised model predicts the note will remain rated Helpful.The maximum effect of the supervised model is no more than a 180 minute delay, and all notes will receive a minimum 30 minute delay to gather additional ratings. This helps reduce notes briefly showing and then returning to Needs More Rating status.

5. References and Further Reading

While writing this blog, I attempted to implement a basic version of the Birdwatch matrix factorization to determine the validity of news based on user diversity in my gamified news platform project. You can check it out here: link

The complete source code of Birdwatch (now Community Notes) is open source. You can find it here: link