Asymmetric cryptography/Public Key encryption

Let’s say Alice, as expected, wants to send a secret message to Bob on the public channel. Bob, at the same time, has the lock with her own (private) key that won’t be transmitted to anybody. So, Bob initially sends her lock to Alice. Alice simply puts the message into the box and locks the box with the received lock. She just clicks on the lock, and the box is protected. Now it is safe to send back the box to Bob. He could then unlock the box with her private key, and the mission is completed.

The analogy to the public key cryptography is clear. Alice just requests Bob’s public key and encrypts the message. Bob then uses the private key to decrypt it. That’s all the analogy.

However, at a later glance, the lyric description above does not apply to message signing. In the case of the signing, the message is not hidden; it is readable. Only the integrity and authenticity of the message is ensured.

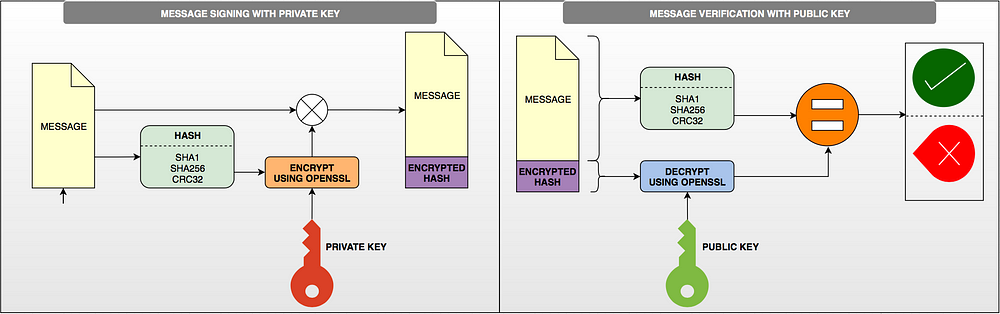
The receiving side gets the message with its signature and tries to produce the same signature using a publicly available, shared key. Assume sign(message, public key)= new signature. If the signatures are the same, the message considered authenticated.

Let’s take JWT as an example and use RSA25. How does it work?

The name briefly explains the steps used: RSA256 = SHA-256 + RSA. At the first step, the sender side calculates the hash of the JWT payload with the SHA-256 hash algorithm. The result is a 256-bit size hash. At the next step, the hash is encrypted with the private key using PKCS1 v1.5 padding.

The result of this encryption is called the signature and is sent in the JWT in the third part of JWT.

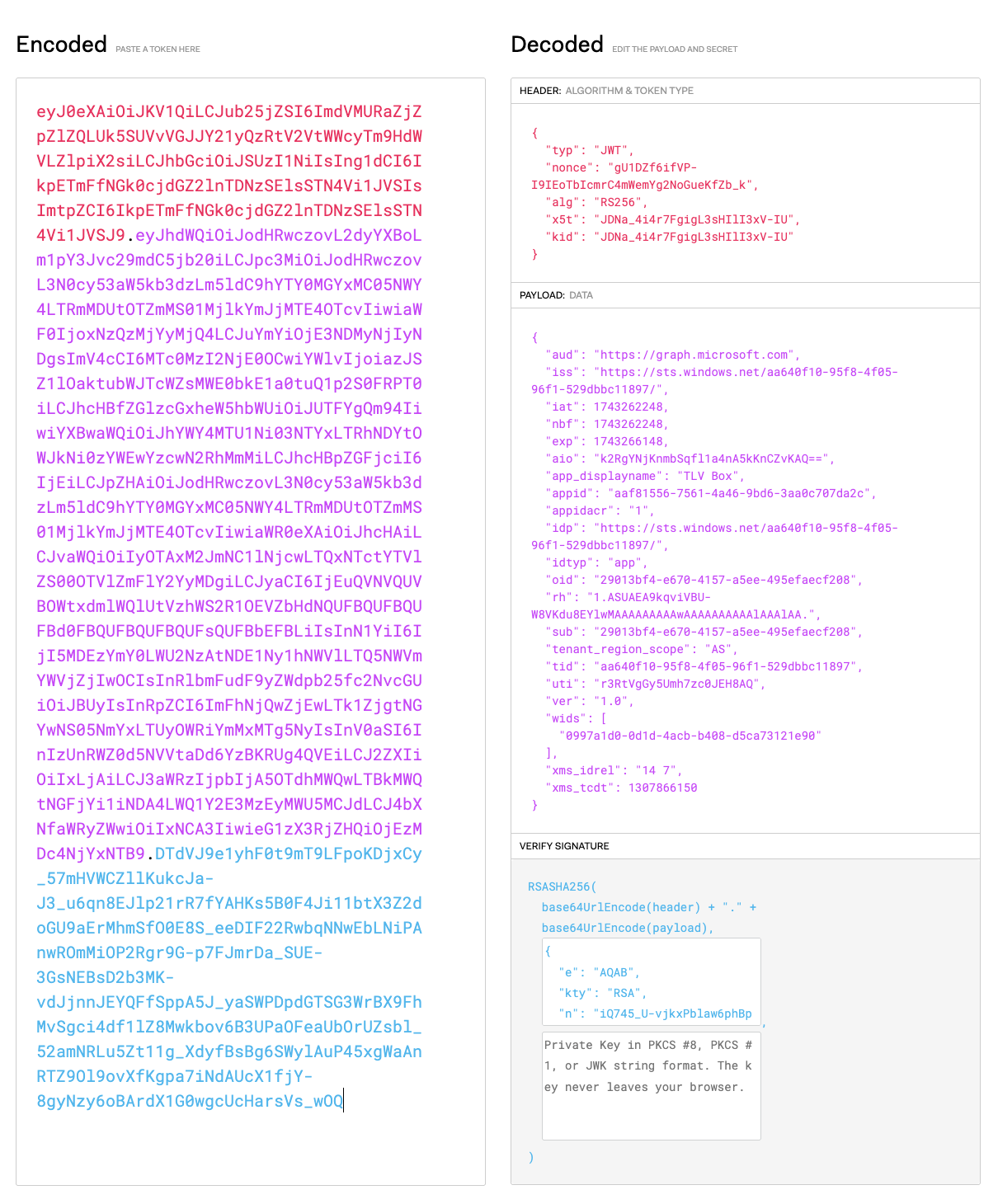
The receiving side just performs the reverse operations. First, it splits the received JWT into three parts. At the snapshot above, these parts are colored at with different tints. The middle part of the JWT is parsed as JSON, and “iss” (issuer) claim is processed. The most common processing is just to compare its value to some pre-defined and trusted one. Any other values should be rejected. If the comparison matches, the value of this claim is concatenated with “.well-known/openid-configuration” string to issue the request to this address (called discovery endpoint) to get JSON Web Key Set (KWKS) from its “jwks_url” response’s item. For example, the “iss” claim “https://sts.windows.net/aa640f10-95f8-4f05-96f1-529dbbc11897/” becomes “https://sts.windows.net/aa640f10-95f8-4f05-96f1-529dbbc11897/.well-known/openid-configuration“. Click the last link to see how the response of the discovery endpoint looks like.

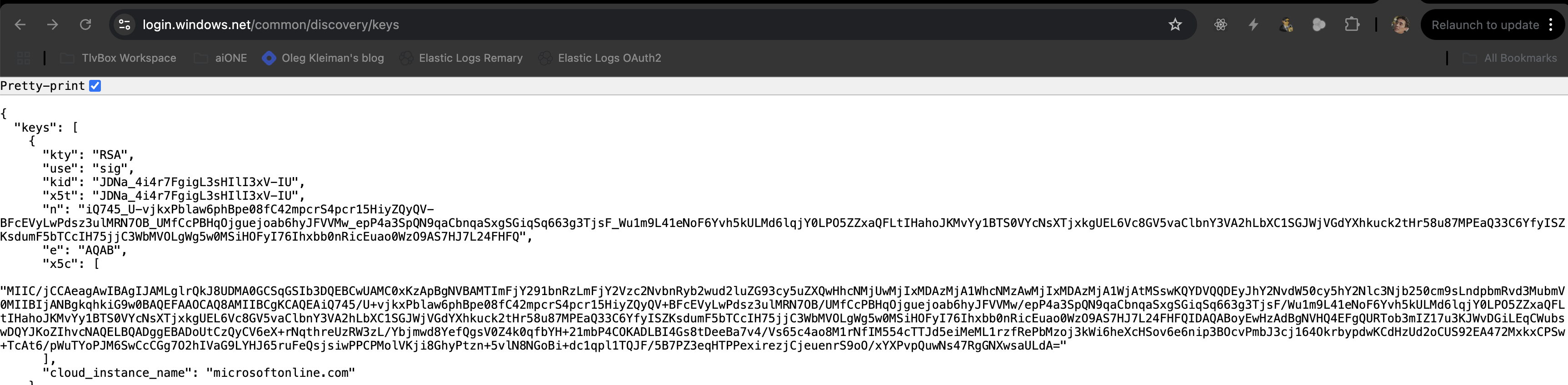
Anyway, from there the receiver side obtains the public key. It comes in the form of n and e pair (see later). Now the receiver tries to restore the signature from the last part of the received JWT: firstly, it starts with hashing the JWT payload by SHA-256 and encrypts the computed hash with obtained public key. This way the calculated signature is calculated and now it could be compared to signature passed in the JWT. If the signatures match, the token considered valid.

Now it’s time to talk about the RSA in this process. The algorithm itself starts with finding two random large prime numbers p and q to calculate the product n = q X q. This n is used as the modulus for both private and public keys. It is the heart of the process that is based on the difficulty of factoring large numbers, meaning that finding the original p and q is infeasible for large numbers (e.g., 2048-bit modulus). Initially, we need to calculate the count of positive integers less than n which are relatively prime to n. This is what Euler’s Totient Function is used for:

$$\phi(n) = (p-1) * (q-1)$$

Now define:

1. e - public exponent, used for encryption, hence its name - as coprime to this number. A common choice is one of the firsts the Fermat numbers:

$$F_n = 2^{2^n} +1$$

i.e. {3,5,17,257,65537}, because these numbers consist of a relatively small number of ones in their binary form, which is essential for using later exponentiation by squaring. Fermat numbers are occasionally the primes. Often 65537 is chosen for efficiency. This is usually stored in base64 as AQAB

printf '%06x' 65537 | xxd -r -p | base64

2. Define d - the private exponent - as solving:

$$d \times e = 1\mod{\phi(N)}$$

Usually, d is computed using the Extended Euclidean Algorithm.

3. Now define the public key as the pair of (e, n) and the private key as the pair of (d, n).

4. To re-create the signature at the receiver side, the RSA algorithm takes the message m (previously produced 256-bit size hash) and firstly converts it into a cipher-text c using the public key n. Thus, it calculates:

$$c = m^e \pmod{n}$$

This calculation can be done reasonable quickly, even for very large numbers, using the exponentiation by squaring (especially with Right-To-Left Binary Method). The algorithm of such exponentiation is amazingly simple:

$$x^n={\begin{cases}x,&{\mbox{if }}n{\mbox{ = 1}}\\(x^{2})^{n/2},&{\mbox{if }}n{\mbox{ is even}}\\x\times (x^{2})^{(n-1)/2},&{\mbox{if }}n>{\mbox{2 is odd}}\end{cases}}$$

The step 4 is now completed. We have the calculated signature on the receiver side. The remaining step is to validate this value against the signature sent with JWT.

4. To validate the signature, obtain d and firstly compute the hash of the original message M

$$H = SHA-256(M)$$

Now convert S (the received signature back to a message hash:

$$H' = S^d \pmod N$$

Compare H’ and H to conclude the authenticity of the message.