Since these are basic school-level math concepts, I won't go into detail. I will simply show how they are used in data science. Thank you!

Inverse Function

An inverse of a function is a function that reverses the effect of the original function.

If you have a function f that maps an element x from set X to an element y in a set Y, the inverse function f^(-1) map y back to x.

Given a function f: X → Y, then inverse function f^(-1): y → x

The inverse function f^(-1) satisfies the following condition:

1. for all x∈X: f(f^-1(y)) = y

2. for all y∈Y: f^-1(f(x)) = x

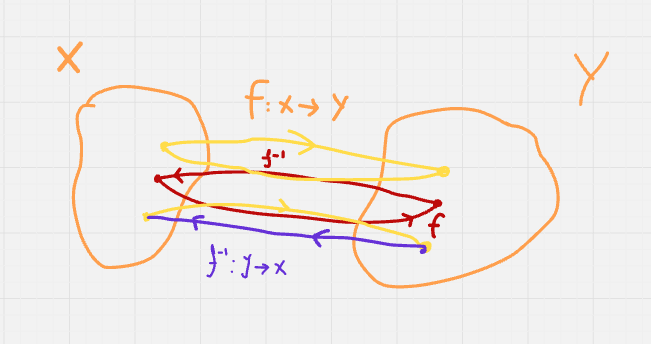
These conditions imply that applying the function and then it inverses will return the origin one.

Identity function:

I: X → x => I(a) = a

Properties of identity function:

1. Preservation: The identity function does not change any element. You will get the same element after performing the dot product. If x is in the domain, then the image of x under the identity function is x itself.

2. Linearity: The identity function is a linear transformation.

   • I(u + v) = I(u) + I(v)

   • I(cu) = cI(u) = cu

3. Identity matrix: An n x n matrix where all the diagonal elements are 1, and all other elements are 0.

4. Inverse: The identity function is its own inverse. A function f has an inverse if and only if it is bijective.

   • Injective (one-to-one): Different elements in the domain map to different elements in the codomain.

   • Surjective (onto): Every element in the codomain is the image of at least one element in the domain.

5. Find the inverse: y = 2x+3 for x:

   y = 2x+3

   y-3 = 2x

   x = (y-3)/2

   The inverse function, f-1(y) = (y-3)/2

   Verification:

   

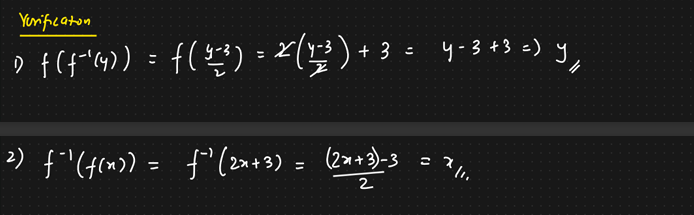
Application of function and inverse function

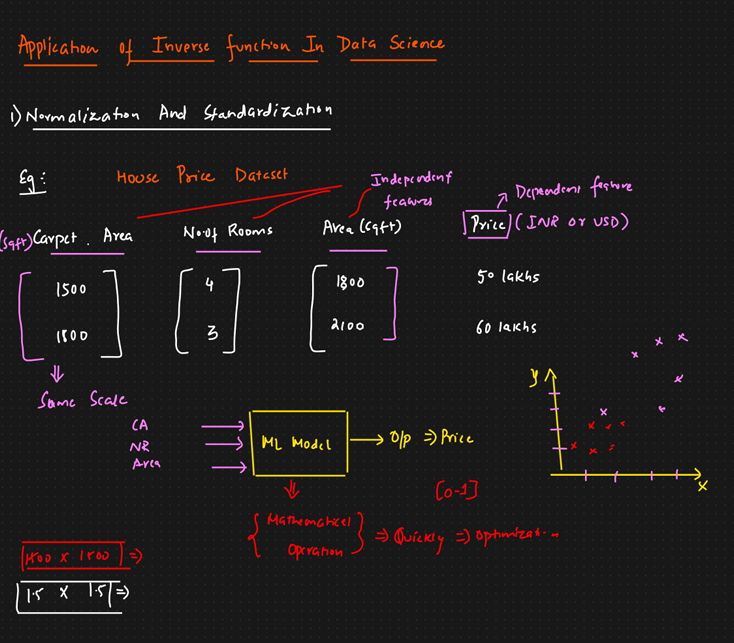
Standardization:

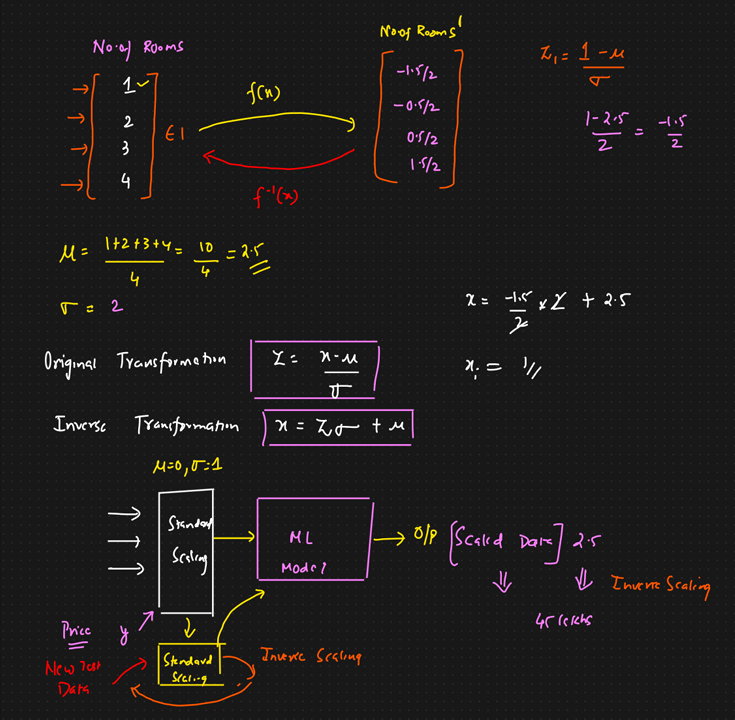
Normalization:

• min(x) checks for the x features

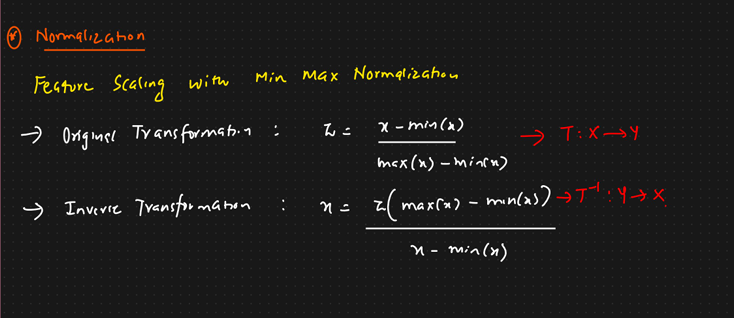
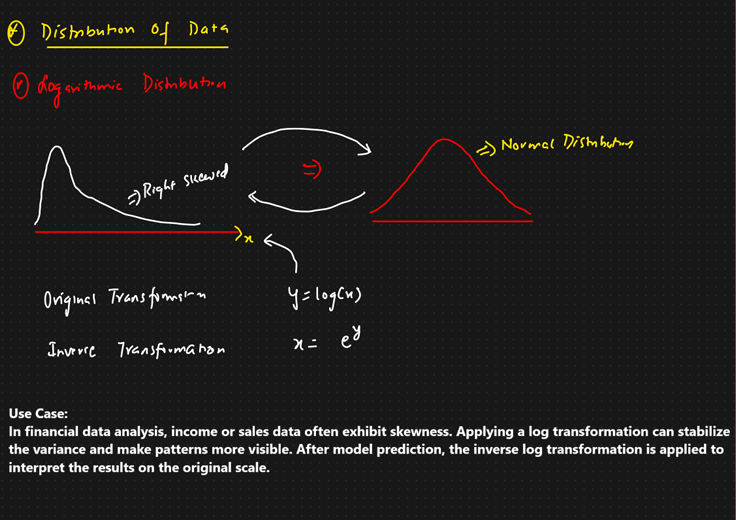
How to find inverse of a matrix

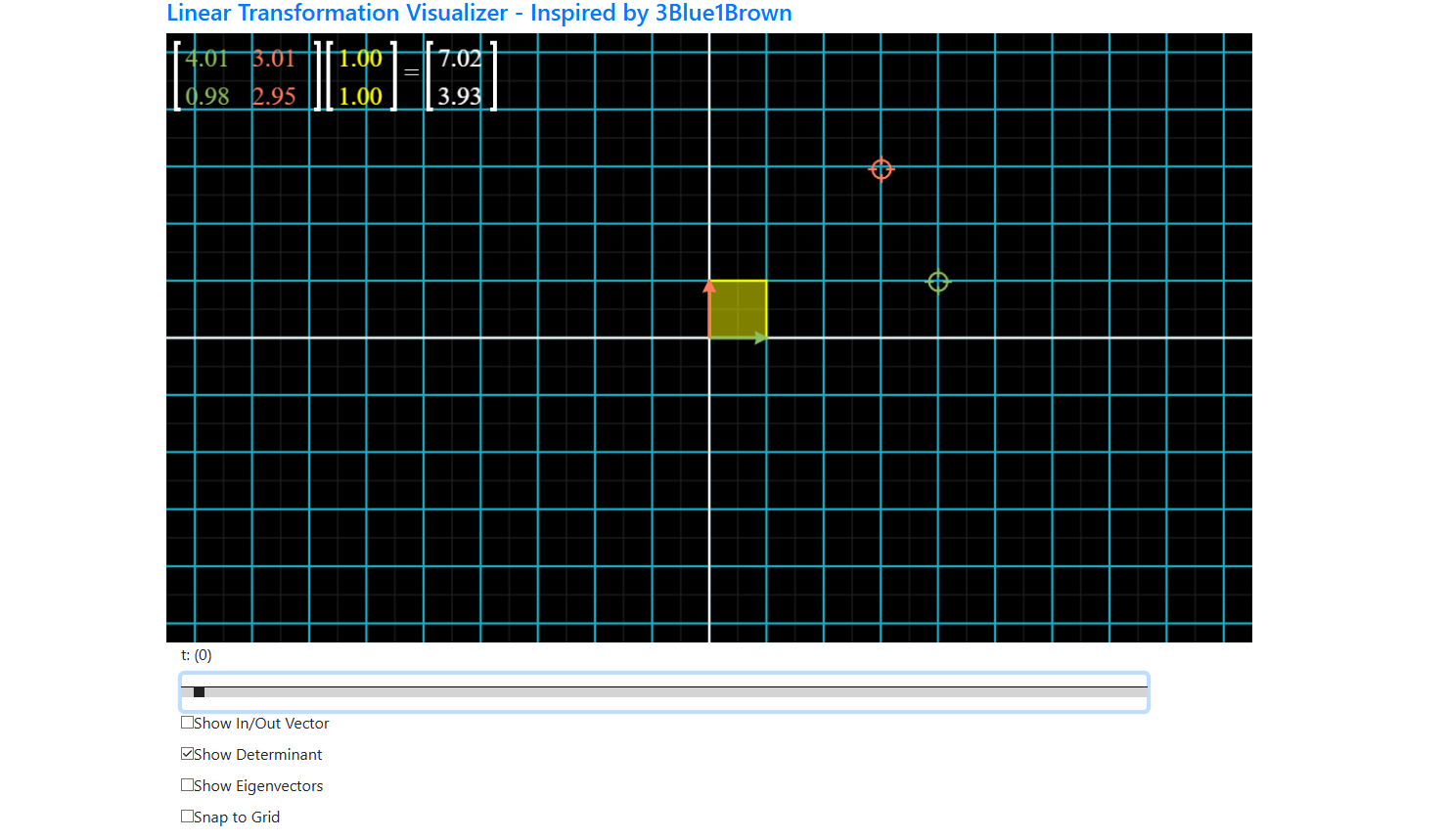
When we scale these unit vectors to the red and green points, the entire unit vector will scale to that point. Linear transformation is all about this: if I have a specific point and want to transform it to another vector, scaling will keep my origin the same, but the lines will stretch until they reach that particular point.

Now - what does determinant actual mean?

Look at the below shaded area. This area has been created after scaling. This is called a linear transformation itself. I hope you are able to understand that the determinant is basically the shaded linear transformed area.

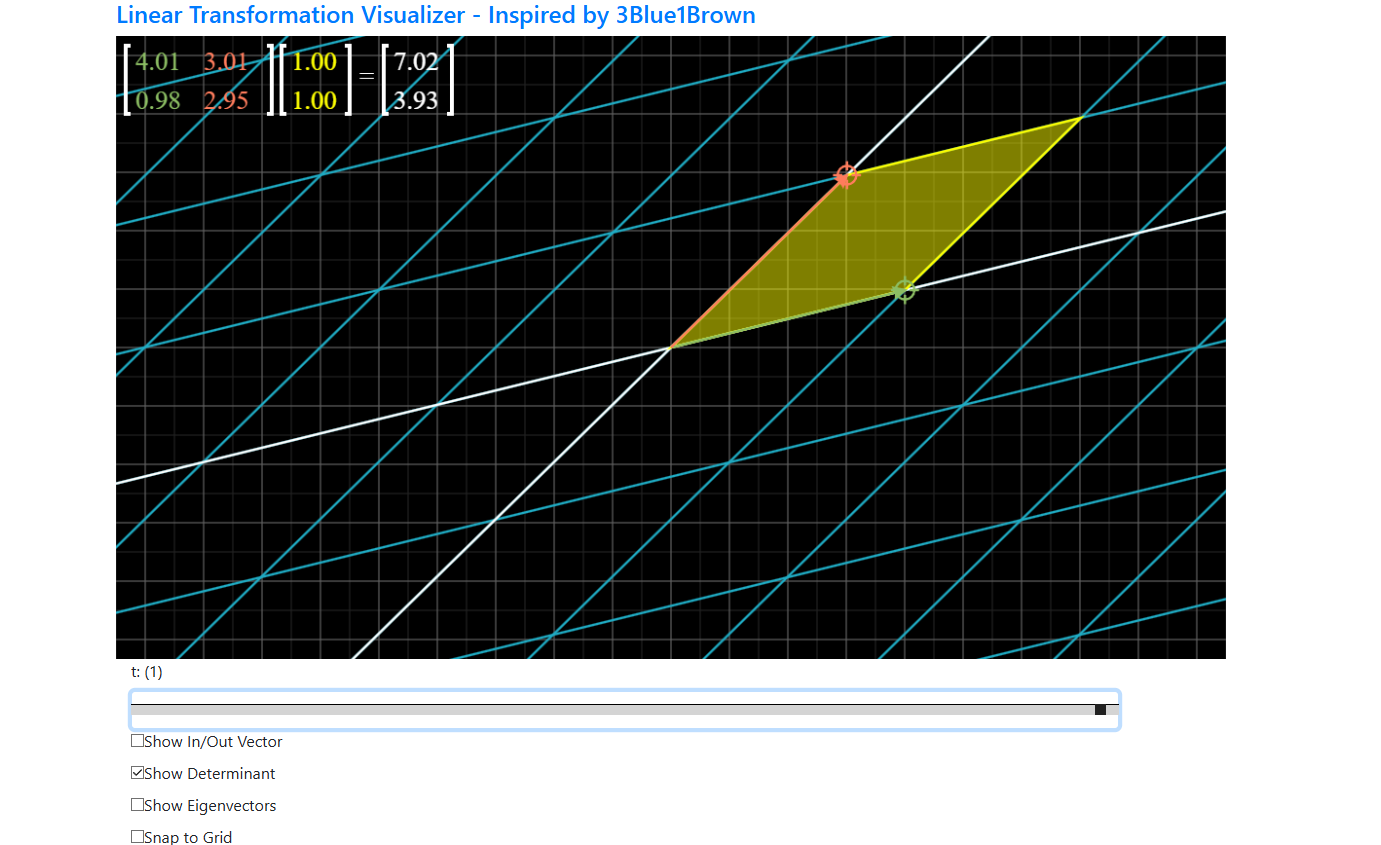
Now we will find the inverse of A

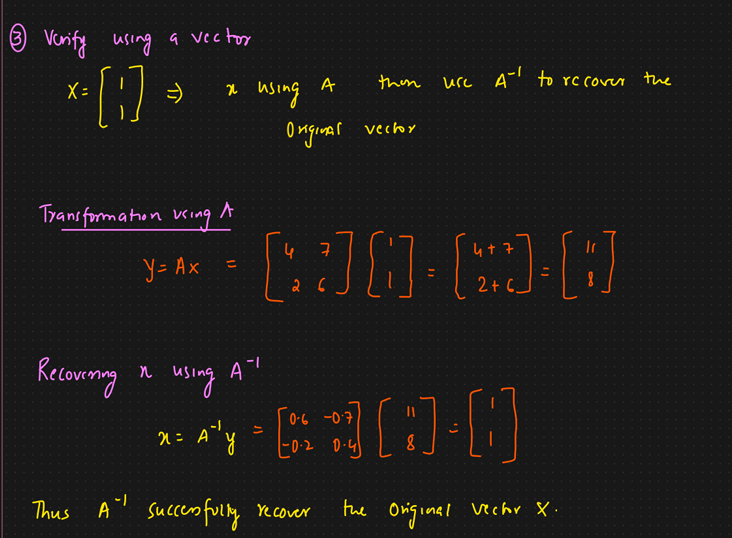
This is it!