Big O Notation Explained, Part 1: The Basics
 Pablo Albian
Pablo Albian
If you're a software engineer, you've probably heard about Big O notation—at least while learning about algorithms or preparing for job interviews at top tech companies (FAANG and similar). But without a formal Computer Science degree or a math background, it’s easy to feel overwhelmed by terms like logarithmic time or space and time complexity.
Don’t worry—it's not as hard as it sounds. With a bit of curiosity and focus, you'll be able to master it just by reading approachable explanations like this one and applying them to algorithmic problems (think Leetcode-style challenges).
Is learning Big O Notation worth it?
It is, absolutely.
Most of content online is heavily focused on FAANG-style interviewing. There' is a widespread believe that there is no benefit beyond that, but there are multiple benefits in learning Big O Notation if you aim to become a solid software engineer:
Big O gives you a language to reason about performance. Learning to avoid things like O(n²), when possible, means the difference between something that scales and something that breaks.
Today, with the help of AI, virtually anyone can code. But thinking on terms of complexity helps you write clean and scalable code, and it’s what sets great engineers apart.
Your logical thinking will improve. You’ll start to enjoy solving complex problems, and coding will become more intuitive and fun.
Understanding Big O
Big O measures how efficient your code runs in terms of time (and sometimes memory) as the input size increases.
Let’s look at a simple example:
public void processList(List<String> list) {
for (int i = 0; i <= list.size(), i++) {
processElement(list[i]);
}
}
Let’s say that the ‘processElement’ method contains some logic that takes exactly one second to run. How does the method’s runtime change as the list grows?
| List size | Time (seconds) |
| 1 | 1 |
| 2 | 2 |
| 1000 | 1000 |
| n | n |
So if the list has n elements, we run the process n times. This is linear time, or O(n). The runtime grows in direct proportion to the input size:
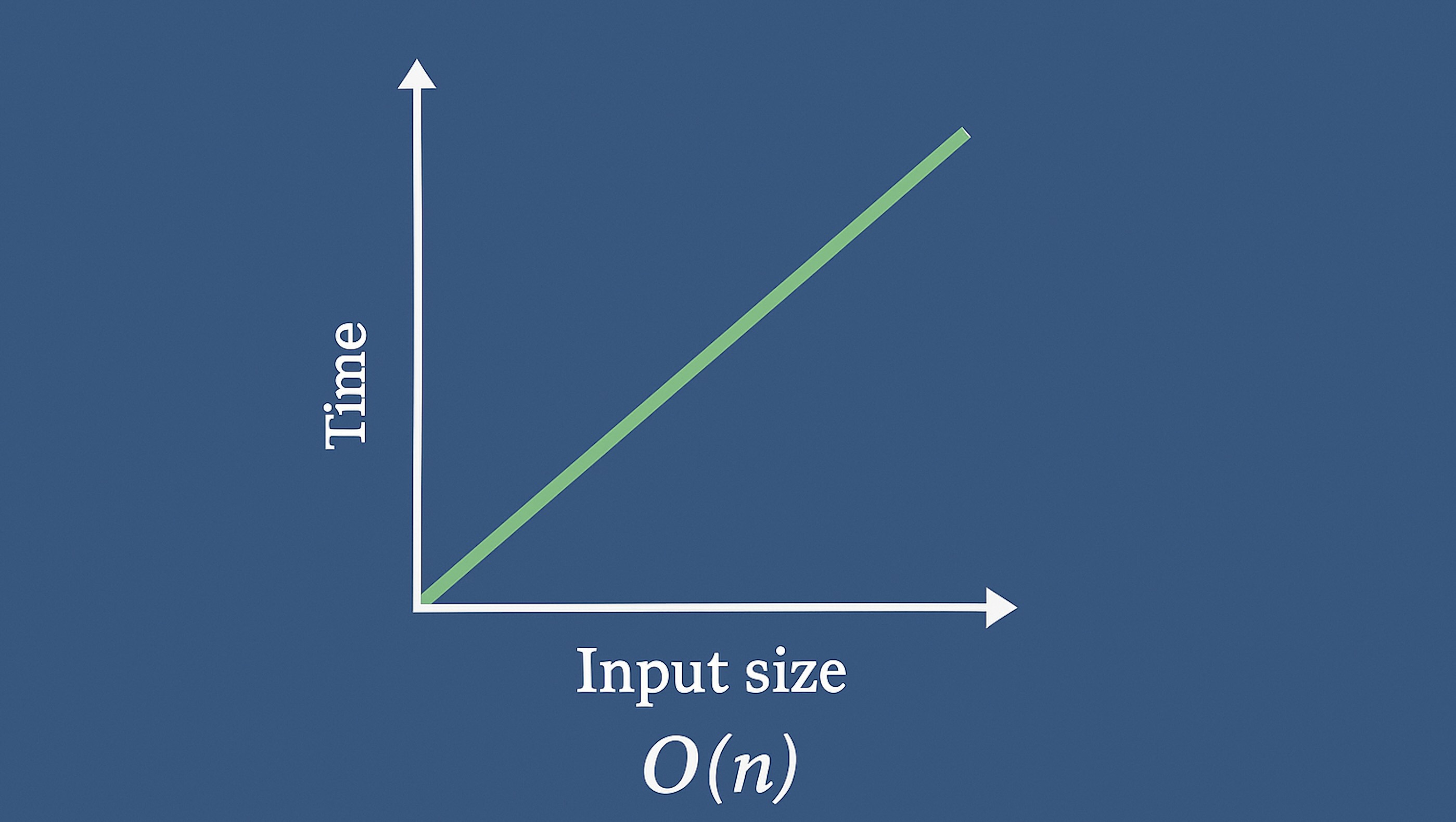
Common Big O Complexities
These are the common Big O complexity levels, ordered from fastest to slowest:
O(1) – Constant time
O(log n) – Halves input each step
O(n) – Grows linearly with input
O(n log n) – Linear + logarithmic growth
O(n²) – Nested loops over input
O(n³) – Triple nested loops
O(2ⁿ) – Doubles with each input
O(n!) – All permutations of input
In the next entry, we’ll look at short code examples for each of these complexities. Can you guess how they might look?
Subscribe to my newsletter
Read articles from Pablo Albian directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
