Back in 1997, the U.S. National Institute of Standards and Technology (NIST) launched a global competition to find the next generation encryption standard. After years of rigorous testing and analysis, an algorithm called Rijndael emerged victorious, becoming what we now know as AES. Today, AES is everywhere, securing hard drives, protecting internet communications, and even built directly into the processors of our computers, phones, and countless other devices. But beneath this ubiquity lies an elegant cryptographic dance of confusion and diffusion that transforms our readable data into seemingly random gibberish that only the intended recipient can decipher. In this post, we'll journey into the inner workings of AES, demystifying the core principles that make it the backbone of modern digital security. Whether you're a cybersecurity enthusiast or simply curious about how your information stays private in an increasingly connected world, understanding AES offers a fascinating glimpse into the mathematics that powers our digital trust.

The Basics of Encryption

At its core, encryption is about transforming information (called plaintext) into an unreadable format (called ciphertext) using a secret key. Only someone with access to that key should be able to convert the ciphertext back into the original plaintext.

In the digital world, plaintext, ciphertext, and keys are all represented as sequences of bits—just strings of 0s and 1s. A good encryption algorithm creates ciphertext that appears completely random to anyone without the key.

One of the simplest encryption methods is the exclusive-or (XOR) operation, where each bit of the plaintext is combined with the corresponding bit of the key. If the key bit is 1, we flip the plaintext bit; if the key bit is 0, we leave it unchanged. This method is perfectly secure—but only if you never reuse the key. This limitation makes it impractical for everyday use where we need to encrypt large amounts of data or multiple messages with the same key.

XOR Encryption: A Simple but Limited Approach

Before working with advanced encryption methods like AES, let's work with basic XOR encryption, one of the simplest forms of data encryption. While XOR encryption is easy to understand and implement, it is not robust at all for securing sensitive data in real-world applications.

XOR encryption uses the exclusive OR (XOR) logical operation to encrypt data. In the XOR method, each bit of the plaintext is combined with a corresponding bit from the key using the XOR operator. The result is ciphertext that appears scrambled and unreadable.

Properties of XOR

Reversible: Applying XOR twice with the same key retrieves the original data.

$$A \oplus K \oplus K = A$$

Where A is plaintext and K is the key.

Simplicity: It is Easy to implement with minimal computational overhead.

Here’s a step-by-step explanation:

Plaintext: Start with readable data, e.g., "HELLO".
Key: Choose a secret key, e.g., "KEY".
XOR Operation: Convert both plaintext and key into binary, then apply the XOR bit-by-bit.
Ciphertext: The result is encrypted data that looks unintelligible.

Plaintext ("HELLO"): Binary representation = 01001000 01000101 01001100 01001100 01001111
Key ("KEY"): Binary representation = 01001011 01000101 01011001

$$01001000 \oplus 01001011 = 00000011$$

$$ 01000101 \oplus 01000101 = 00000000$$

$$ 01001100 \oplus 01011001 = 00010101$$

The resulting ciphertext in binary is scrambled and unreadable.

To decrypt, apply the XOR again with the same key:

Ciphertext ⊕ Key = Original Plaintext.

While XOR encryption demonstrates the basic principles of cryptography, it has significant limitations.

If the same key is reused across multiple messages, attackers can exploit patterns and recover plaintext. If two ciphertexts are XORed together (C1⊕C2), it cancels out the key and reveals information about both plaintexts. The key must be as long as the plaintext for optimal security (as in a one-time pad). Short keys lead to predictable results. XOR lacks additional layers of security like substitutions or permutations, found in advanced algorithms like AES. Also, with a short key length, attackers can easily try all possible keys to decrypt the ciphertext.

AES as a Block Cipher

Okay, before we jump into the specifics of AES's inner workings, let's define two fundamental concepts that are crucial to understanding AES: Block Ciphers and the State.

There are primarily 2 types of ciphers:

Stream Ciphers: Stream ciphers encrypt data one bit or byte at a time. Imagine a flowing stream of data where each element is encrypted individually.
Block Ciphers: Block ciphers, on the other hand, divide the plaintext into fixed-size blocks and encrypt each block as a single unit.

AES is classified as a block cipher, meaning it operates on fixed-size blocks of data—specifically, 128 bits (16 bytes) at a time. These 16 bytes are arranged in a 4×4 grid called the "state," which is transformed through multiple rounds of operations.

If the data is larger than 16 bytes (which it almost always is), it gets divided into multiple blocks, each processed separately. How these blocks connect to each other is determined by various "modes of operation" like CBC (Cipher Block Chaining) or GCM (Galois/Counter Mode). We’ll implement CBC in this paper.

The State: AES's Working Canvas

The state in AES is an intermediate representation of the data being encrypted or decrypted. You can think of it as the "canvas" on which AES performs its transformations. The state is a 4x4 matrix of bytes. Since AES operates on 128-bit blocks (16 bytes), these 16 bytes are arranged into this 4x4 matrix.

$$\text{State} = \begin{bmatrix} a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} \\ a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix}$$

The 128-bit input block is copied into the state array. If the input block is represented as in0, in1, in2, ..., in15, then the state array is populated as follows:

$$\text{State} = \begin{bmatrix} \text{in}{0} & \text{in}{4} & \text{in}{8} & \text{in}{12} \\ \text{in}{1} & \text{in}{5} & \text{in}{9} & \text{in}{13} \\ \text{in}{2} & \text{in}{6} & \text{in}{10} & \text{in}{14} \\ \text{in}{3} & \text{in}{7} & \text{in}{11} & \text{in}{15} \end{bmatrix}$$

Then the four transformations (SubBytes, ShiftRows, MixColumns, and AddRoundKey) operate on this state array, modifying its contents in each round. (Which will be discussed in the paper later)

Now, we need to understand the 2 key pillars of the Advanced Encryption Standard.

Confusion and Diffusion: The Cornerstones of Secure Encryption

Introduction

Claude Shannon, a pioneer in information theory and cryptography, introduced the concepts of confusion and diffusion in his seminal 1949 paper, "Communication Theory of Secrecy Systems." These two principles are the foundation of modern symmetric-key cryptography, including AES. They ensure that the relationship between the plaintext, key, and ciphertext is as complex and obscured as possible, making it extremely difficult for an attacker to break the encryption.

Confusion

Confusion aims to make the relationship between the encryption key and the ciphertext as complex and unintelligible as possible. In other words, each bit of the ciphertext should depend on several parts of the key in a complicated way.

In AES, the SubBytes transformation is the primary source of confusion in AES. The S-box (substitution box) used in SubBytes is a non-linear function that takes a byte as input and outputs another byte based on a pre-defined table. This table is designed to obscure the relationship between the input and output bytes, making it difficult to derive the key from the ciphertext.

If the relationship between the key and ciphertext is too simple, an attacker can analyze the ciphertext and deduce information about the key, potentially leading to a complete break of the encryption. Confusion makes this type of analysis much harder.

Diffusion

On the other hand, Diffusion aims to spread the statistical properties of the plaintext over the entire ciphertext. In other words, if you change a single bit of the plaintext, ideally, about half of the bits in the ciphertext should change, and in an unpredictable way. Similarly, each bit of the ciphertext should depend on many bits of the plaintext.

Diffusion is typically achieved through permutation or mixing operations. These operations rearrange the bits or bytes of the data, spreading the influence of each input bit across multiple output bits.

The ShiftRows transformation provides diffusion by shifting the rows of the state array. This ensures that bits from one part of the block are moved to other parts, spreading their influence.
The MixColumns transformation provides further diffusion by mixing the bytes within each column of the state array. This ensures that each byte in a column affects all the other bytes in the same column during the transformation.

If there is little or no diffusion, patterns in the plaintext may be visible in the ciphertext. This could allow an attacker to gain information about the plaintext, potentially leading to a partial or complete recovery of the original message. Diffusion makes it much harder for an attacker to exploit patterns in the plaintext

Analogy

Think of confusion as hiding the ingredients of a cake and diffusion as mixing them thoroughly. If the ingredients are not hidden (no confusion), anyone can easily figure out the recipe. If the ingredients are hidden but not mixed well (confusion but no diffusion), you might be able to identify clumps of individual ingredients, giving you clues about the recipe. But if the ingredients are both hidden and thoroughly mixed, it becomes very difficult to determine the original recipe.

The Five Key Operations of AES

The Round Key Conundrum: A Naive Approach

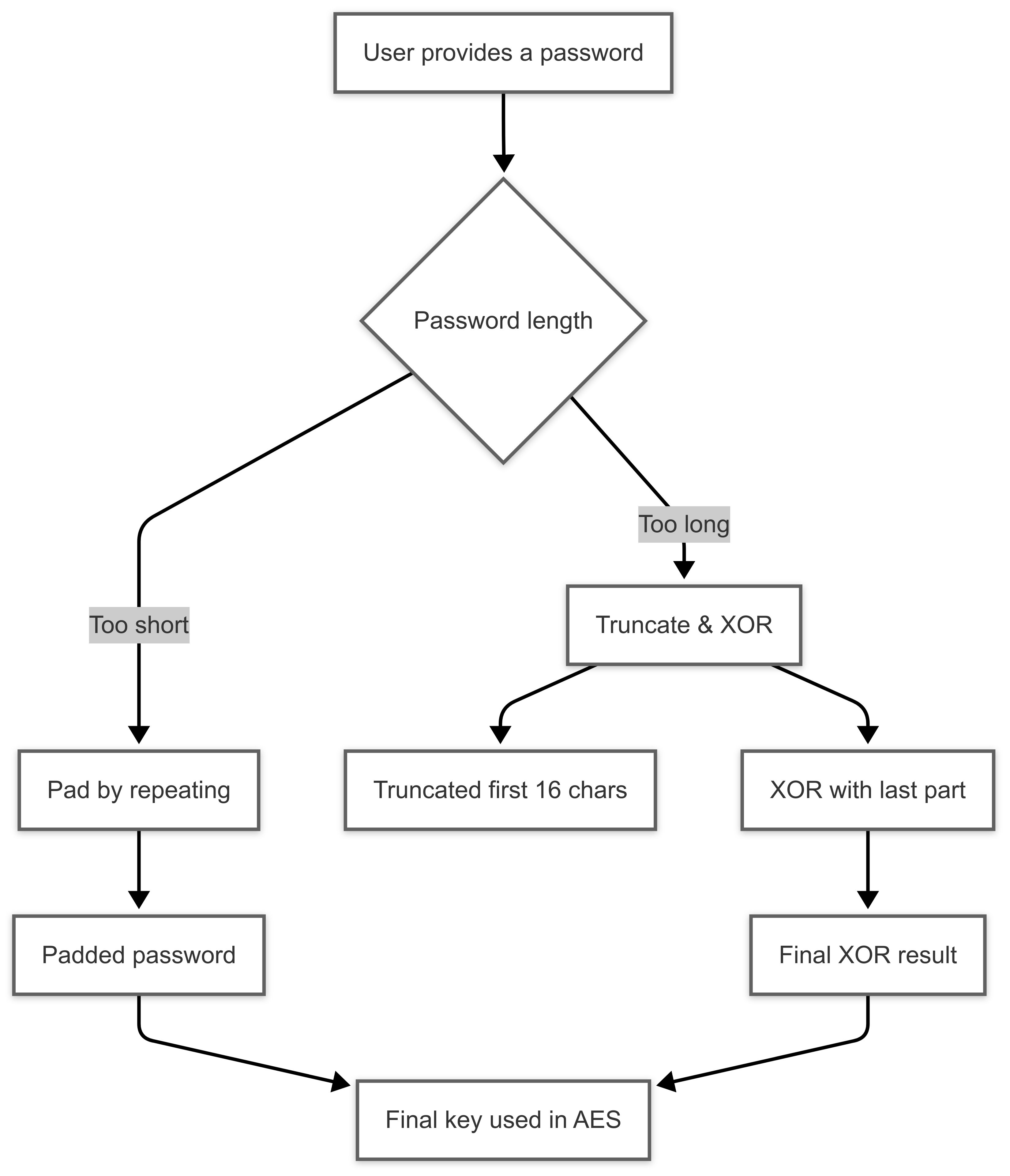
Before diving into the individual operations, let's address how we handle the initial key that the user provides. AES operates with fixed key sizes (128, 192, or 256 bits). To ensure compatibility, we need to adapt the user's input to fit these requirements.

Handling User-Provided Passwords:

If a user provides a password (which is likely to be of variable length), we must convert it into a key of the appropriate size. Here’s how we can handle this:

Padding (if too short): If the password is shorter than the required key length (e.g., 16 characters for a 128-bit key), we need to pad it. A simple approach is to repeat the password until it reaches the required length.
- Example:
  - User password: rishi@2220 (9 characters)
  - Required length: 16 characters (128 bits)
  - Padded password: rishi@2220rishi@
Truncation & XOR (if too long): If the password is longer than the required key length, we can truncate it, but it's more secure to combine the extra characters with the beginning through XOR operations. Here’s how that might work in principle:

Example

User password: ThisIsAVeryLongPassword (23 Characters)
Required Length: 16 Characters (128 bits)
We take the first 16 characters: ThisIsAVeryLong
XOR them with the last 7 (padded to 16)

$$\begin{array}{c} \texttt{ThisIsAVeryLong} \\ \texttt{Password000000} \\ \hline \textbf{XOR} \\ \hline \texttt{Result} \end{array}$$

Key Expansion in AES

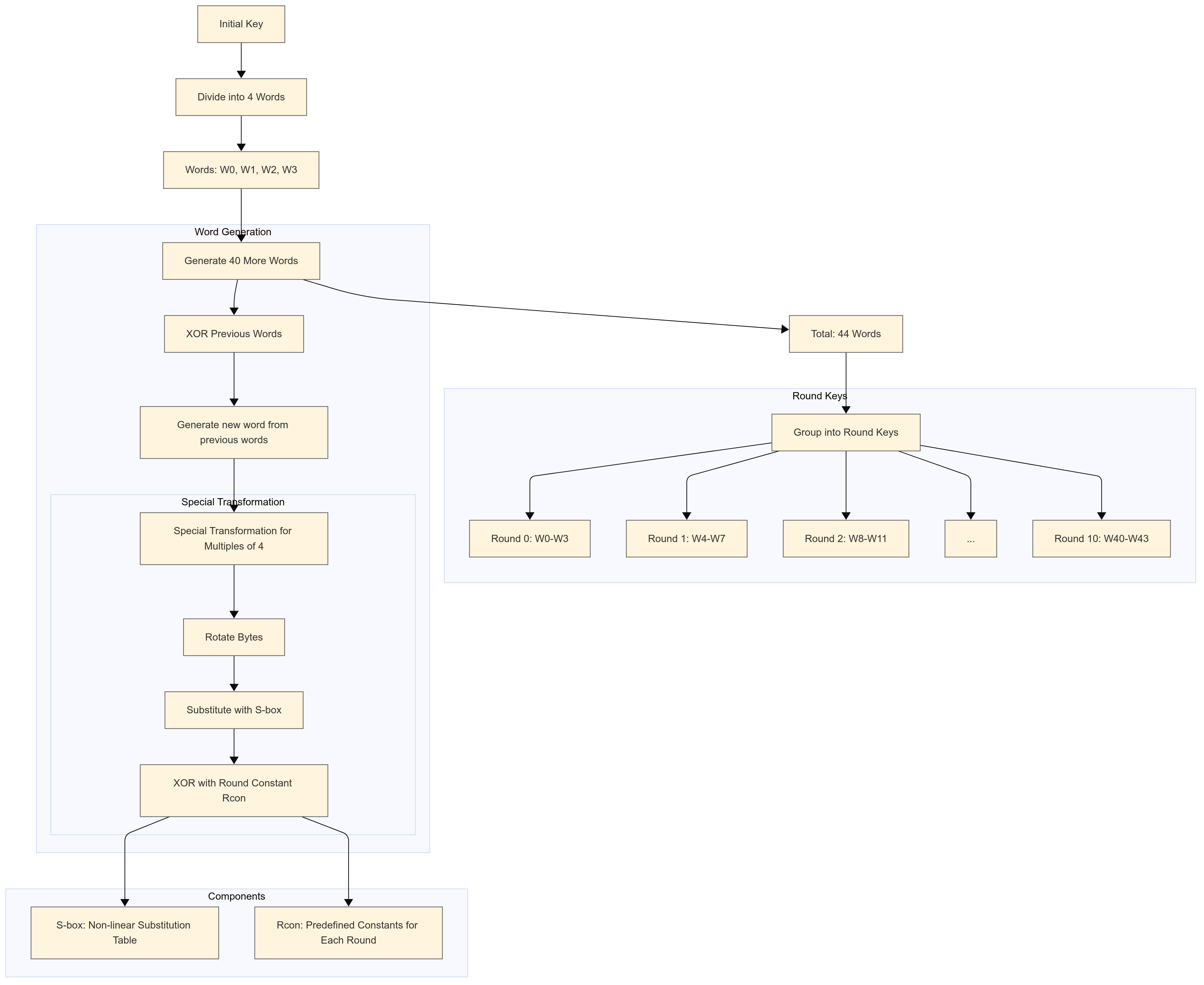
Once we have an initial key of the correct size, we must generate multiple round keys. AES requires a different key for each round of encryption to ensure that the same key is not used repeatedly, which would be insecure, as discussed earlier.

In AES 128, we need 11 round keys (one initial key + 10 round keys), which will make the original 16-byte key to a large 176-byte (11 × 16) one.

How the expansion works

We need to convert and divide the original key into chunks of 4 of 4 bytes each, called words (in cryptography).

$$\text{Original key: } [W_0][W_1][W_2][W_3]$$

To create the expanded key, we generate 40 more words, so we end up with 44 total:

$$\text{Expanded Key: } [W0][W1][W2][W3][W4][W5]...[W43]$$

Each group of 4 words makes up one round key:

Words 0-3: Initial round key
Words 4-7: Round 1 key
Words 8-11: Round 2 key
And so on...

Final Expansion Algorithm

Each new word is created by XORing two previous words.

$$W[i] = W[i-4] \oplus W[i-1]$$

For words at positions that are multiples of 4 (W4, W8, W12, etc.), we apply extra transformations.

$$W[i] = W[i-4] \oplus st(W[i-1])$$

Special transformation

Rotate: Shift the bytes in the word to the left by one position.

$$[a,b,c,d] → [b,c,d,a]$$

Substitute: Replace each byte with its corresponding value from the S-box (the same S-box used in the SubBytes transformation).

$$[b,c,d] → [S(b),S(c),S(d)]$$

XOR with round constant: XOR the first byte with a predefined round constant.

$$[S(b),S(c),S(d)] → [S(b) \oplus {rcon}[round],S(c),S(d)]$$

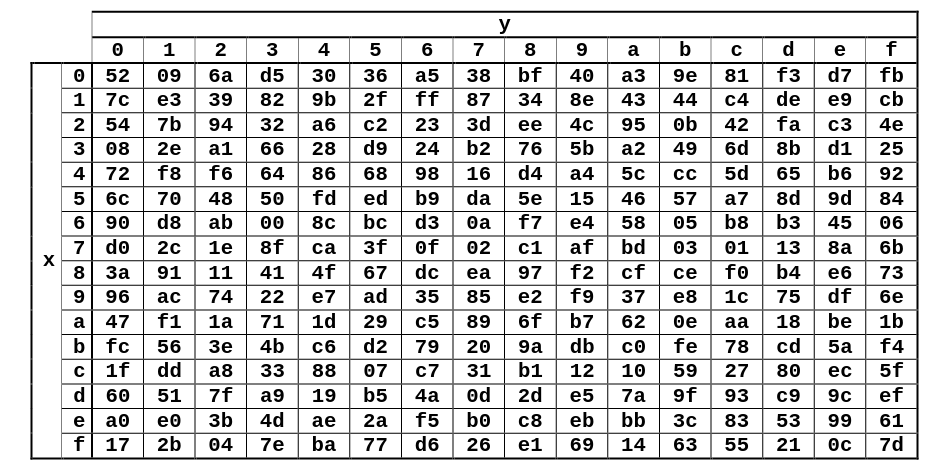
The S-box and Round Constants
- S-box (Substitution Box): A fixed 16×16 lookup table (256 entries). Each byte value 0-255 maps to a different byte value. Designed to introduce non-linearity into the encryption. The substitution is not a simple mathematical formula but a carefully designed mapping.
- Round Constants (Rcon): A series of predefined values used in the key expansion. Only the first byte of each round constant is non-zero. Values: 01, 02, 04, 08, 10, 20, 40, 80, 1B, 36... Notice that these values double each time (in the finite field). Ensures each round key is different and depends on the round number.

SubBytes: Introducing Confusion, One Byte at a Time

With the round keys generated, let’s now examine the SubBytes transformation, a crucial step in providing confusion.

The SubBytes transformation operates independently on each byte of the state. Each byte is replaced with another byte according to a lookup table called the S-box (Substitution box).

The S-box is a 256-byte table that provides a non-linear mapping from input bytes to output bytes. It is designed to be invertible, meaning that for each output byte, there is a unique input byte that maps to it. This is necessary for decryption.

It's important to note that while we describe the SubBytes operation as applying to each byte individually, in practice, these operations are performed simultaneously across all 16 bytes of the state. This is a key aspect of AES's efficiency.

$$\text{Initial State:} \quad \begin{bmatrix} a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} \\ a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix}$$

$$ \text{After SubBytes:} \quad \begin{bmatrix} S(a{0,0}) & S(a{0,1}) & S(a{0,2}) & S(a{0,3}) \ S(a{1,0}) & S(a{1,1}) & S(a{1,2}) & S(a{1,3}) \ S(a{2,0}) & S(a{2,1}) & S(a{2,2}) & S(a{2,3}) \ S(a{3,0}) & S(a{3,1}) & S(a{3,2}) & S(a{3,3}) \end{bmatrix}$$

Importance of SubBytes:

Non-Linearity: The S-box introduces non-linearity into the algorithm, which is essential for preventing linear cryptanalysis attacks.
Confusion: The S-box provides confusion by obscuring the relationship between the input and output bytes. Small changes in the input byte result in unpredictable changes in the output byte.
Avalanche Effect: The S-box contributes to the avalanche effect, where a small change in the input data leads to a large and unpredictable change in the output data.

ShiftRows: Creating Horizontal Diffusion

The ShiftRows transformation operates on the State, which is a 4x4 array of bytes. The transformation proceeds as follows:

Row 0: No shift is performed. The first row of the state remains unchanged.
Row 1: A cyclic left shift of one byte is performed. This means the first byte moves to the last position, and all other bytes shift one position to the left.
Row 2: A cyclic left shift of two bytes is performed. The first two bytes move to the end, and the remaining bytes shift two positions to the left.
Row 3: A cyclic left shift of three bytes is performed. The first three bytes move to the end, and the remaining byte shifts three positions to the left.

Visualizing ShiftRows:

Let's consider a 4x4 state array:

After the ShiftRows transformation, the state becomes:

$$\text{After ShiftRows:} \quad \begin{bmatrix} a_{0,0} & a_{0,1} & a_{0,2} & a_{0,3} \\ % Row 0 - No Shift a_{1,1} & a_{1,2} & a_{1,3} & a_{1,0} \\ % Row 1 - Shift 1 byte to the left a_{2,2} & a_{2,3} & a_{2,0} & a_{2,1} \\ % Row 2 - Shift 2 bytes to the left a_{3,3} & a_{3,0} & a_{3,1} & a_{3,2} % Row 3 - Shift 3 bytes to the left \end{bmatrix}$$

Why ShiftRows is Important:

This seemingly simple operation ensures that bytes that were in the same column are now dispersed across different columns, creating horizontal diffusion.

Let's break down why this "horizontal diffusion" is important:

Breaking Column Dependency: After SubBytes, each byte in a column is related to the key through the AddRoundKey operation and the S-box substitution. ShiftRows breaks this column dependency.
Spreading Byte Influence: ShiftRows spreads the influence of each byte across the state. If a single byte is changed, after ShiftRows, its influence will be felt in different columns in the next round.
Preparation for MixColumns: ShiftRows sets up the state for the MixColumns transformation, which provides further diffusion and mixing within the columns.

MixColumns: Achieving Vertical Diffusion with Galois Field Arithmetic

Following ShiftRows, the MixColumns transformation provides further diffusion by mixing the bytes within each column of the state. This is where we leverage Galois Field arithmetic to achieve strong diffusion properties.

MixColumns is designed to mix the values within each column of the state matrix, ensuring that each byte in the output column depends on all bytes in the input column. This provides diffusion by spreading the influence of each input byte across multiple output bytes.

Together, ShiftRows and MixColumns ensure that changing even one bit of the plaintext will eventually affect all bytes in the state—achieving the diffusion property Shannon described.

Mathematical Framework: Finite Field Arithmetic GF(2^8):

Before understanding the operation itself, it's important to understand the mathematical framework:

A finite field (or Galois Field) is a mathematical structure with a finite number of elements where the operations of addition, subtraction, multiplication, and division (except by 0) are defined and follow certain axioms.

In AES, we use the finite field GF(2^8), which:

Contains exactly 2^8 = 256 elements (all possible byte values)
Has operations defined that always result in another element within the field

Polynomial Representation:

In GF(2^8), each byte is represented as a polynomial with binary coefficients:

For example, the byte 0x57 (01010111 in binary) represents:

$$0×2^7 + 1×2^6 + 0×2^5 + 1×2^4 + 0×2^3 + 1×2^2 + 1×2^1 + 1×2^0$$

Or more simply:

$$x^6 + x^4 + x^2 + x + 1$$

Each bit in the binary representation tells us if that power of x is present in the polynomial. Operations in the Finite Field:

Addition and subtraction are both performed using XOR (⊕) operations on the corresponding bits:

$$0x57 \oplus 0x83 = 01010111 \oplus 10000011 = 11010100 = 0xD4$$

In polynomial terms:

$$(x^6 + x^4 + x^2 + x + 1) + (x^7 + x + 1) = x^7 + x^6 + x^4 + x^2 = 0xD4$$

Multiplication is more complex. When we multiply two polynomials in the usual way, we might get terms with degrees higher than 7, which would no longer fit in a byte.

When multiplying polynomials, we need a way to "reduce" the result to ensure it stays within our field. This is where the reduction polynomial (also called the irreducible polynomial) comes in.

For AES, the reduction polynomial is:

$$p(x) = x^8 + x^4 + x^3 + x + 1$$

In hexadecimal, this is represented as 0x11B (100011011 in binary).

An irreducible polynomial cannot be factored into smaller non-constant polynomials over the same field. It's conceptually similar to prime numbers in integer arithmetic.

In GF(2), the field with just two elements (0 and 1), a polynomial is irreducible if it cannot be written as a product of two or more non-constant polynomials with coefficients in GF(2).

The polynomial x^8 + x^4 + x^3 + x + 1 is irreducible over GF(2), which makes it suitable for constructing GF(2^8).

An irreducible polynomial cannot be factored into smaller non-constant polynomials over the same field. It's conceptually similar to prime numbers in integer arithmetic.

In GF(2), the field with just two elements (0 and 1), a polynomial is irreducible if it cannot be written as a product of two or more non-constant polynomials with coefficients in GF(2).

The polynomial x^8 + x^4 + x^3 + x + 1 is irreducible over GF(2), which makes it suitable for constructing GF(2^8).

This is analogous to how we might compute 17 mod 5:

Divide 17 by 5: 17 = 3×5 + 2
The remainder, 2, is our answer

For polynomials, we perform polynomial long division and take the remainder.

Example:

Let's multiply 0xAC by x (or 2) in GF(2^8):

0xAC = 10101100 in binary, representing the polynomial:

$$x^7 + x^5 + x^3 + x^2$$

Multiply by x (shift left):

In binary: 101011000 (note this is 9 bits)

$$x(x^7 + x^5 + x^3 + x^2) = x^8 + x^6 + x^4 + x^3$$

Since we have an x^8 term, we need to reduce:

$$x^8 |p(x)| = x^4 + x^3 + x + 1$$

So our result becomes:

$$(x^6 + x^4 + x^3) + (x^4 + x^3 + x + 1) = x^6 + x + 1$$
In binary: 01000011 = 0x43

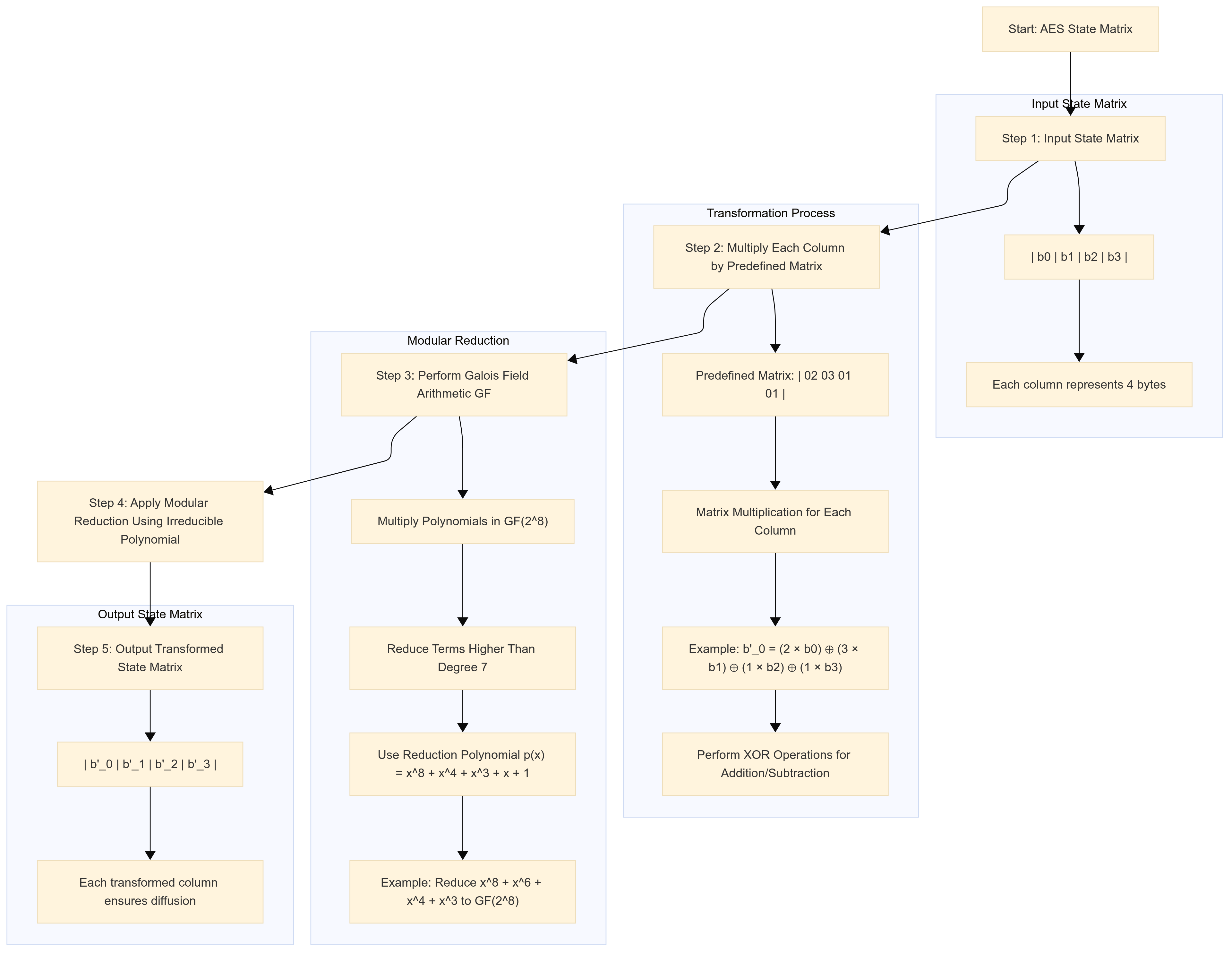
In MixColums we multiply with a specific matrix. The matrix multiplication is represented as:

$$\begin{bmatrix} b'_0 \\ b'_1 \\ b'_2 \\ b'_3 \end{bmatrix} = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \end{bmatrix} \begin{bmatrix} b_0 \\ b_1 \\ b_2 \\ b_3 \end{bmatrix}$$

This matrix is carefully chosen to ensure that each byte in the output column depends on all four bytes in the input column in a complex way. The specific arrangement of the coefficients {01}, {02}, and {03} ensures that no byte is left unaffected and that the influence of each input byte is spread throughout the output.

The MixColumns transformation is designed to be a Maximum Distance Separable (MDS) code. MDS codes provide the best possible diffusion for a given block size and symbol size.

In simpler terms, an MDS code maximizes the number of changed output bytes for a given number of changed input bytes. This means that even a small change in the input will result in a large change in the output, which is exactly what we want for strong diffusion.

For decryption, we need to be able to reverse the MixColumns transformation. This means the matrix must be invertible. The chosen matrix has an inverse that can be efficiently implemented using Galois Field arithmetic. This is crucial for ensuring that decryption is possible and efficient. The inverse matrix is:

Expanding this matrix multiplication, we get:

$$\begin{align*} b'_0 & = (2 \times b_0) \oplus (3 \times b_1) \oplus (1 \times b_2) \oplus (1 \times b_3) \\ b'_1 & = (1 \times b_0) \oplus (2 \times b_1) \oplus (3 \times b_2) \oplus (1 \times b_3) \\ b'_2 & = (1 \times b_0) \oplus (1 \times b_1) \oplus (2 \times b_2) \oplus (3 \times b_3) \\ b'_3 & = (3 \times b_0) \oplus (1 \times b_1) \oplus (1 \times b_2) \oplus (2 \times b_3) \end{align*}$$

Now we can understand the multiplication by 1, 2, 3 in GF(2^8).

Multiplication by 01 is just the identity operation (no change).
Multiplication by 02 was discussed earlier, but here is the gist:

It is implemented as a 1-bit left shift. However, since we're working in a finite field, we need to perform a modular reduction if the most significant bit (MSB) of the original byte was set. This reduction is achieved by XORing with the polynomial x^8 + x^4 + x^3 + x + 1. Since we've already shifted (implying the x^8 term), we only need to XOR with x^4 + x^3 + x + 1, which is represented as 0x1B.

Multiplication by 3 can be achieved by combining multiplication by 2 and XORing with the original value. This is because 3 is equivalent to (2 + 1), and in GF(2^8), addition is XOR.

$$3 \times b = (2 \times b) \oplus b$$

These operations are relatively simple and can be performed quickly, making AES efficient.

MixColumns provides vertical diffusion, ensuring each byte in a column affects all bytes in that column. Combined with ShiftRows, it provides complete diffusion, ensuring changes quickly propagate throughout the state. The combination of shifting and mixing after a few rounds results in each output bit depending on every input bit

4. AddRoundKey: Combining with the Key

In this final step of each round, the state is combined with a round key derived from the main encryption key. This is done using the XOR operation we discussed earlier.

While using a single key with XOR isn't secure enough by itself, when combined with the other operations and applied across multiple rounds with different derived keys, it creates a robust encryption mechanism.

The Complete AES Algorithm: Putting It All Together

Now that we've examined each of the individual transformations, let's see how they fit together in the complete AES algorithm.

Key Expansion:
- The original key is expanded into multiple round keys using the key schedule algorithm.
- The number of round keys needed depends on the key size (128, 192, or 256 bits) and the number of rounds.
Initial Round:
- The plaintext (input data) is copied into the State array.
- An initial round key is XORed with the State using the AddRoundKey transformation.
Main Rounds:
- A series of rounds is performed, each consisting of four transformations:
  - SubBytes: Byte substitution using the S-box.
  - ShiftRows: Cyclically shift the rows of the State.
  - MixColumns: Mix the bytes within each column of the State.
  - AddRoundKey: XOR the State with the round key for that round.
Final Round:
- The final round is similar to the main rounds, but it omits the MixColumns transformation. This is done for mathematical reasons related to the invertibility of the algorithm.
  - SubBytes: Byte substitution using the S-box.
  - ShiftRows: Cyclically shift the rows of the State.
  - AddRoundKey: XOR the State with the final round key.

Number of Rounds:

The number of rounds (Nr) depends on the key size (Nk).

AES-128: 10 rounds (Nk = 4, Nr = 10)
AES-192: 12 rounds (Nk = 6, Nr = 12)
AES-256: 14 rounds (Nk = 8, Nr = 14)

Here is graph describing the whole process.

Beyond the Algorithm: Introducing Cipher Block Chaining (CBC) Mode

Now that we've covered the core AES algorithm, it's crucial to understand how it's used in practice. AES is a block cipher, which means it encrypts data in fixed-size blocks (128 bits in the case of AES). However, most real-world data isn't conveniently sized into 128-bit blocks. Also, encrypting the same plaintext block with the same key will always produce the same ciphertext block, which can reveal patterns to an attacker. That is, Electronic Codebook (ECB) mode is insecure.

That's where modes of operation come in. These modes describe how to repeatedly apply a block cipher's single-block operation to securely transform larger amounts of data than the block size. One of the most common and important modes is Cipher Block Chaining (CBC).

What is Cipher Block Chaining (CBC)?

CBC is a block cipher mode of operation that enhances security by making each ciphertext block dependent on all preceding plaintext blocks. This is achieved by XORing each plaintext block with the previous ciphertext block before encryption.

How CBC Works:

Initialization Vector (IV): The first plaintext block is XORed with a random value called the Initialization Vector (IV). The IV is the same size as the block size (128 bits for AES). The IV is not secret, but it must be unpredictable.
Encryption: The result of the XOR operation is then encrypted using the block cipher (AES in our case) with the secret key. This produces the first ciphertext block.
Chaining: For each subsequent plaintext block, the process is as follows:
- XOR the current plaintext block with the previous ciphertext block.
- Encrypt the result using the block cipher with the secret key. This produces the current ciphertext block.
Decryption: The decryption process reverses the steps:
- Decrypt the ciphertext block using the block cipher with the secret key.
- XOR the result with the previous ciphertext block (or the IV for the first block) to recover the plaintext block.

AES in the Real World

Today, AES is the gold standard for symmetric encryption. Its widespread adoption is due to several factors:

Security: Despite intensive cryptanalysis, no practical attacks exist against properly implemented AES.
Performance: AES is fast, especially with hardware acceleration built into modern processors.
Flexibility: With different key sizes, AES can be adapted to various security requirements.

You'll find AES protecting:

HTTPS connections when you visit secure websites
VPN tunnels encrypting your internet traffic
Full-disk encryption on your devices
Secure messaging apps like Signal and WhatsApp
Wi-Fi networks using WPA2/WPA3 security

Putting It Into Practice: Introducing Axon

To help you further explore and experiment with the concepts discussed in this paper/blog, I've created a command-line tool called Axon. Axon provides a practical way to perform AES encryption and decryption using different modes of operation, including CBC.

Downloading and Installing Axon:

Axon is available on GitHub at github.com/RishiAhuja/axon.

Conclusion: Further Exploration

In this blog post, we've journeyed through the intricacies of the Advanced Encryption Standard (AES), a cornerstone of modern cryptography. We started with a naive approach to key scheduling, then explored its five key operations: SubBytes, ShiftRows, MixColumns, and AddRoundKey. Finally, we saw how AES is deployed through Cipher Block Chaining (CBC), to be resistant to the shortcomings of ECB mode. With Axon, you are able to try all those modes in real time and witness the results.

By understanding these fundamental principles, you're equipped to appreciate the complexities and strengths of AES and its role in securing digital information.

Where to Go From Here:

Experiment with Axon: Download and use the Axon command-line tool to gain hands-on experience with AES encryption and decryption.
Explore Other Modes of Operation: CBC is just one of many modes of operation. Research other modes like CTR, GCM, and CFB to understand their strengths and weaknesses.
Dive Deeper into Galois Field Arithmetic: Understanding the mathematics behind GF(2^8) will provide a deeper appreciation for the inner workings of AES.

I drew much of this information from the official NIST document (https://doi.org/10.6028/NIST.FIPS.197-upd1), which you can access for even greater detail.

And that's it! Thank you for taking the time to read through this exploration of AES. I hope you found these insights valuable. Understanding these fundamental concepts is crucial for anyone interested in cybersecurity and data protection.

If you found this guide helpful, I'd love to connect:

Happy coding!

Bits of Trust: The Elegance of AES

Table of contents