Jane Street puzzle writeup: Hall of Mirrors 3

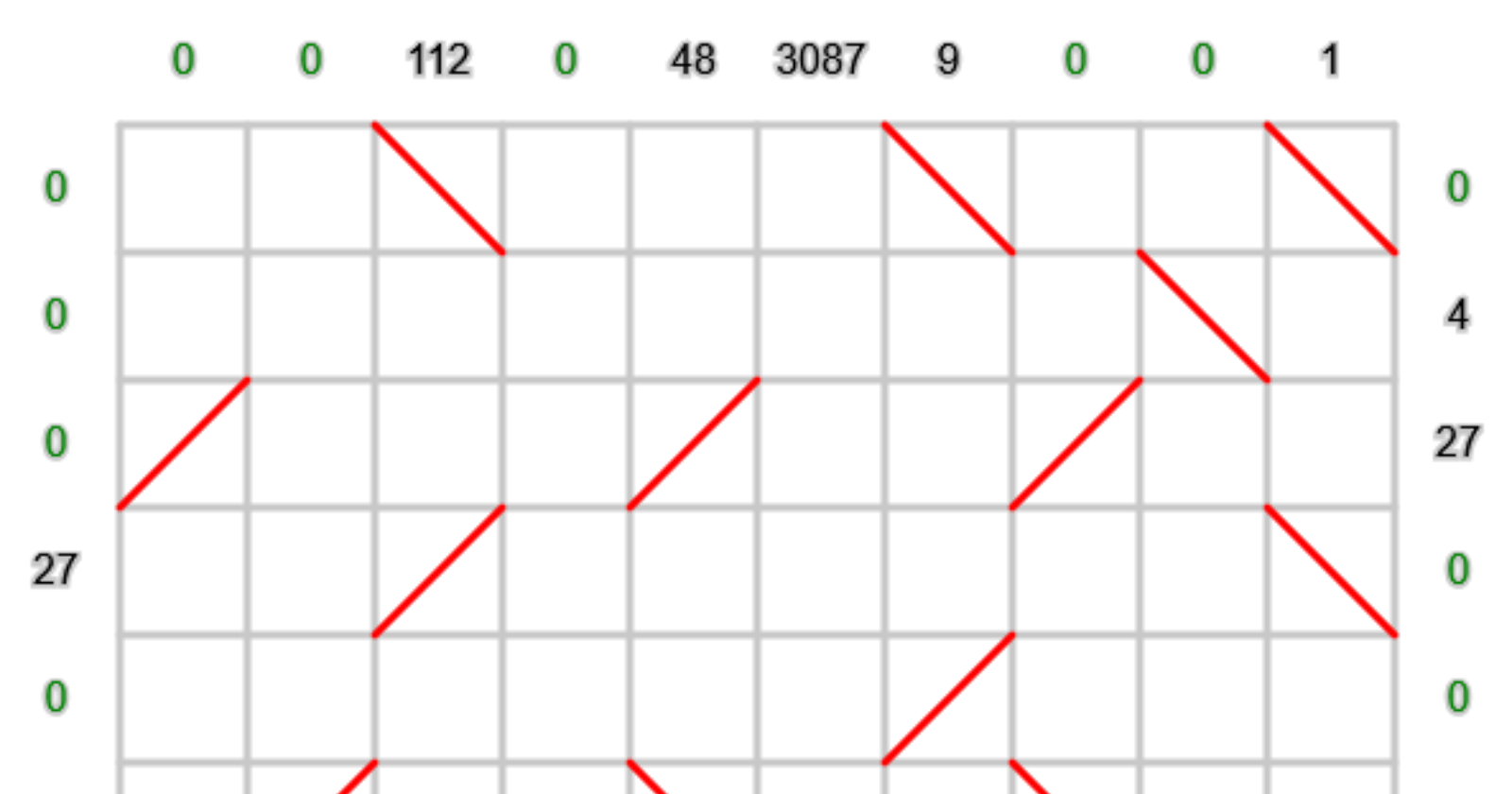
After solving the last puzzle just in the nick in time, I was eager to dive into the next one. Fortunately, this one turned out to be much more straightforward.

I started by building a visualizer, to better understand how the puzzle functioned. After playing around I realized the puzzle could most likely be solved by hand, so I enhanced the tool with features like automatic length counting to streamline the process.

I started by solving the small numbers in the top right corner and the 5 at the bottom, as they had only one valid configuration. Since 5 is a prime number and 1 forces the mirror to be in the top right corner, this limits where the mirror for the number 4 can go, as mirrors can't be placed in orthogonally adjacent cells. From there, I focused on the larger numbers, using prime factorization to figure out the needed segment lengths.

For example, 3087 = 3 × 3 × 7 × 7 × 7, meaning I needed either two 3-segments (or one 9-segment) and three 7-segments.

I worked on fitting the segments into the grid while resolving any conflicts. Additionally I tried to use as few mirrors as possible

Two hours of experimenting later, I found the solution and submitted it within the first 24 hours of the puzzle’s release.

I've attached the visualizer with the solution below.

• ENTER = Show Solution

• Click on a number = Enable/Disable Laser

• Click on a space = Cycle through mirror options