Mastering Two Pointers: Solve Array Problems Faster

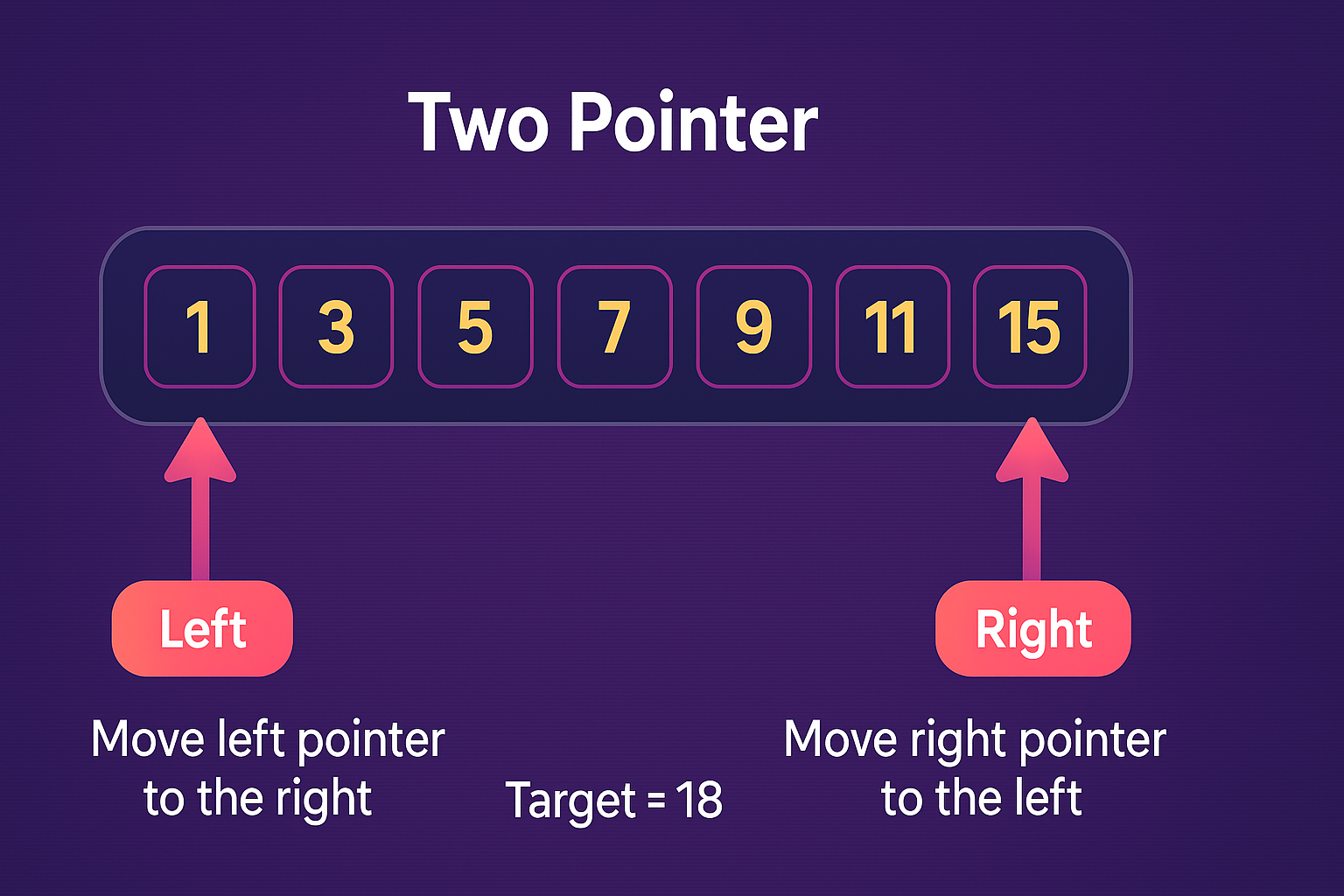
An Introduction to the Two Pointer Technique: The Two Pointer technique is a fundamental algorithmic approach used in solving array and string problems efficiently. It involves maintaining two indices (pointers) that traverse the array from different directions or in a specific manner to solve problems in O(N) time complexity instead of O(N²) for brute force solutions.

Why Do we use the Two Pointer Technique?

• Optimized Performance: It reduces O(N²) complexity (brute force) to O(N) or O(N Log N) in many Cases.

• Efficient for Sorted Arrays: Many Problems involving sorted arrays or lists can be solved efficiently with two pointers.

• Reduces Space Complexity: In most cases, It requires O(1) extra space.

• Simple to Implement: It makes complex problems easier to understand and solve.

Types Of Two Pointer Approaches

1. Opposite Direction (Two Ends)

   Used When -

   → The array is Sorted.

   → We need to find pairs that satisfy the conditions (e.g., sum of two numbers).

   → We need to check for symmetry (e.g. palindrome checking).
   🔠 Example: Two Sum in a Sorted Array.

   Problem: Given a sorted array, find two numbers that add up to a target sum.

   Visualization:

   Array: [1, 3, 5, 7, 10, 15] Target = 12

   | Left Pointer (L) | Right Pointer (R) | Sum (arr[L] + arr[R]) | Action | | --- | --- | --- | --- | | 1 (index 0) | 15 (index 5) | 1 + 15 = 16 | Sum > Target → Move R left | | 1 (index 0) | 10 (index 4) | 1 + 10 = 11 | Sum < Target → Move L right | | 3 (index 1) | 10 (index 4) | 3 + 10 = 13 | Sum > Target → Move R left | | 3 (index 1) | 7 (index 3) | 3 + 7 = 10 | Sum < Target → Move L right | | 5 (index 2) | 7 (index 3) | 5 + 7 = 12 | Pair Found → (5, 7) ✅ |

   Result:

   Pair (5,7) forms the target sum 12.

   JavaScript:

    function twoSumOpposite(arr, target) {
        let left = 0,
            right = arr.length - 1;
   
        while (left < right) {
            sum = arr[left] + arr[right];
            if (sum === target) {
                return [arr[left], arr[right]];
            } else if (sum < target) {
                left++;
            } else {
                right--;
            }
        }
        return [];
    }
   
    let arr = [1, 2, 3, 4, 6],
        target = 9;
    console.log(twoSumOpposite(arr, target));
   

   ✅ Time Complexity: O(N)

2. Same Direction (Sliding Window)

   Used When -

   → Finding Subarrays with a condition.

   → Finding Longest/Shortest Substrings with unique properties.

   →When dealing with strings or continuous arrays.

   📌 Example : Longest Substring Without Repeating Characters

   Problem: Find the length of the longest substring without repeating characters.

   Example: "abcabcbb"

   ✅ Output: 3 ("abc")

   Index (end)

   | | Char | start | charIndex (last seen index) | Substring | Length (maxLength) | | --- | --- | --- | --- | --- | --- | | 0 | a | 0 | {a: 0} | "a" | 1 | | 1 | b | 0 | {a: 0, b: 1} | "ab" | 2 | | 2 | c | 0 | {a: 0, b: 1, c: 2} | "abc" | 3 | | 3 | a | 1 | {a: 3, b: 1, c: 2} | "bca" | 3 | | 4 | b | 2 | {a: 3, b: 4, c: 2} | "cab" | 3 | | 5 | c | 3 | {a: 3, b: 4, c: 5} | "abc" | 3 | | 6 | b | 5 | {a: 3, b: 6, c: 5} | "cb" | 3 | | 7 | b | 7 | {a: 3, b: 7, c: 5} | "b" | 3 |

   JavaScript

   1.   let s = 'abcabcbb';
        let charSet = new Set();
        let left = 0, maxLength = 0;
      
        for (let right = 0; right < s.length; right++) {
            while (charSet.has(s[right])) {
                charSet.delete(s[left]);
                left++;
            }
            charSet.add(s[right]);
            maxLength = Math.max(maxLength, right - left + 1);
        }
        console.log(maxLength);
      

      ✅ Time Complexity: O(N)

3. Two Pointers on Different Arrays

   → Merging two sorted arrays.

   → Finding intersections between two sorted arrays.

   Example 3: Merge Two Sorted Arrays

   Problem: Given two sorted arrays, merge them into one sorted array.

   🔢 Example:
   arr1 = [1, 3, 5], arr2 = [2, 4, 6]
   ✅ Output: [1, 2, 3, 4, 5, 6]

   | Step | i | j | arr1[i] | arr2[j] | Result | | --- | --- | --- | --- | --- | --- | | 1 | 0 | 0 | 1 | 2 | [1] | | 2 | 1 | 0 | 3 | 2 | [1, 2] | | 3 | 1 | 1 | 3 | 4 | [1, 2, 3] | | 4 | 2 | 1 | 5 | 4 | [1, 2, 3, 4] | | 5 | 2 | 2 | 5 | 6 | [1, 2, 3, 4, 5] | | 6 | 3 | 2 | X | 6 | [1, 2, 3, 4, 5, 6] |

   ✅ Final Merged Array: [1, 2, 3, 4, 5, 6]

   JavaScript

    function mergeTwoDifferentArrays(arr1, arr2) {
        let i = 0, j = 0;
        let mergeArray = [];
        while (i < arr1.length && j < arr2.length) {
            if (arr1[i] < arr2[j]) {
                mergeArray.push(arr1[i]);
                i++;
            } else {
                mergeArray.push(arr2[j]);
                j++
            }
        }
        while (i < arr1.length) {
            mergeArray.push(arr1[i]);
            i++;
        }
        while (j < arr2.length) {
            mergeArray.push(arr2[j]);
            j++
        }
        return mergeArray;
    }
   
    console.log(mergeTwoDifferentArrays([1, 3, 5], [2, 4, 6]))
   

   ✅ Time Complexity: O(n + m)

🚀 Conclusion: Two Pointer Technique Summary

The Two Pointer technique is a powerful optimization strategy that reduces time complexity from O(N²) to O(N) in many cases. It is widely used in arrays, strings, and linked lists for solving problems efficiently.