If you can answer the following question, you already have some notion of this scheme:

How can I share a story with my close friends such that not one person can paint the whole picture?

I came across this when I was setting up a Vault server. One of the features of Vault is to “seal” and “unseal” the encryption key that protects your secrets. Check out Vault’s documentation to know more.

Background

Adi Shamir, widely known as co-creator of the Rivest-Shamir-Adleman (RSA) algorithm and the Feige-Fiat-Shamir (FFS) identification scheme, published a paper on how to share a secret in 1979. It is one of the most cited papers in cryptography as it demonstrated an elegant solution to disseminate confidential information in a secure manner. Key concepts such as polynomial interpolation for secret sharing and the notion of information-theoretic security, introduced in this paper, became fundamental to modern cryptography.

How It Works

Choose the minimum number of shares k and total number of shares n needed.
Create a random polynomial of degree k-1 where the secret is the constant term.
Generate n points on this polynomial to create the shares.
Distribute these shares among participants in a secure manner.

For example

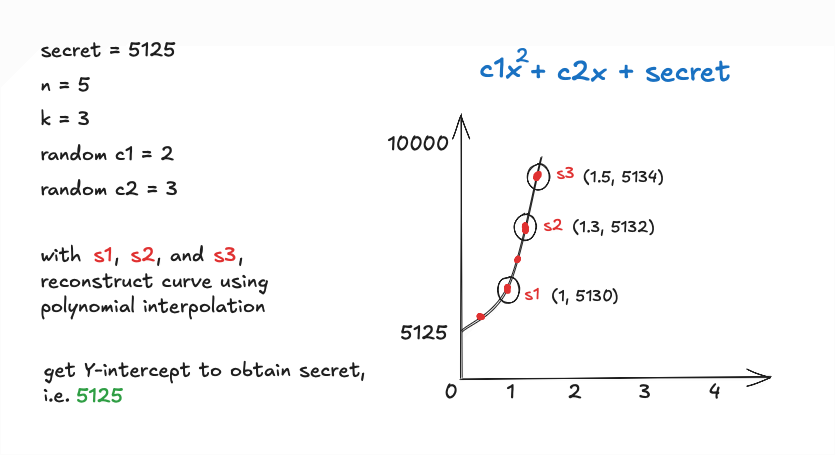
Let’s assume we want to share a secret number - 5125 - among 5 people. We would like to have at least 3 people’s shares to reconstruct the number. So, we have: secret = 5125, n = 5, k = 3.

In this case, since we need at least 3 shares to get the secret, we need a 2nd degree polynomial. Let’s use a simple set of coefficients - 2 and 3 - for this example but remember, actual implementations will choose random coefficients.

Computing the shares and distributing them are quite straightforward once we have the coefficients for the polynomial. The novelty here is in retrieving the secret using some of these shares. This requires a numerical analysis technique called Polynomial Interpolation. By applying this technique, the curve on which these shares exist can be computed. Once we have the curve, the secret is the Y-intercept of the curve, as illustrated below.

Key Properties

Perfect secrecy: k-1 shares reveal nothing about the secret.
Threshold scheme: Exactly k shares are needed to reconstruct the secret.
Information-theoretic security: Also known as unconditional security, this scheme does not rely on computational power to remain secure.

Benefits

Prevents single point-of-failure in key management.
Ensures operational security through mandatory multi-party participation.
Key rotation and share regeneration allows sustainable data security.
Secret disclosure can be audited as minimum number of shares need to be present at the same time.

Applications

Put simply, any situation that requires confidential information to be shared among multiple entities can use SSS. As I mentioned earlier, Vault uses this scheme to distribute a root key that protects your encryption key. But here are a few more security applications:

Distributed key management systems
Secure multiparty computation
Hardware security modules
Cryptocurrency wallet security

Security Considerations

Secure distribution of shares is crucial. Each share must be treated per information security best practices.
A true random (TRNG) or a good pseudorandom number generator (PRNG) must be used for coefficients.

Shamir's Secret Sharing Scheme

Table of contents