Selection Sort
 Nitin soni
Nitin soni
Selection Sort is a sorting method that picks the smallest number from the list and puts it at the front. It keeps doing this until the whole list is sorted.
Working of Selection Sort
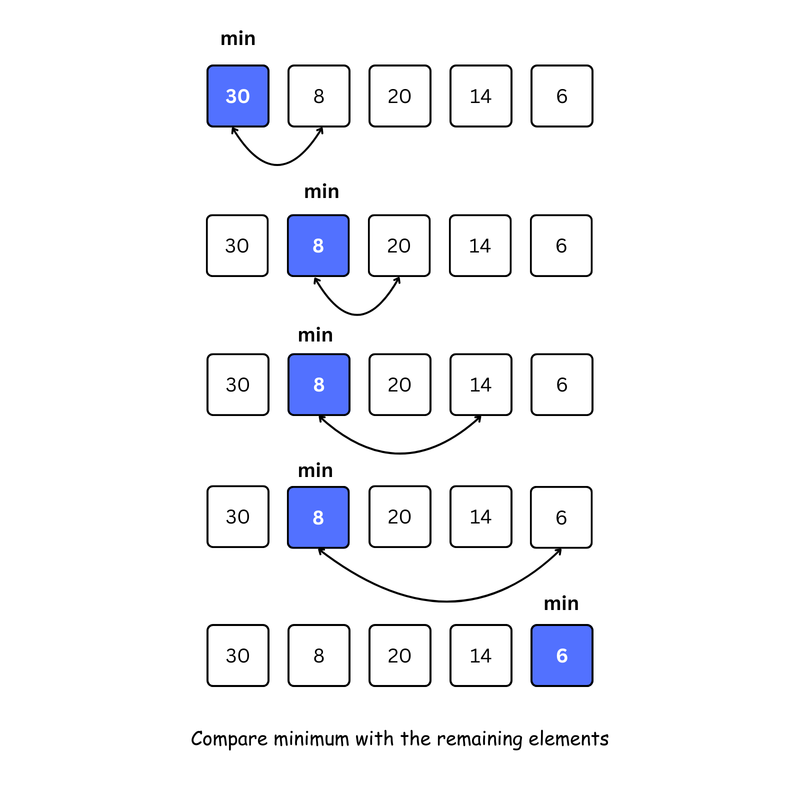
Compare
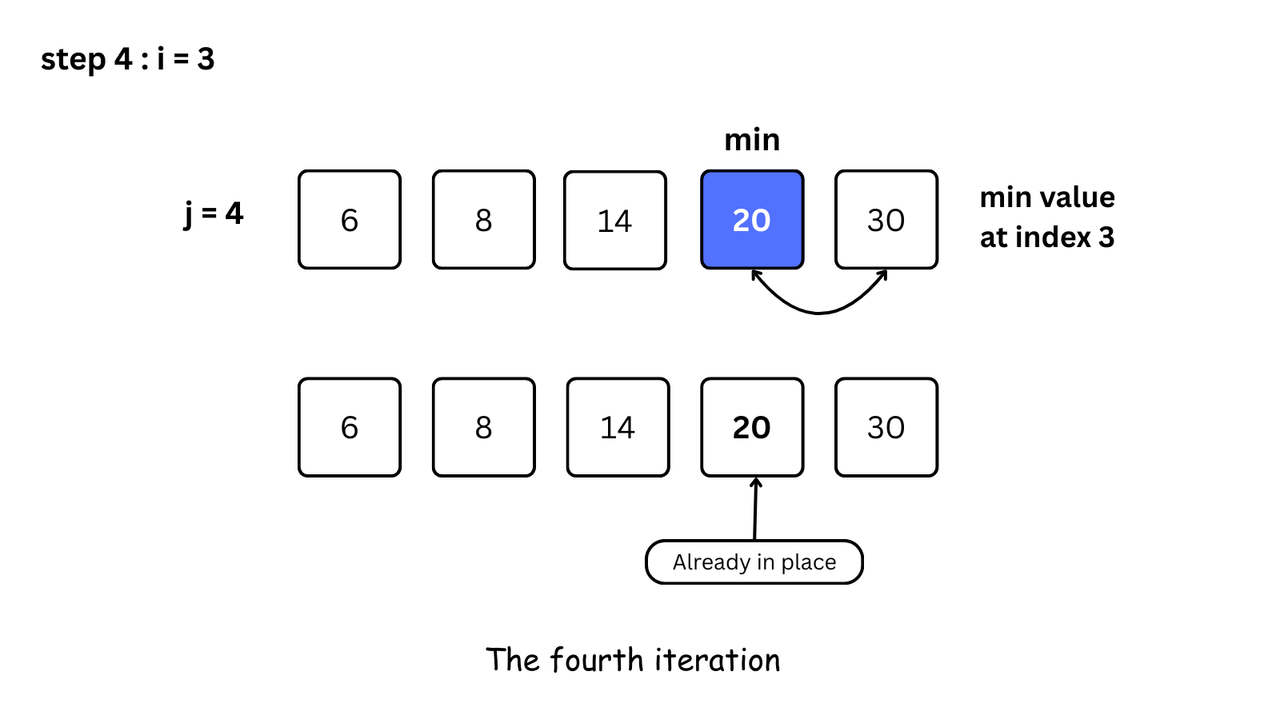
minimumwith the second element. If the second element is smaller thanminimum, assign the second element asminimum.
Compare minimum with the third element. Again, if the third element is smaller, then assign minimum to the third element otherwise do nothing. The process goes on until the last element.
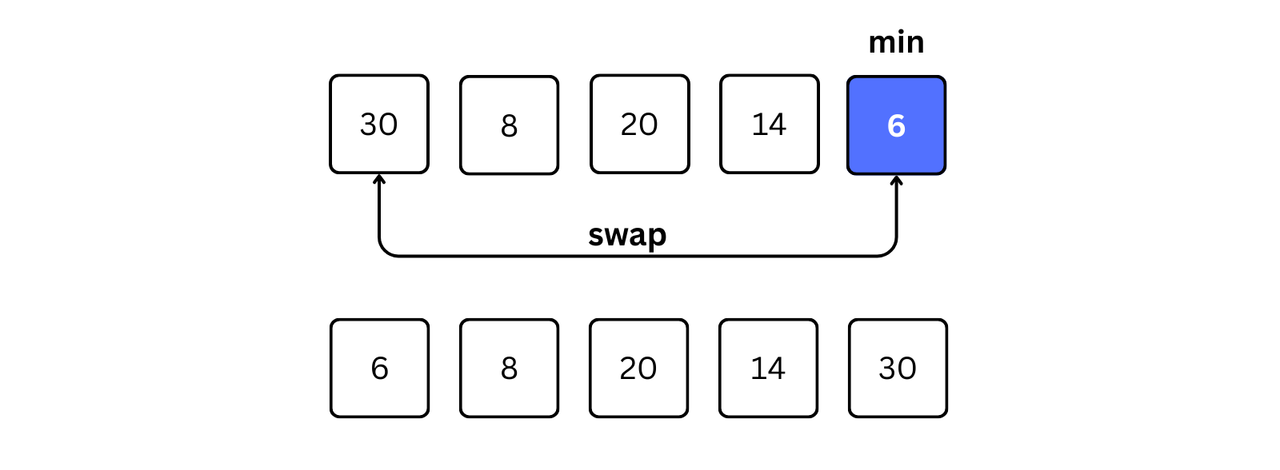
- After each iteration,
minimumis placed in the front of the unsorted list.
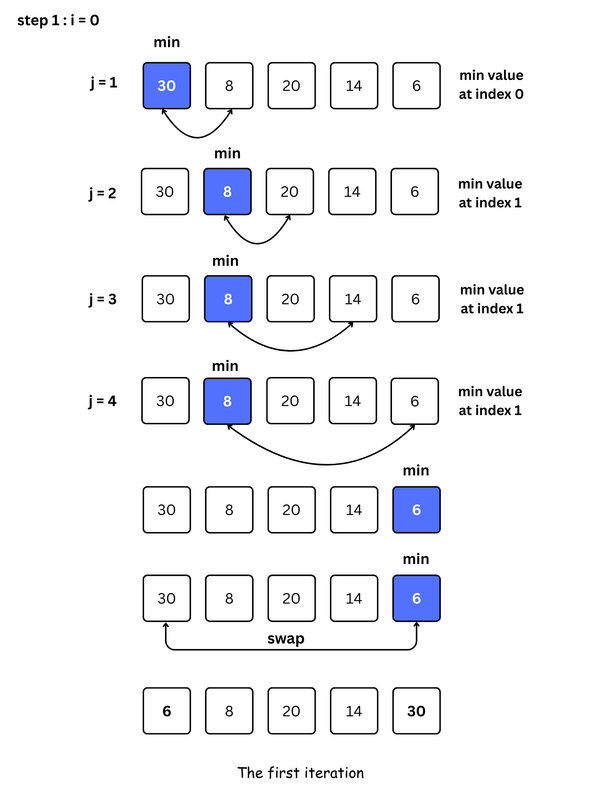
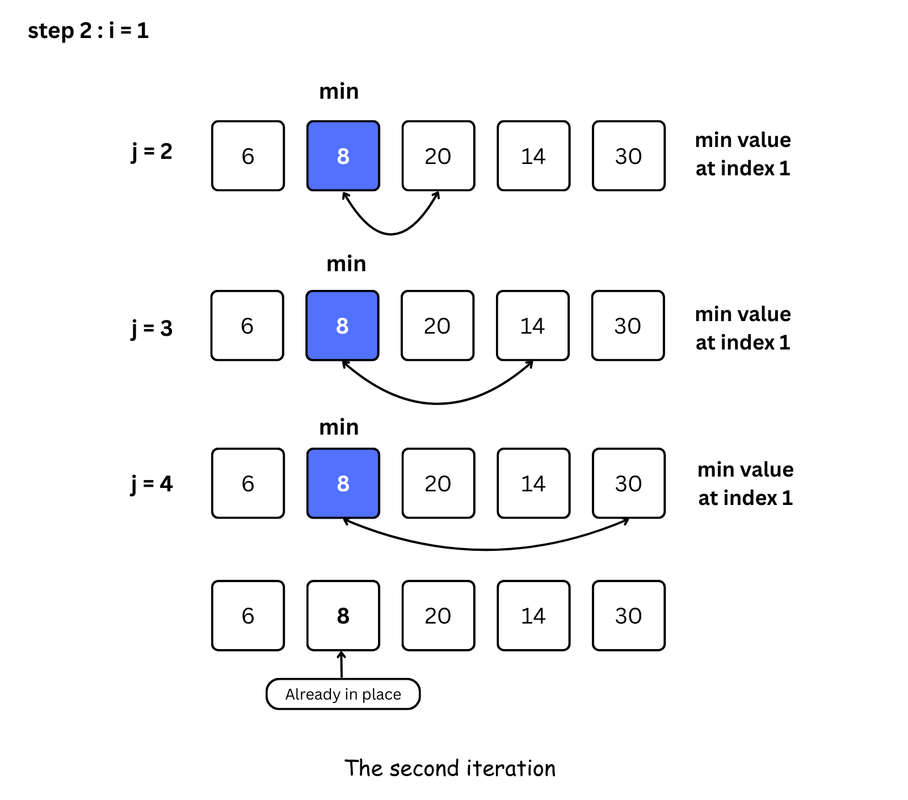
- For each iteration, indexing starts from the first unsorted element. Step 1 to 4 are repeated until all the elements are placed at their correct positions.
Selection Sort Algorithm
selectionSort(array, size)
for i from 0 to size - 1 do
set i as the index of the current minimum
for j from i + 1 to size do
if array[j] < array[current minimum]
set j as the new current minimum index
if current minimum is not i
swap array[i] with array[current minimum]
end selectionSort
Selection Sort code :
function selectionSort(arr) {
let n = arr.length;
for (let i = 0; i < n - 1; i++) {
let min = i;
for (let j = i + 1; j < n; j++) if (arr[j] < arr[min]) min = j;
[arr[i], arr[min]] = [arr[min], arr[i]];
}
return arr;
}
console.log(selectionSort([20, 12, 10, 15, 2]));
Selection Sort Complexity
| Time Complexity | |
| Best | O(n²) |
| Worst | O(n²) |
| Average | O(n²) |
| Space Complexity | O(1) |
| Stability | No |
Complexity in Detail
| Cycle | Number of Comparisons |
| 1st | (n-1) |
| 2nd | (n-2) |
| 3rd | (n-3) |
| ...... | ...... |
| last | 1 |
Hence, the number of comparisons is nearly equals to n2
(n - 1) + (n - 2) + (n - 3) + ..... + 1 = n(n - 1) / 2
Hence, Complexity: O(n²)
Also, if we observe the code, selection sort requires two loops. Hence, the complexity is n*n = n²
1. Time Complexities
Worst Case Complexity: O(n²) If we want to sort in ascending order and the array is in descending order then the worst case occurs.
Best Case Complexity: O(n²) It occurs when the array is already sorted
Average Case Complexity: O(n²) It occurs when the elements of the array are in jumbled order (neither ascending nor descending).
2. Space Complexity
- Space complexity is O(1) because an extra variable
minis used.
Selection Sort Applications
1. Small Data Sets
- When the dataset is very small (a few elements), the simplicity of selection sort can be an advantage.
- Example: Sorting top 5 scores in a game leaderboard.
2. Embedded Systems / Hardware-level Sorting
- Environments with limited memory or no recursion support, like:
- Microcontrollers
- Firmware
- Because it requires no extra space (in-place sorting).
3. Teaching and Learning
- Widely used in academic settings to introduce:
- Sorting logic
- Time complexity analysis
- Step-by-step understanding of algorithm design
4. Situations Where Swaps Are Costly
- Selection sort does fewer swaps compared to bubble sort.
- Useful when writing to memory is expensive (e.g., EEPROM, Flash).
5. Manual Sorting or Visualization
- Easy to visualize step-by-step for debugging or UI animations.
- Example: Coding interview platforms like LeetCode or HackerRank animations.
Subscribe to my newsletter
Read articles from Nitin soni directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Nitin soni
Nitin soni
Full stack developer