There are N courses, labelled from 1 to N.

We are given relations[i] = [X, Y], representing a prerequisite relationship between course X and course Y: course X has to be studied before course Y.

In one semester you can study any number of courses as long as you have studied all the prerequisites for the course you are studying.

Return the minimum number of semesters needed to study all courses. If there is no way to study all the courses, return -1.

Example 1:

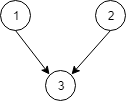
Input: N = 3, relations = [[1,3],[2,3]]
Output: 2
Explanation: 
In the first semester, courses 1 and 2 are studied. In the second semester, course 3 is studied.

Example 2:

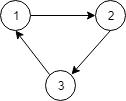
Input: N = 3, relations = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: 
No course can be studied because they depend on each other.

Note:

1 <= N <= 5000
1 <= relations.length <= 5000
relations[i][0] != relations[i][1]
There are no repeated relations in the input.

✅ 1. Problem Explanation (In Simple Terms)

You are given N courses (numbered 1 to N) and a list of prerequisite relations.
Each relation [X, Y] means: you must complete course X before taking course Y.

In a single semester, you can study as many courses as you want, as long as all their prerequisites are already done.

Your task is to return the minimum number of semesters required to finish all courses.

If there’s a cycle (like 1 → 2 → 3 → 1), it’s impossible to finish all courses → return -1.

💡 2. Key Insights

This is a Directed Graph problem:
- Courses = nodes
- Prerequisites = directed edges
You need to perform a level-wise topological sort:
- A node can be taken in the current semester if all its dependencies are met (in-degree == 0)
- Courses at the same level (with no dependencies) can be taken in the same semester
If there's a cycle, some courses will never reach in-degree 0 → we return -1.

🧠 3. Steps to Solve

Build a graph:
- Use an adjacency list to track dependencies
- Use an inDegree array to track how many prerequisites each course has
Topological Sort (BFS):
- Start with all courses that have inDegree = 0 (no prerequisites)
- In each semester:
  - Take all courses with inDegree = 0
  - Reduce the inDegree of their neighbors
  - If a neighbor’s inDegree becomes 0, it can be taken next semester
Track semesters:
- Each level in BFS = 1 semester
- If you finish all courses, return the semester count
- If not all courses are visited → cycle detected → return -1

✅ 4. JavaScript Code (Optimized & Well-Commented)

/**
 * @param {number} N - Total number of courses (1 to N)
 * @param {number[][]} relations - List of [X, Y] prerequisite pairs
 * @return {number} - Minimum number of semesters to complete all courses, or -1 if impossible
 */
function minimumSemesters(N, relations) {
  const graph = Array.from({ length: N + 1 }, () => []);
  const inDegree = Array(N + 1).fill(0);

  // Build the graph and in-degree count
  for (const [pre, next] of relations) {
    graph[pre].push(next);
    inDegree[next]++;
  }

  const queue = [];
  let semester = 0;
  let completed = 0;

  // Start with all courses that have no prerequisites
  for (let course = 1; course <= N; course++) {
    if (inDegree[course] === 0) {
      queue.push(course);
    }
  }

  // BFS level by level (each level = 1 semester)
  while (queue.length > 0) {
    const size = queue.length;
    semester++; // Start a new semester

    for (let i = 0; i < size; i++) {
      const course = queue.shift();
      completed++;

      for (const neighbor of graph[course]) {
        inDegree[neighbor]--;
        if (inDegree[neighbor] === 0) {
          queue.push(neighbor);
        }
      }
    }
  }

  // If we completed all courses, return semester count
  return completed === N ? semester : -1;
}

🔍 5. Dry Run Example

Input:

N = 3;
relations = [[1, 3], [2, 3]];

Graph:

1 → 3
2 → 3

Step-by-step:

In-degree:
- 1: 0
- 2: 0
- 3: 2
Semester 1:
- Courses with 0 in-degree → [1, 2]
- Take [1, 2]
- Decrease in-degree of 3 → 2 → 1 → 0
Semester 2:
- Courses with 0 in-degree → [3]
- Take [3]
All courses completed in 2 semesters ✅

⏱️ 6. Time Complexity

Let N be the number of courses, and E be the number of relations:

Graph Building: O(E)
Topological Sort BFS: O(N + E)

✅ Time Complexity: O(N + E)
✅ Space Complexity: O(N + E) for graph + in-degree array + queue

✅ Final Verdict

This is a topological sort using BFS (Kahn's Algorithm) with a twist: we count levels/semesters.
It's optimal and widely used in course scheduling/interview problems.
Handles cycles cleanly and efficiently.

Parallel Courses