Stacks and Queues

NachiketNachiket
8 min read

Table of contents

Introduction

As Android developers, our ability to manipulate data efficiently often determines the performance and scalability of our applications. While modern development frameworks provide numerous abstractions, a profound understanding of fundamental data structures remains essential for crafting optimal solutions to complex problems.

In this technical exploration, I'll dissect two critical data structures that form the backbone of countless algorithms: Stacks and Queues. Beyond merely defining their operations, we'll examine their internal mechanics, implementation variations, and practical applications with production-ready Java code examples.

1. Stack: The LIFO Powerhouse

1.1 Conceptual Framework

A stack operates on the Last-In-First-Out (LIFO) principle, or equivalently, First-In-Last-Out (FILO). This behavior mirrors common real-world scenarios, such as a stack of plates at a wedding buffet. You can only access the topmost plate; accessing plates beneath requires removing those above first.

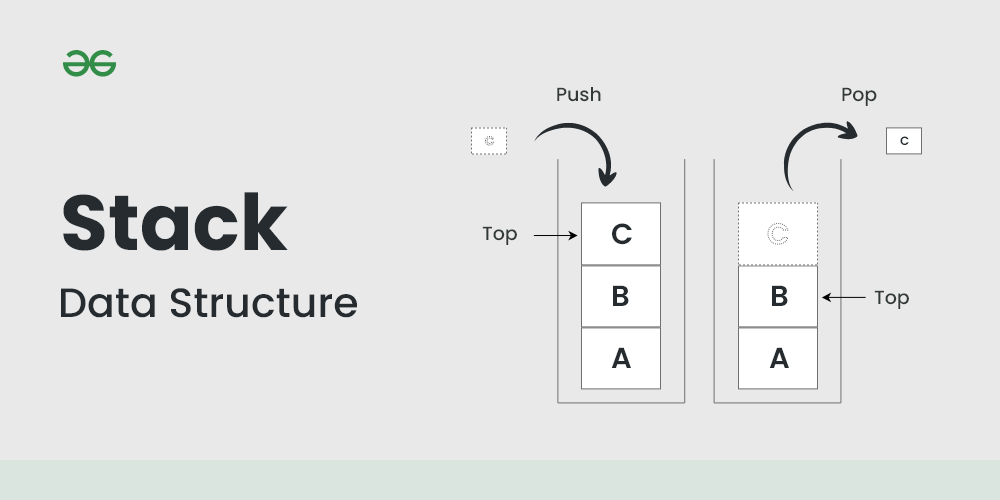
Stack Data Structure | GeeksforGeeks

1.2 Core Operations

Every stack implementation must support these fundamental operations:

  1. push(E item): Adds an element to the top of the stack

  2. pop(): Removes and returns the element at the top

  3. peek(): Returns but doesn't remove the top element

  4. empty(): Returns true if the stack contains no elements

1.3 Implementation

Java provides a Stack class in the java.util package, though the Deque interface offers a more versatile alternative for implementing stack behavior:

import java.util.Stack;
import java.util.ArrayDeque;
import java.util.Deque;

public class StackOperations {
    public static void main(String[] args) {
        // Using the Stack class (legacy approach)
        Stack<Integer> legacyStack = new Stack<>();

        // Using Deque as a stack (preferred modern approach)
        Deque<Integer> stack = new ArrayDeque<>();

        // Pushing elements
        stack.push(10);
        stack.push(20);
        stack.push(30);

        System.out.println("Stack: " + stack); // Output: Stack: [30, 20, 10]

        // Peek operation
        System.out.println("Top element: " + stack.peek()); // Output: Top element: 30

        // Pop operation
        System.out.println("Removed element: " + stack.pop()); // Output: Removed element: 30

        // Check if empty
        System.out.println("Is stack empty? " + stack.isEmpty()); // Output: Is stack empty? false

        // Current state
        System.out.println("Current stack: " + stack); // Output: Current stack: [20, 10]
    }
}

1.4 Implementation Considerations

While java.util.Stack extends Vector and is thread-safe, it suffers from performance penalties due to synchronization overhead. For most applications, using ArrayDeque as a stack provides better performance characteristics:

// Preferred implementation with superior performance
Deque<Integer> stack = new ArrayDeque<>();

// Legacy implementation (avoid unless thread safety is required)
Stack<Integer> stack = new Stack<>();

1.5 Exception Handling

Robust stack implementations should account for potential exceptions:

public class CustomStack<E> {
    private Deque<E> stack = new ArrayDeque<>();

    public void push(E item) {
        stack.push(item);
    }

    public E pop() throws StackException {
        if (stack.isEmpty()) {
            throw new StackException("Cannot pop from an empty stack");
        }
        return stack.pop();
    }

    public E peek() throws StackException {
        if (stack.isEmpty()) {
            throw new StackException("Cannot peek an empty stack");
        }
        return stack.peek();
    }

    public boolean isEmpty() {
        return stack.isEmpty();
    }

    public int size() {
        return stack.size();
    }
}

class StackException extends Exception {
    public StackException(String message) {
        super(message);
    }
}

2. Queue: The FIFO Foundation

2.1 Conceptual Framework

A queue implements the First-In-First-Out (FIFO) principle, or equivalently, Last-In-Last-Out (LILO). This behavior mimics real-world queuing systems, like customers waiting at a McDonald's counter, where the first person to arrive is the first to be served.

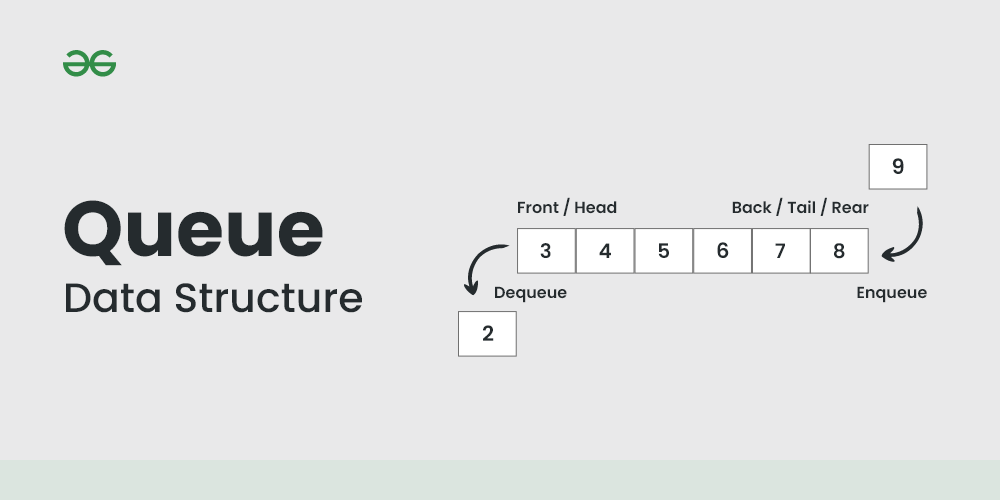
Queue Data Structure | GeeksforGeeks

2.2 Core Operations

Queues support these essential operations:

  1. add(E e)/offer(E e): Inserts an element at the tail of the queue

  2. remove()/poll(): Removes and returns the element at the head

  3. peek(): Returns but doesn't remove the element at the head

  4. isEmpty(): Returns true if the queue contains no elements

2.3 Java Implementation

Java provides the Queue interface with multiple implementations. The LinkedList implementation is commonly used because it optimizes the specific operations required by a queue:

import java.util.LinkedList;
import java.util.Queue;

public class QueueOperations {
    public static void main(String[] args) {
        // Initialize queue using LinkedList
        Queue<String> queue = new LinkedList<>();

        // Adding elements
        queue.add("Task 1");
        queue.offer("Task 2"); // Preferred when capacity is restricted
        queue.add("Task 3");

        System.out.println("Queue: " + queue); // Output: Queue: [Task 1, Task 2, Task 3]

        // Peek operation
        System.out.println("Head element: " + queue.peek()); // Output: Head element: Task 1

        // Remove operation
        System.out.println("Removed element: " + queue.remove()); // Output: Removed element: Task 1

        // Poll operation (safer alternative to remove)
        System.out.println("Polled element: " + queue.poll()); // Output: Polled element: Task 2

        // Current state
        System.out.println("Current queue: " + queue); // Output: Current queue: [Task 3]

        // Is empty check
        System.out.println("Is queue empty? " + queue.isEmpty()); // Output: Is queue empty? false
    }
}

2.4 Why LinkedList for Queue Implementation?

LinkedList is the preferred implementation for Queue because:

  1. It provides O(1) time complexity for adding elements at the end and removing from the front

  2. The internal doubly-linked structure enables efficient insertion and deletion at both ends

  3. Unlike array-based implementations, it doesn't require resizing or shifting elements

  4. It natively supports all operations defined in the Queue interface

2.5 Understanding Method Differences

Queue operations come in two forms:

  1. Throwing methods:

    • add(E e): Throws IllegalStateException if capacity is restricted

    • remove(): Throws NoSuchElementException if queue is empty

    • element(): Throws NoSuchElementException if queue is empty

  2. Non-throwing methods:

    • offer(E e): Returns false if addition is not possible

    • poll(): Returns null if queue is empty

    • peek(): Returns null if queue is empty

3. Deque: The Versatile Double-Ended Queue

3.1 Conceptual Framework

A Deque (Double-Ended Queue) represents a linear collection that supports element insertion and removal at both ends, combining functionality of both stacks and queues.

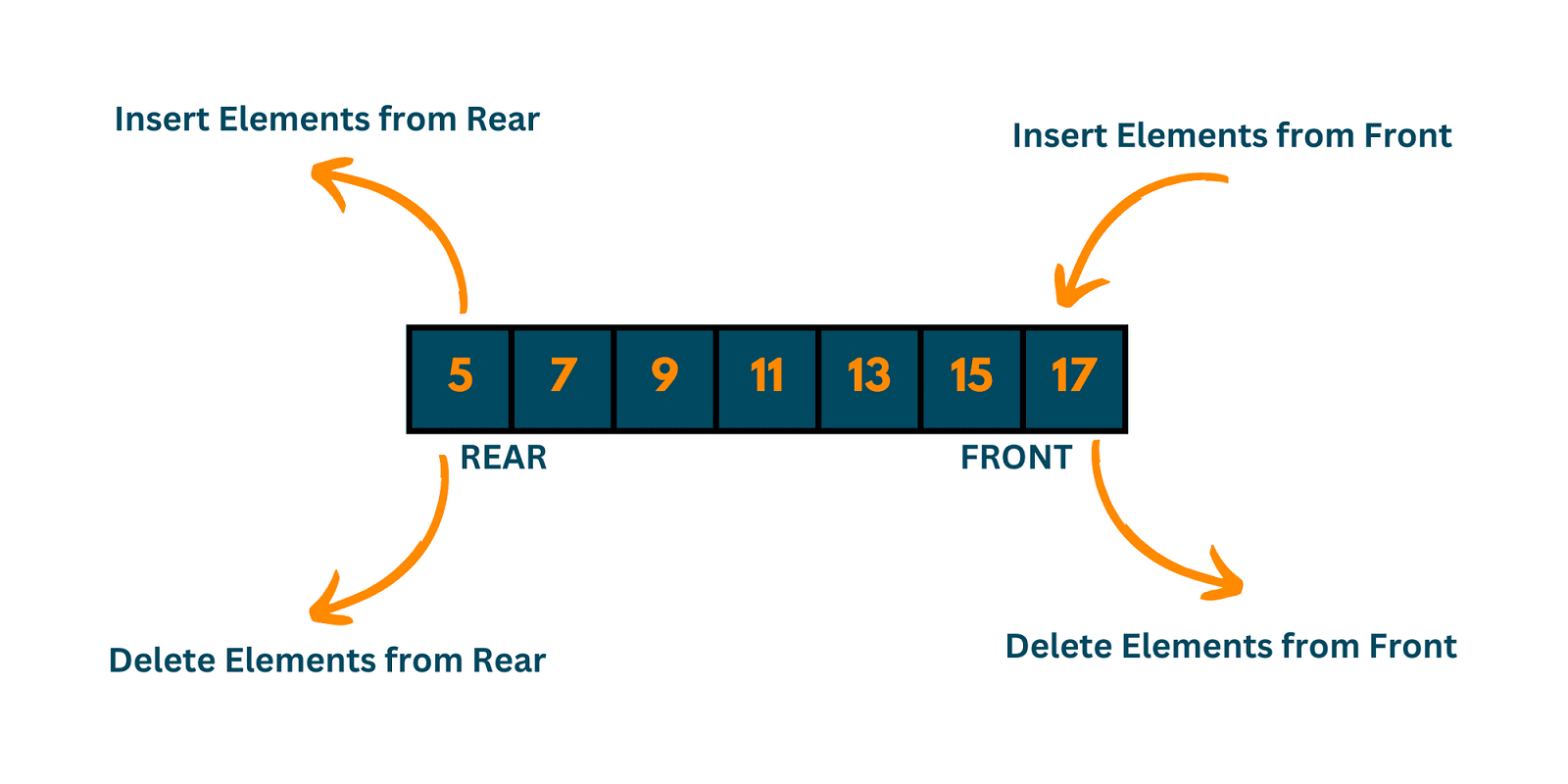
Understanding Python's deque | Python Central

3.2 Core Operations

Deques support an extended set of operations:

  1. Front operations:

    • addFirst(E e)/offerFirst(E e): Inserts at the front

    • removeFirst()/pollFirst(): Removes from the front

    • getFirst()/peekFirst(): Retrieves from the front

  2. Rear operations:

    • addLast(E e)/offerLast(E e): Inserts at the rear

    • removeLast()/pollLast(): Removes from the rear

    • getLast()/peekLast(): Retrieves from the rear

3.3 ArrayDeque Implementation

ArrayDeque provides a resizable array implementation of the Deque interface with no capacity restrictions:

import java.util.ArrayDeque;
import java.util.Deque;

public class DequeOperations {
    public static void main(String[] args) {
        // Initialize ArrayDeque
        Deque<Integer> deque = new ArrayDeque<>();

        // Front operations
        deque.addFirst(10);
        deque.offerFirst(20);

        // Rear operations
        deque.addLast(30);
        deque.offerLast(40);

        System.out.println("Deque: " + deque); // Output: Deque: [20, 10, 30, 40]

        // Access operations
        System.out.println("First element: " + deque.getFirst()); // Output: First element: 20
        System.out.println("Last element: " + deque.getLast());   // Output: Last element: 40

        // Removal operations
        System.out.println("Remove first: " + deque.removeFirst()); // Output: Remove first: 20
        System.out.println("Poll last: " + deque.pollLast());       // Output: Poll last: 40

        // Current state
        System.out.println("Current deque: " + deque); // Output: Current deque: [10, 30]
    }
}

3.4 ArrayDeque vs. LinkedList

ArrayDeque offers several advantages over LinkedList for most deque applications:

  1. Memory efficiency: Consumes less memory per element

  2. Locality of reference: Array-based structure improves cache performance

  3. Faster operations: Generally outperforms LinkedList for most operations

  4. No allocation overhead: Doesn't create separate node objects for each element

4. Circular Queue: The Efficient Cyclic Buffer

4.1 Conceptual Framework

A Circular Queue is a linear data structure where operations are performed based on FIFO principle, and the last position is connected to the first position to form a circle. It efficiently utilizes memory by reusing spaces.

Circular Queue in data structure - Shiksha Online

4.2 Core Operations

  1. enqueue(E e): Adds an element to the rear

  2. dequeue(): Removes an element from the front

  3. peek(): Returns the front element without removing it

  4. isFull(): Checks if the circular queue is full

  5. isEmpty(): Checks if the circular queue is empty

4.3 Java Implementation

Implementing a circular queue requires careful management of front and rear pointers:

public class CircularQueue<E> {
    private E[] elements;
    private int front;
    private int rear;
    private int size;
    private int capacity;

    @SuppressWarnings("unchecked")
    public CircularQueue(int capacity) {
        this.capacity = capacity;
        elements = (E[]) new Object[capacity];
        front = 0;
        rear = -1;
        size = 0;
    }

    public boolean enqueue(E item) {
        if (isFull()) {
            return false;
        }

        rear = (rear + 1) % capacity;
        elements[rear] = item;
        size++;
        return true;
    }

    public E dequeue() {
        if (isEmpty()) {
            return null;
        }

        E item = elements[front];
        elements[front] = null; // Help with garbage collection
        front = (front + 1) % capacity;
        size--;
        return item;
    }

    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return elements[front];
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public boolean isFull() {
        return size == capacity;
    }

    public int size() {
        return size;
    }
}

4.4 Using the Modulo Formula

The modulo operation (index % capacity) is crucial for circular queue implementation because:

  1. It enables wrap-around behavior when indices exceed array bounds

  2. It transforms a linear array into a conceptual circular structure

  3. It eliminates the need to physically shift elements when dequeuing

Example usage:

public class CircularQueueDemo {
    public static void main(String[] args) {
        CircularQueue<Integer> circularQueue = new CircularQueue<>(5);

        // Enqueue operations
        circularQueue.enqueue(10);
        circularQueue.enqueue(20);
        circularQueue.enqueue(30);
        circularQueue.enqueue(40);

        System.out.println("Front element: " + circularQueue.peek()); // Output: Front element: 10

        // Dequeue operations
        System.out.println("Dequeued: " + circularQueue.dequeue()); // Output: Dequeued: 10
        System.out.println("Dequeued: " + circularQueue.dequeue()); // Output: Dequeued: 20

        // Adding more elements (reusing the freed space)
        circularQueue.enqueue(50);
        circularQueue.enqueue(60);

        System.out.println("Front element after wrap-around: " + circularQueue.peek()); 
        // Output: Front element after wrap-around: 30
    }
}

Top LeetCode Problems I've Solved

  1. #232: Implement a Queue using Stacks

  2. #1863: Sum of All Subset XOR Totals

  3. #20: Valid Parentheses

  4. #921: Minimum Add to Make Parentheses Valid

GitHub Repository

For the complete implementation of these data structures along with additional optimizations and test cases, visit my GitHub repository:

https://github.com/QuantumPineapple68/DSA

Conclusion

Understanding stacks and queues at this fundamental level provides essential tools for solving complex algorithmic challenges. These data structures not only form the foundation for more advanced concepts but also offer elegant solutions to numerous real-world problems.

By mastering their implementations, variations, and application strategies, I've been able to solve numerous challenging problems across Android system architecture, background processing, and algorithmic optimizations in production applications.

What truly separates proficient developers from exceptional ones is the ability to select the right data structure for specific problem domains and implement it with attention to performance characteristics and edge cases.

10
Subscribe to my newsletter

Read articles from Nachiket directly inside your inbox. Subscribe to the newsletter, and don't miss out.

JavaqueuestackDSAdata structures

Written by

Nachiket
Nachiket