Step-by-Step Guide On Implementing Neural Networks From Scratch - Part 1

There are 3 things I’ll be covering in this article:

• Neural Networks and the Intuition behind them

• A Single Neuron

• Forward and Backward Propagation

What are Neural Networks and what’s the intuition behind them?

Ever wondered how modern AI like chatGPT, gemini and other complex AI models and algorithms work? Turns out when you break these problems down it all boils down to neural networks.

So what are neural networks anyway? To put it in layman terms they’re a bunch of individual neurons / nodes that are interconnected to each other and pass information among themselves.

The intuition behind neural networks is, as you might have already guessed, the neural structure of brains. Yes, they are inspired by biology. This is one of the rare cases where it’s easy to see that technology and biology, when combined, give birth to awesome results.

So first, let’s look at how the human brain works very briefly (yeah, we don’t want to go into too much detail there; it’s a mess).

Like I said, that looks like a mess, right? What you’re seeing right now is a very high-detailed mapping of a piece of the human brain. They are all neurons that are interconnected to pass information in our brain. At it’s core, a single neuron looks like this:

It takes a bunch of input from the left, processes it, and fires the output from the right.

This is exactly what inspired scientists to come up with the idea of creating neural networks, one of the most powerful algorithms to be developed.

Neural networks, at their core, work similarly to neurons in the brain. They have individual neurons that take in a bunch of input, process it, and pass the output to the next neuron. And these neurons are deeply connected with other neurons in the next layer helping them pass information.

Neural networks have 3 layers in them:

• Input Layer

• Hidden Layer

• Output Layer

The neurons take input from the input layer, process the input through the hidden layers, and pass the output to the output layer. Their flow chart, unsurprisingly, looks the same as the neuron diagram above.

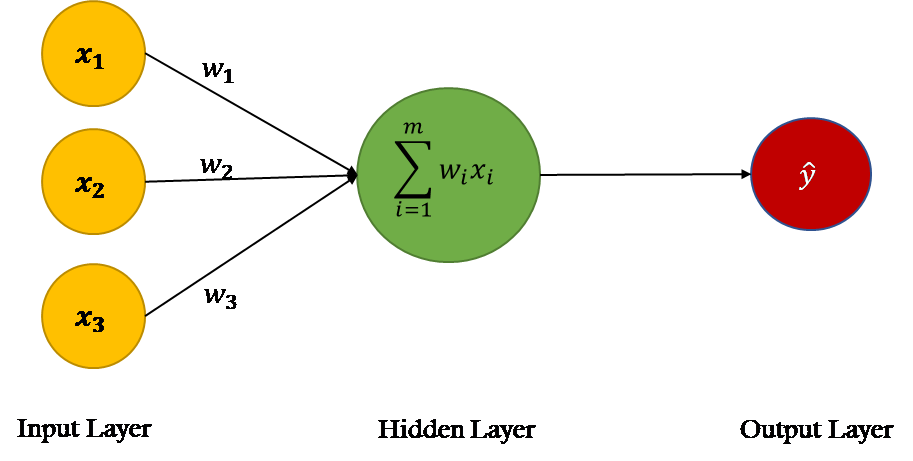
By training a bunch of hidden layers of neurons with unique weights and biases, we can create a complex network capable of solving complex problems. And here's an interesting point: While we understand the basic mechanics of how each neuron operates, the overall decision-making process of large networks is often difficult to interpret, making the system feel like a black box.

And that’s the basic outline of how neural networks came into existence and the intuition behind them.

Defining the problem

Let’s first define a problem and understand its input structure so we know what we’re working with. It is important to understand the problem first before trying to solve it (which seems obvious, but most people forget that fact).

The problem we’re going to solve in this article is the MNIST dataset, the 'Hello World' of neural networks.

The MNIST dataset is a famous dataset that contains around 60,000 examples of 28×28 grayscale (basically black and white) images of handwritten digits from 0-9, along with their labels. (Ah, if you’re having trouble keeping up with the terminology, make sure you read my previous articles, which will introduce you to most machine learning terms. They’re short and packed with information, so do give them a read.)

So let’s define the architecture of our neural network. As you know, it consists of 3 parts: the input layer—our pixels, the hidden layer—the actual network we’ll implement today, and the output layer—the final label that the network predicts.

Our input layer consists of 784 nodes / neurons (whoa, that’s a big number, but wait, let me explain). We have grayscale (black and white) images with a 28×28 resolution. Computers don’t understand pictures like we do; they can only process images as pixels. So, we’re going to send every single pixel as an input to the network. An image with a 28×28 resolution obviously has 784 pixels (courtesy of calculators).

Now, coming to the hidden layer part, we’re going to have 2 hidden layers with 128 neurons in the first layer and 64 neurons in the second layer to keep the network simple (I was too lazy to edit the image of the network architecture below, so I chose these numbers). (Fun fact: There’s no exact number of layers or neurons to use in a network; it’s all trial and error. But if you ever decide to develop these networks, know that the more complex the problem you’re trying to solve is, the more layers and neurons you need [the deeper the network needs to be]).

And the output layer is pretty simple. We are trying to predict the number from the image/pixel data, and there are only 10 possible options to choose from, as they are all single digits. So, we’ll create an output layer with 10 neurons, where each neuron will represent the probability of itself being the correct answer (we’ll dive more into this later in the chapter).

So let’s take a look at the architecture of our neural network:

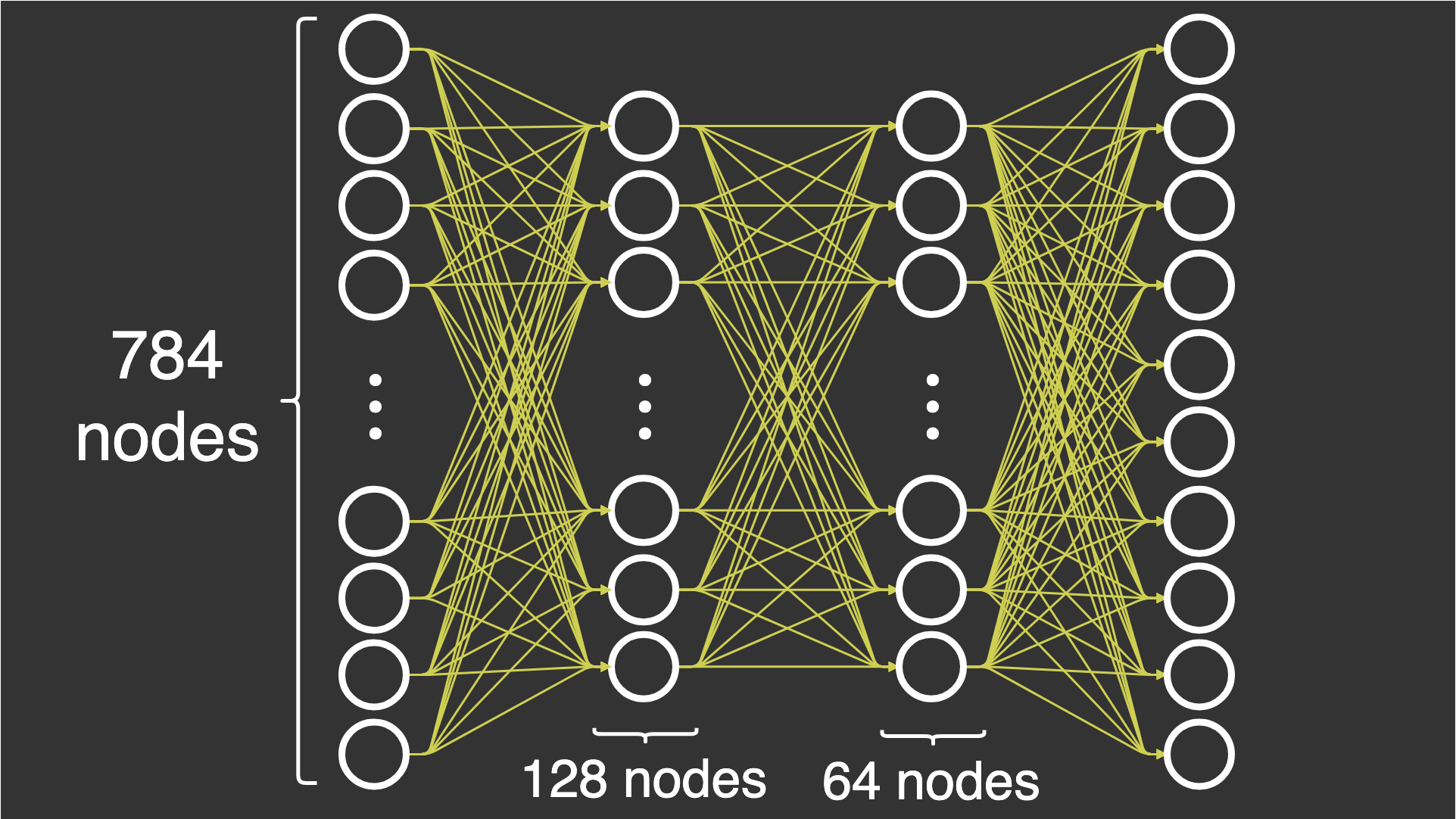
Pretty cool, right? Now that we know what we’re working with, let’s develop some intuition to be ready to implement a neural network from scratch in the next article.

We’re going to work with matrices rather than hardcoding the entire mathematical logic because it would be computationally expensive, and also because that’s how it’s done in the industry. (Though, if you want me to use for loops and variables to simplify it in a way that even high schoolers can understand, make sure to leave a comment below. I’ll try my best to do that in another article.)

So, the input looks like this: a matrix containing 60,000 rows and 784 columns, each row representing one image and each column representing one pixel. We’re going to flip things around to make it easier to compute later on. So, we’ll transpose our matrix, making each column represent one image (so it’s now 784 rows and 60,000 columns)

We are going to send each column as input to our network one at a time (since both the input layer and each column have the same number of nodes—784. Now you understand why we flipped it around, right? Think of it like pushing a line of 784 people, standing vertically like a column, off the train through one door—that's the input layer. There are 60,000 people, by the way.)

So, how does passing these inputs into the hidden layer give us the desired output, you ask? Well, that’s where we introduce weights and biases. Each neuron has a unique weight and bias associated with it. These weights are multiplied by the input and added to the bias to produce a new number (Spoiler alert: we’re going to refer back to a different article of mine to understand this), and that number is sent as input to the next layer. This manipulation of our input is obviously necessary to get a result from a given input.

So, who decides these weights and biases? That’s the magic—it’s the network itself that determines these weights and biases to get the accurate output. Our job, as lazy as it might sound, is to initialize these parameters (weights and biases) with random numbers. Yes, random.

We will create a pathway for our inputs to travel from the input layer to the output layer by passing through these hidden layers. After the first pass, we calculate the error and adjust our parameters to perform better next time. This can be viewed as something like gradient descent for updating the parameters. Learn more about it here.

Now, before we delve into how we pass the inputs and how the network works, let’s look at a single neuron at its core:

A single neuron consists to 2 main sections:

The linear section and the activation section, if you were to write it as an equation this is what it is:

$$Neuron \; = \; Linear + Activation$$

Linear Section

Now what does linear mean, as it’s name suggest and to some it might ring a few bells, it is the linear equation we use in mathematics.

$$y = mx + b$$

yeah here the m is the weights and b is the bias, as we’re dealing with matrices I will use uppercase as convention. So here is the accurate equation

$$Y = WX + b$$

b is a scalar value so it’s lowercase.

Activation Section

The activation function is a simple function that takes the output from the linear section and squashes it to a number between a range of [-1, 1], or [0, ∞].

How does it do it? There’s multiple functions that can help do that but I’m going to number a few

• Sigmoid function

• ReLU (Rectified Linear Unit)

• Tanh

The formulas for these will be explained in the math and implementation part in the next article.

(Fun fact: Neurons are also called perceptrons.)

Now let’s talk about how neural networks work. And how they solve complex problems.

There’s 2 steps involved in doing this:

• Forward Propagation

• Backward Propagation

Forward Propagation

As the name suggest, this step is about sending our inputs forward from input layer to output layer through hidden layer. Here’s how it works:

We start with the input layer, where each pixel of an image gets assigned to an input node. These inputs are then passed into the hidden layers. At each hidden layer, the inputs are multiplied by weights, added to a bias, and then passed through an activation function to produce an output. This process repeats at each layer until we reach the output layer, where the network gives its final prediction.

In simpler terms, forward propagation is like a relay race: the inputs start at the first layer, get passed through each layer, and ultimately reach the output layer where the network "decides" the result. This is how the network processes the data and makes predictions, and it’s the first step before we calculate any errors or update the parameters.

Backward Propagation

And as the name suggests (man, they sure kept everything simple), backward propagation, or backpropagation, is where the magic happens. It’s the process by which the network learns from its mistakes and adjusts itself to improve.

After forward propagation, the network has made a prediction, but it’s not always accurate. Backpropagation is used to calculate the error (the difference between the predicted output and the actual label) and then figure out how to reduce that error by adjusting the weights and biases.

Here’s how it works:

1. The error is calculated at the output layer.

2. This error is then "sent back" through the network, layer by layer, using the chain rule of calculus.

3. The network adjusts its weights and biases based on this error, making small tweaks that will help the network get closer to the correct output the next time.

Think of it like this: Imagine you're playing chess with your sibling, and you make a wrong move. Now, you need to whine loud enough for your sibling to let you change your move, and you happily adjust your previous move (only to lose to them in the end). That’s exactly what the network is doing.

In essence, backpropagation helps the network learn and improve over time, turning it into a model capable of making more accurate predictions.

Also, I do not own any of the pictures used above. If you have any issues with them, just contact me, and I’ll take them down.

Well, congratulation you made it this far. This is only about how neural network works, in the next article we’ll do the boring math and the implementation of neural network from scratch.

If you enjoyed this article, please consider buying me a coffee.