Phép Tích Chập - Convolution Trong CNN

Convolutional Neural Networks (CNN) là một loại mạng nơ-ron học sâu có khả năng học được các mẫu, các đặc trưng cục bộ trong dữ liệu. CNN được dùng rất phổ biến trong mảng thị giác máy tính. Giống như cái tên của nó, phần chính của một CNN chính là phép tích chập (convolution). Trong bài viết này chúng ta sẽ tìm hiều về phép tích chập và hiểu tại sao có thể trích xuất được những đặc trưng nhờ vào phép tính này.
Trước khi tìm hiều về phép tích chập (Convolution), ta cần nhắc lại một số kiến thức liên quan sau:

Hệ màu RGB

RGB là viết tắt của red, green, blue. Chính là ba màu chính của ánh sáng khi tách ra từ lăng kính. và đương nhiên khi trộn ba màu trên theo một tỷ lệ nhất định, ta có thể tạo thành những màu khác nhau.

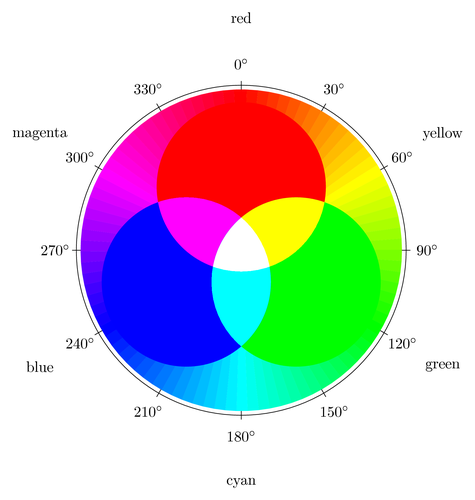
Nói cách khác thì một màu bất kỳ sẽ được biểu diễn bằng một bộ gồm ba số tương ứng là (r,g,b). Giá trị của của mỗi số sẽ là một số nguyên dương, nằm trong đoạn từ 0 đến 255. Trong đó (0,0,0) chính là màu trắng, (255, 255, 255) là màu đen. Như vậy với một phép tính đơn giản, ta có thể tính được tổng số màu mà bộ số này có thể tạo ra : $$256^3 = 16777216$$

Máy tính nhìn hình ảnh như thế nào?

Khi cần phải xử lý, chỉnh sửa hay chỉ đơn giản là tải ảnh từ một trang nào đó trên mạng về. Chắn chắc bạn sẽ để ý đến thông số của bức ảnh ấy, đặc biệt là kích thước ảnh. Ví dụ như bức ảnh về La Pedrera, Barcelona ở phía dưới đây có kích thước là 730 x 572

730 x 572 ở đây được tính theo đơn vị pixels (px). Có nghĩa là ảnh có chiều dài là 703 pixels và chiều rộng là 572 pixels.

Pixels (px) là đơn vị nhỏ nhất (một điểm ảnh) để tạo nên một bức ảnh kĩ thuật số. Hiểu đơn giản thì 1 pixel chính là một ô vuông rất nhỏ mang một màu duy nhất trong bức ảnh, việc kết hợp rất nhiều ô vuông (pixels) như vậy mang các màu giống hoặc khác nhau sẽ tạo nên một bức ảnh hoàn chỉnh.

Chính vì mỗi pixel mang trên mình một giá trị (r,g,b). Nên ta có thể biểu diễn
một hình ảnh như trên dưới dạng một ma trận có kích thước là 730 x 572. Dưới đây là ví dụ để bạn hình dung xem ma trận mà tôi nói đến trông như thế nào.

$$\begin{bmatrix} (255, 0, 0) & (0, 255, 0) & (0, 0, 255) \\ (122, 3, 42) & (200, 150, 100) & (50, 75, 125) \\ (122, 3, 42) & (200, 150, 100) & (50, 75, 125) \end{bmatrix}$$

Ma trận biểu diễn các giá trị màu RGB, trong đó mỗi phần tử là một bộ ba (R, G, B) với giá trị từ 0 đến 255

Để đơn giản hơn trong việc lưu trữ và tính toán cho sau này, chúng ta sẽ tách ma trân trên thành ba ma trận riêng biệt, mỗi ma trận tương ứng đại diện cho một màu trong ba màu R, G, B.

$$\begin{bmatrix}255 & 0 & 0 \\ 122 & 200 & 50 \\ 22 & 200 & 50 \end{bmatrix} \begin{bmatrix} 0 & 255 & 0 \\ 3 & 150 & 75 \\ 3 & 150 & 75 \end{bmatrix} \begin{bmatrix} 0 & 0 & 255 \\ 42 & 100 & 125 \\ 42 & 100 & 125 \end{bmatrix}$$

Các ma trận trên lần lượt biểu diễn giá trị của các kênh màu R (Red), G (Green), và B (Blue) được tách từ ma trận RGB ban đầu.

Ta cũng có thể biểu diễn lại ảnh trên bằng cách xếp chồng 3 ma trận R, G, B lên nhau tạo nên một tensor có kích thước 730 x 572 x 3 (Tensor là dạng dữ liệu có số chiều nhiều hơn 2)
Đương nhiên đây là trường hợp của ảnh màu. Với ảnh xám hay đen trắng ta chỉ cần một ma trận duy nhất để biểu diễn

Phép tính Element Wise giữa ma trận

Nhắc lại kiến thức toán, khi hai ma trận A và B cùng kích thước m × n ta có thể:
Cộng từng phần tử:

$$C_{ij} = A_{ij} + B_{ij}$$

Nhân từng phần tử:

$$C_{ij} = A_{ij}\times B_{ij}$$

Khác hẳn nhân ma trận (C=A × B), element-wise không thực hiện dot product giữa hàng và cột, mà chỉ nhân – cộng song song từng ô tương ứng.

Giả sử có hai ma trận cùng kích thước 2 × 3:

$$A = \begin{bmatrix} 2 & 5 & 1 \\ 4 & 3 & 7 \end{bmatrix} \quad B = \begin{bmatrix} 6 & 2 & 9 \\ 1 & 8 & 3 \end{bmatrix}$$

Nhân từng phần tử: C = A ⊙ B:

$$C_{ij} = A_{ij} \times B_{ij} \quad\Longrightarrow\quad C = \begin{bmatrix} 2 \times 6 & 5 \times 2 & 1 \times 9 \\ 4 \times 1 & 3 \times 8 & 7 \times 3 \end{bmatrix} = \begin{bmatrix} 12 & 10 & 9 \\ 4 & 24 & 21 \end{bmatrix}$$

Cộng từng phần tử: D = A + B:

$$D_{ij} = A_{ij} + B_{ij} \quad\Longrightarrow\quad D = \begin{bmatrix} 2 + 6 & 5 + 2 & 1 + 9 \\ 4 + 1 & 3 + 8 & 7 + 3 \end{bmatrix} = \begin{bmatrix} 8 & 7 & 10 \\ 5 & 11 & 10 \end{bmatrix}$$

Trong convolution ta sẽ sử dụng phép toán: C = A ⊙ B:

Phép tích chập - Convolution

Sau khi đã biết được máy tính xử lý hình ảnh như thế nào, thì ta sẽ đi vào chủ đề chính là phép tính Convolution. Điểm mấu chốt của phép tính này nằm ở những bộ lọc (Filter) hay còn gọi là kernel. Vì ảnh được biểu diễn mởi ma trận tên kernel cũng được định nghĩa là một ma trận vuông kích thước k*k (thường là 3 x 3, 5 x 5, ...) chứa các giá trị trọng số có thể cập nhật trong quá trình huấn luyện. Kernel ở đây cũng giống như weights trong bài toán Regression.
Dưới đây là một minh họa về cách hoạt động của convolution:

Kernel sẽ làm nhiệm vụ như một cái kính lúp đi chiếu qua từng ma trận con cùng kích thước với nó trong ảnh đầu vào và thực hiện phép tính element wise như đã nói ở trên cho hai ma trận. Nhưng để có thể trượt hay đi qua toàn bộ ảnh thì Kernel phải kết hợp cùng một tham số nữa là Stride. Như ở trên, ta thực hiện dịch chuyển (trượt) từng ô một trên ma trận thì Stride=1.

Đến đây có lẽ nhiều người sẽ đặt ra thắc mắc rằng, phép tính element wise sẽ cho ra kết quả là một ma trận có kích thước bằng với kích thước của 2 ma trận dùng để tính toán. Như trên ví dụ trên thì sẽ là ma trận 3 x 3 nhưng tại sao ở output chỉ có một giá trị duy nhất. Dù có một ma trận 3×3 trung gian, chúng ta không giữ lại nguyên ma trận ấy, mà nén nó thành một con số – đó chính là giá trị của feature map tại vị trí (i,j). Sau khi thi thực hiện tích chập thì ta sẽ thực hiện thêm một bước nữa đó là sum reduction, cụ thể là cộng tất cả giá trị trong ma trận kết quả lại. Nếu trong mạng nơ-ron thì sẽ có thêm tham số bias.

Vậy các kernel trích xuất đặc trưng trong ảnh như thế nào?

Trong quá trình học trong và cập nhật trọng số (các giá trị trong kernel) khi huấn luyện mạng nơ-ron sẽ từ từ tinh chỉnh các kernel bình thường ban đầu thành những kernel đặc thù để trích xuất được những đặc điểm hình dạng, đặc trưng của vật thể trong ảnh. Bạn có thể xem một số ví dụ về kernel bên dưới để hiểu rõ hơn.

Padding

Khi Kernel trượt hết các patch k × k “vừa vặn” trong ảnh, các pixel ở biên sẽ bị bỏ qua, làm feature-map thu được nhỏ hơn kích thước gốc.
Ví dụ: ảnh 5×5, kernel 3×3, stride = 1

$$W_{\text{out}} = \frac{5 - 3}{1} + 1 = 3$$

Ta có được feature-map 3×3

Để khắc phục việc mất thông tin ở các cạnh và (nếu cần) giữ nguyên kích thước đầu ra, ta dùng thêm một tham số nữa là zero-padding – đệm thêm các hàng/cột giá trị 0 quanh ảnh:

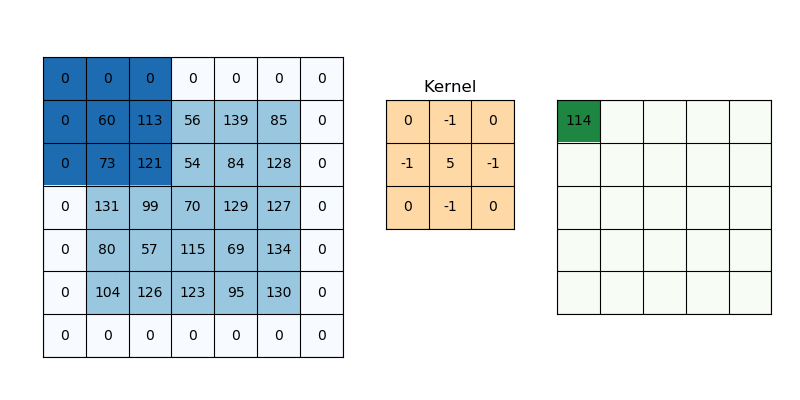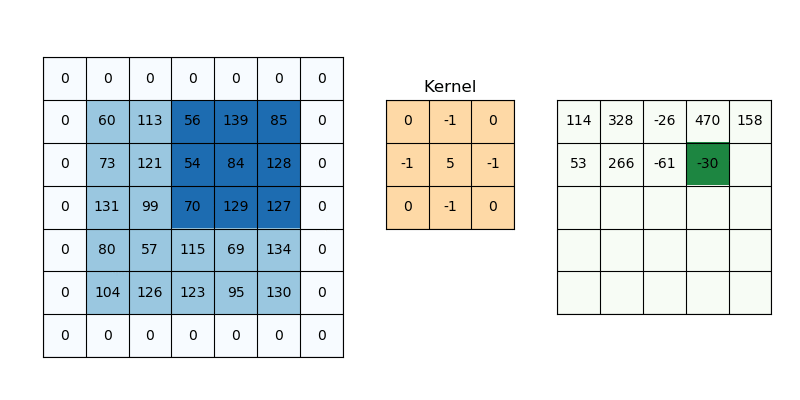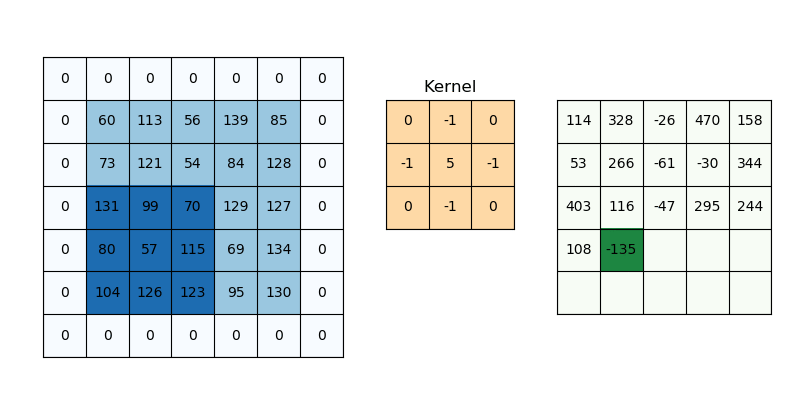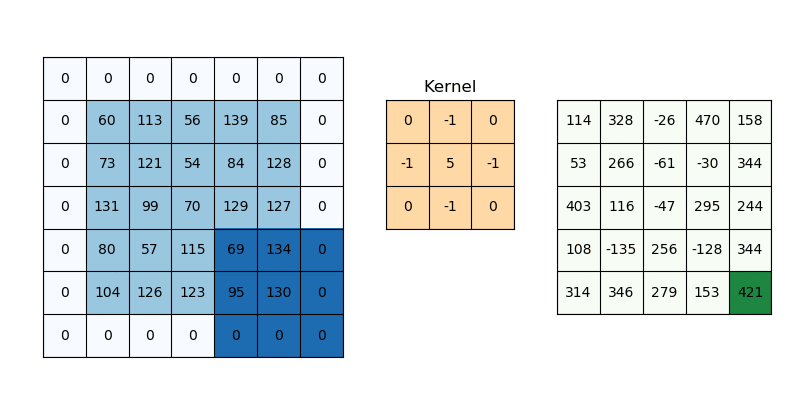
Như trên ví dụ ta dễ dàng thấy được:
Padding P = 1 (ảnh 5×5 → đệm thành 7×7), kernel 3×3, stride = 1:

$$W_{\text{out}} = \frac{5 - 3 + 2\cdot{1}}{1} + 1 = 5$$

Ta có được feature-map 5×5 (bằng với input)

Công thức chung cho kích thước feature-map:

$$W_{\text{out}} = \frac{W - k + 2P}{S} + 1,\quad H_{\text{out}} = \frac{H - k + 2P}{S} + 1$$