Exponentially Weighted Moving Averages in ML

In this post, I am going to pass on my understanding of moving averages.

I just learned it today, so there are possibilities of errors.

So, this is the basic formula of moving averages, but it does not look like an average. If you know the formula for taking an average of some numbers, then this formula does not look like any kind of average in the first place.

We will deconstruct this formula to make you understand how this works.

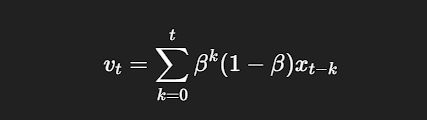
In this image, you can see this simple summation formula. When you open this summation, you get something like this.

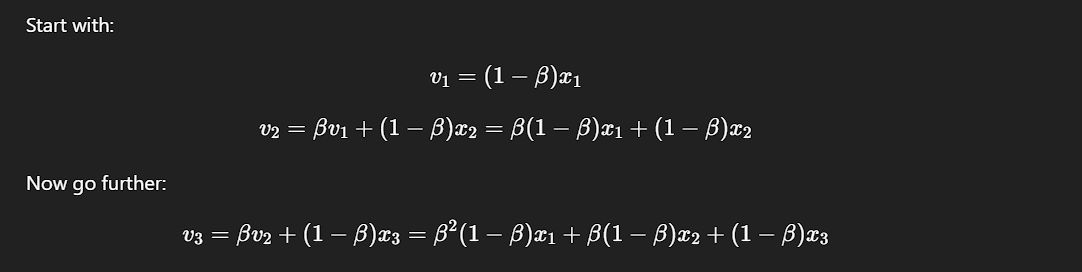
Now you can see this looks something like a formula for the average of some value.

You can see some pluses and the terms being weighted.

The older the term, the higher the degree of beta associated with that.

This beta is called the smoothing factor; its value generally lies between 0 and 1.

If you look at the general formula for any term of Exponentially Weighted Moving Averages, then you can see this beta.

The cool thing about this beta is that the higher its value, the more the possibility of the new value being closer to the previous one.

Think about it, it's obvious. You can also see it as if the value of beta is higher than, it takes a large chunk of the previous value and adds it to the new value.

So this was everything about the beta/ smoothing factor

Now, let's focus on the other aspects of this concept.

It's called exponentially weighted because when you open the formula and make it simpler, you can see that the terms previous to t are being weighted with higher powers of beta, which is increasing as we go to the right side of the equation, so in some sense you are exponentially weighting these early terms.

The reason it's called a moving average you are taking only the average of some specific value in a window and not all of the values. You can think of a window as something like a transparent rectangle moving over the list of values that you have, and the length of this transparent rectangle is equal to the number of values whose moving average you are calculating.

You can actually calculate how many days you are taking into your moving average by this formula.

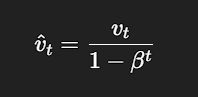
It's used in machine learning a lot. As far as I know, it's used in Gradient Descent Momentum, Adam algo, and RMSprop.

The cool thing about this formula is that as you go on finding larger or newer values, it starts to forget the older values, and the newer values will see more impact from the values closer to it than the values which are much farther to that "new value".

For instance, if you are calculating V20 then it's value will be affected more by V19 - V15 than values ranging from V5-V1, for the simple reason that the power of beta will increase a lot until V5 and as a result it will become very less than 0 which will scale down V5 and as a result its overall effect on V20. So, that's all from my side for today.