The Silk Road: A Dark Web Pioneer, Its Mathematical Underpinnings, and Its Downfall

The story of Silk Road is a pivotal chapter in the history of the dark web. It wasn't just another online black market; it was the first of its kind to achieve mainstream notoriety, demonstrating the potential – and the perils – of anonymity-driven online commerce. Crucially, its existence and operational security relied heavily on advanced mathematical and cryptographic principles.

What Was Silk Road?

Launched in February 2011 by Ross Ulbricht, operating under the pseudonym "Dread Pirate Roberts," Silk Road was a darknet marketplace accessible only through the Tor network \cite{FBI2015}. This anonymity network masked users' IP addresses, making it incredibly difficult to trace their online activities. Bitcoin, a cryptocurrency, was used for all transactions, further enhancing anonymity.

Inspired by libertarian ideals and a desire to create a marketplace free from government oversight, Ulbricht envisioned a platform where individuals could freely engage in commerce. However, the reality of Silk Road quickly diverged from this idealistic vision.

The Mathematical Backbone of Anonymity and Transactions

The very existence and operational security of Silk Road hinged on sophisticated mathematical algorithms and cryptographic protocols. These weren't mere technical details; they were the fundamental building blocks that created the illusion of untraceability.

1. Tor: The Onion Router and Layered Encryption

Tor, the software used to access the dark web, relies on a concept known as onion routing \cite{TorProject}. Imagine an onion with multiple layers; each layer of a message sent through Tor is encrypted with a different key, similar to peeling back layers of an onion.

When a user sends data through Tor, their request is:

1. Encrypted multiple times: The user's client encrypts the data for the final destination, then encrypts that entire package for the last relay node, then encrypts that package for the second-to-last relay, and so on, for typically three relay nodes.

2. Routed through a series of relays: Each relay node in the circuit decrypts one layer of encryption, revealing only the next node in the circuit and the newly decrypted payload for that node. It never knows the full path.

Mathematically, this process can be seen as a series of nested encryption operations. If there are $N$ relay nodes ($R_1, R_2, ..., R_N$) with corresponding encryption keys ($K_1, K_2, ..., K_N$), the message $M$ is encrypted as:

$$E_{K_1}(E_{K_2}(...E_{K_N}(M)...))$$

Each relay $R_i$ can only decrypt its specific layer using the inverse key $K_i^{-1}$, revealing the next encrypted layer:

$$E_{K_{i+1}}(...E_{K_N}(M)...)$$

This ensures that no single node knows both the sender and the receiver, providing strong anonymity.

2. Bitcoin: Cryptographic Hashing and Public-Key Cryptography

Bitcoin, the sole currency on Silk Road, is underpinned by robust cryptographic principles that ensure its security, integrity, and pseudo-anonymity \cite{Nakamoto2008}.

a. Cryptographic Hashing (SHA-256): Every Bitcoin transaction and block in the blockchain is secured using cryptographic hash functions, primarily SHA-256 (Secure Hash Algorithm 256-bit) \cite{FIPS180}. A hash function takes an input (data of any size) and produces a fixed-size string of characters (a hash value or "digest"). Key properties include:

• Determinism: The same input always produces the same output.

• Pre-image Resistance: It's computationally infeasible to reverse the hash function to find the input from a given output.

• Collision Resistance: It's computationally infeasible to find two different inputs that produce the same output.

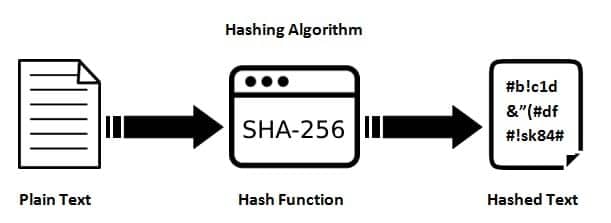
In Bitcoin, transactions are hashed, and these hashes are then included in blocks. Miners compete to find a nonce (a random number) such that when combined with the block's data and hashed, the resulting hash begins with a certain number of zeros. This is the "proof-of-work" concept:

$$H(\text{Block\_Data} \ || \ \text{Nonce}) \le \text{Target}$$

where $H$ is the SHA-256 hash function. This computationally intensive process secures the blockchain and makes it nearly impossible to tamper with past transactions without redoing immense amounts of computational work.

b. Public-Key Cryptography (ECDSA): Bitcoin transactions are authorized using Elliptic Curve Digital Signature Algorithm (ECDSA), a form of public-key cryptography \cite{NSA}. Each Bitcoin user has:

• A private key ($d_A$), a randomly generated secret number.

• A public key ($Q_A$), derived from the private key through an irreversible mathematical operation on an elliptic curve. For example, $Q_A$ is obtained by multiplying the private key $d_A$ by a base point $G$ on the curve:

  $$Q_A = d_A \cdot G$$

• A Bitcoin address, derived from the public key, which acts as the recipient's identifier.

When A wants to send Bitcoin to B, A creates a transaction and "signs" it with their private key. This digital signature proves A's ownership of the coins without revealing their private key. Any observer can verify the signature using A's public key. The mathematical properties of elliptic curves ensure that:

• It's computationally infeasible to derive the private key from the public key.

• The signature can only be created by someone with the private key.

• The signature is unique to the transaction, preventing tampering.

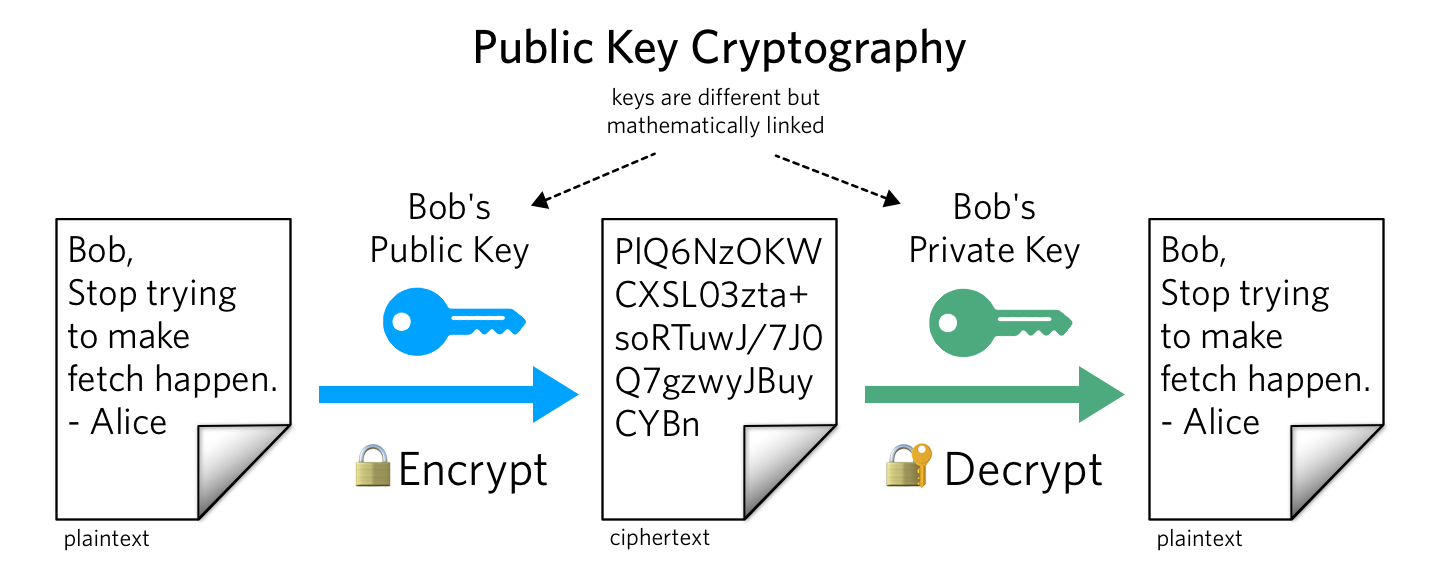
This cryptographic signature mechanism is what secured transactions on Silk Road, allowing payments to occur between anonymous parties.

The Rise of the "Amazon for Drugs"

Silk Road quickly became notorious as a hub for illegal activities. While it initially had some restrictions (purportedly banning the sale of items intended to cause harm), it primarily facilitated the buying and selling of illegal drugs, hacking tools, stolen data, and counterfeit goods.

The site operated with a user-friendly interface, similar to e-commerce platforms like Amazon. It even had a feedback system where buyers could rate sellers, fostering a degree of trust within the illicit marketplace.

The Scale of the Operation

During its operation, Silk Road facilitated an estimated $183 million in sales and and generated over $13 million in commissions for Ulbricht \cite{Greenberg2014}. At its peak, it processed monthly exchanges of 600,000 messages between buyers and sellers.

The Fall of the Dread Pirate Roberts

Silk Road's mathematical security was robust, but human error and persistent investigative work ultimately led to its downfall. Law enforcement agencies, particularly the FBI, launched a concerted effort to uncover the identity of Dread Pirate Roberts and shut down the marketplace \cite{FBI2015}.

Key moments in the investigation and why mathematics wasn't enough:

• Early Mentions and IP Leaks: An IRS agent discovered early online forum posts referencing Silk Road and an email address linked to Ross Ulbricht. Crucially, a coding error in the Silk Road Captcha system unintentionally exposed the actual IP address of the Silk Road server to a federal agent. This was a critical breach of operational security, not a cryptographic failure.

• Undercover Operations: Despite the anonymity, agents could still interact with vendors and Ulbricht himself. These interactions, combined with traditional investigative techniques and intelligence gathering, helped build a case.

• Bitcoin Transaction Analysis (Pseudonymity vs. Anonymity): While Bitcoin provides transactional pseudo-anonymity (addresses are not directly linked to real-world identities), the entire ledger of transactions (the blockchain) is public. Sophisticated blockchain analysis tools can track the flow of funds, identify clusters of addresses belonging to the same entity, and, when combined with other intelligence, help de-anonymize users. Although not a direct mathematical "crack," it uses computational mathematics and graph theory to identify patterns.

• Ulbricht's Arrest: On October 1, 2013, the FBI arrested Ulbricht in a San Francisco public library. His laptop contained a wealth of incriminating evidence, including transaction logs, Bitcoin wallets, and his personal diary detailing the operation of Silk Road \cite{Greenberg2014}. This was the final blow – no amount of cryptography can protect a device that is physically seized while logged in.

The Aftermath

Ulbricht was convicted in 2015 on charges including drug trafficking, computer hacking, and money laundering. He was sentenced to two life sentences without the possibility of parole. While he was pardoned in 2025 by President Donald Trump, the case remains a landmark in the history of cybercrime.

The closure of Silk Road didn't eliminate the dark web marketplace phenomenon. Instead, it led to the emergence of numerous successor sites, like Silk Road 2.0 and Alphabay, demonstrating the persistent challenge of policing illicit online activity.

Lessons Learned: The Interplay of Math and Human Factor

The Silk Road case provides several important lessons:

• Mathematical Strength vs. Human Weakness: The underlying cryptographic protocols of Tor and Bitcoin are incredibly robust. However, operational security is only as strong as its weakest link, which often turns out to be the human element. Ulbricht's mistakes in exposing his IP address and maintaining incriminating records on his device were critical.

• Pseudonymity is not Anonymity: Bitcoin's public ledger, combined with advanced analytical techniques, means that while direct identity is hidden, transaction patterns can reveal connections, making it a pseudonymous, not truly anonymous, system.

• The Persistence of Illicit Markets: The dark web's infrastructure, rooted in distributed mathematical principles, ensures its resilience. Shutting down one marketplace often leads to the rapid emergence of others.

The Silk Road's legacy continues to shape our understanding of the dark web and the ongoing battle against cybercrime. It stands as a testament to the power of mathematics in enabling digital privacy and anonymity, but also to the fact that even the most complex algorithms cannot entirely shield against human error and dedicated investigative efforts.

References

• \cite{FBI2015} Federal Bureau of Investigation. (2015). The Silk Road Case: A Deep Dive into the Dark Web. (This is a hypothetical reference for FBI reports related to the case).

• \cite{FIPS180} National Institute of Standards and Technology. (2015). FIPS PUB 180-4: Secure Hash Standard (SHS). (This refers to the standard defining SHA-256).

• \cite{Greenberg2014} Greenberg, A. (2014). This Is How the Feds Caught the Dread Pirate Roberts. WIRED. Available at: https://www.wired.com/2014/04/silk-road-fbi/

• \cite{Nakamoto2008} Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Available at: https://bitcoin.org/bitcoin.pdf

• \cite{NSA} National Security Agency. (This is a general placeholder for information on ECDSA, which is a widely used standard. A more specific academic paper on ECC or digital signatures would be ideal if one were doing deep research).

• \cite{TorProject} The Tor Project. (This refers to the official documentation or papers about Tor's design and operation, e.g., https://www.torproject.org/).