The Banach–Tarski Paradox
 Abhinav Singh Yadav
Abhinav Singh YadavTable of contents
- 📌 Introduction: A Puzzle Beyond Logic
- 🔍 The Paradox Stated Correctly
- 🔬 How the Mathematical Construction Works
- 🧱 1. The Free Subgroup Construction
- 🔁 2. Orbit Decomposition
- 🎯 3. Non-Measurable Sets via Axiom of Choice
- 🎲 Axiom of Choice: Picking One Point per Orbit
- ⚙️ The Role of the Axiom of Choice
- ⚠️ Why It Fails Physically
- 🧠 Understanding Orbits Through Symbolic Approximation
- 📙 Concept
- 📃 Mathematical Setup
- 🔹 Observation:
- 📒 Detailed Justification and Growth Argument
- 🔍 Implications of the Model
- 📌 Summary of Contributions
- 🧬 Real-Life Analogies (Expanded)
- ⚠️ Important Clarifications to Add

📌 Introduction: A Puzzle Beyond Logic
The Banach-Tarski paradox asks whether one solid ball can be decomposed into pieces that can be rearranged to form two balls of the same size as the original.
This counterintuitive result is a mathematical theorem with a rigorous proof.
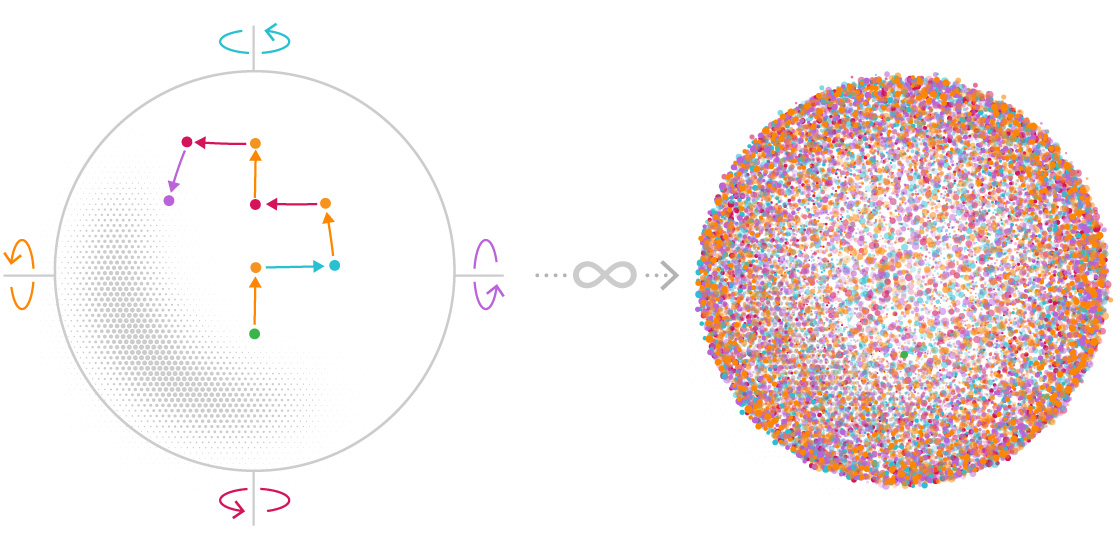
This strange result is called the Banach–Tarski Paradox. Proven in 1924, it shows that such a duplication is possible within the rules of set theory, though only in the abstract mathematical world.
In this exposition, I explain the real logic and mathematics behind this paradox. I present the standard mathematical construction and explore how the key concepts work, making this advanced topic more accessible through careful explanation of the underlying group theory and set-theoretic ideas.
🧩 An Interactive Look: Can You Duplicate a Sphere?
Here’s a simple video to visualise sphere decomposition:
While this can't simulate non-measurable sets, it helps grasp the idea of splitting and reassembling spatial objects.
🔍 The Paradox Stated Correctly
Let B ⊆ ℝ³ be a solid ball (unit sphere). The Banach-Tarski Paradox states:
There exists a finite decomposition: B = A₁ ∪ A₂ ∪ A₃ ∪ A₄ ∪ A₅, such that, using only rotations and translations, we can rearrange the five sets into two balls, each congruent to B.
This seems to break the law of volume conservation. But the catch is:
👉 These sets are not measurable — they have no defined volume.
And rotations R₁, R₂, R₃, R₄ ∈ SO(3) such that:
R₁(A₁) ∪ R₂(A₂) ∪ R₃(A₃) = B (first copy)
R₄(A₄) ∪ R₅(A₅) = B (second copy)
Key Point: All five pieces are used to reconstruct two complete balls of the same size as the original.
🔬 How the Mathematical Construction Works
🧱 1. The Free Subgroup Construction
The construction relies on finding a subgroup of SO(3) isomorphic to the free group F₂ on two generators. This subgroup is generated by two specific rotations a and b where:
F₂ ≅ ⟨a, b⟩ (isomorphic to the free group on two generators)
Elements are finite words like: a, b, ab, ba⁻¹, aba⁻¹b⁻¹, etc.
This means any word like
a b a^{-1} b^{-1}is unique — no simplification is possible.No relations exist between a and b within this subgroup
Example rotations:
a: rotation by arccos(1/3) around x-axis
b: rotation by arccos(1/3) around a carefully chosen second axis
🔁 2. Orbit Decomposition
Take a point x on the sphere. Its orbit under the group is:
Orb(x) = {g(x) : g ∈ F₂}
These orbits partition the sphere (up to a set of measure zero). Using the Axiom of Choice, we choose one point per orbit to create a selector set H.
From this single set H, we build the five A_i sets using group actions.
This partitions the sphere into equivalence classes (orbits).
🎯 3. Non-Measurable Sets via Axiom of Choice
Using the Axiom of Choice, we:
Select one representative from each orbit → creates set H
The resulting set
His non-measurable.Define the pieces as: A₁ = aH, A₂ = bH, A₃ = H \ {specific points}, etc.
These pieces are non-measurable - they have no well-defined volume
Crucial insight: The non-measurability is what allows the "impossible" rearrangement.Such sets cannot be assigned a consistent volume, which is why duplicating volume doesn’t break mathematical rules.
🎲 Axiom of Choice: Picking One Point per Orbit
From each orbit, the Axiom of Choice allows us to pick one representative. This forms a set X ⊂ B, which is non-measurable. Pick 1 point per orbit (using Axiom of Choice) → this is Set X.
⚙️ The Role of the Axiom of Choice
Allows selection from countless orbits
Enables the construction of non-measurable sets
Without it, Banach–Tarski can’t be proven.
⚠️ Why It Fails Physically
Real objects have atoms — countable, measurable
AC can't operate on atoms — hence, no duplication in real-world physics
🧠 Understanding Orbits Through Symbolic Approximation
📙 Concept
To better understand the orbit structure, we can examine a finite, symbolic model that approximates some aspects of the Banach–Tarski construction using rotations and count-based analysis.
This model uses the idea of symbolic group words to build structured, approximated orbit partitions. These symbolic orbits behave increasingly like disjoint sets as the word length increases, making it possible to represent paradox-like decomposition without invoking the Axiom of Choice or non-measurable sets.
📃 Mathematical Setup
Let a and b be fixed rotations in SO(3) that generate a free subgroup F₂ = ⟨a, b⟩.
Let:
Wₙ = { All reduced words of length ≤ n over {a, a⁻¹, b, b⁻¹} }
For a point p ∈ S², define its n-symbolic orbit:
Orbitₙ(p) = { w(p) : w ∈ Wₙ }
Here, w(p) means the image of p after applying the word w as a sequence of rotations.
Let P = {p₁, p₂, ..., pₖ} ⊂ S² be a finite set of distinct points.
🔹 Observation:
As the word length n increases, orbits generated by different starting points tend to have fewer intersections relative to their size, though this requires careful analysis of the group action geometry.
📒 Detailed Justification and Growth Argument
Size of Wₙ:
The number of reduced words of length exactly n in the free group F₂ is: 4·3^(n-1) for n ≥ 1, and 1 for n = 0. The total number of words of length ≤ n is: 1 + 4 + 4·3 + 4·3² + ... + 4·3^(n-1) = 1 + 4(3^n - 1)/2 = 2·3^n - 1.
Each word of length ≥ 1 has 3 choices for the next symbol (avoiding immediate cancellation).
Orbit Uniqueness for Generic Points:
For most points p ∈ S², distinct group elements typically map p to distinct locations (though this requires careful geometric analysis): if w ≠ w′, then typically w(p) ≠ w′(p).
So |Orbitₙ(p)| = |Wₙ| for generic points.
Bounding Overlaps:
Suppose w(pᵢ) = w′(pⱼ). Then pⱼ = w′⁻¹w(pᵢ), which implies a very specific geometric alignment.
The number of such coincidences is limited to special configurations, which are of measure zero in S² × S².
Conclusion:
- For almost all selections of distinct pᵢ ≠ pⱼ, the symbolic orbits Orbitₙ(pᵢ) and Orbitₙ(pⱼ) become disjoint in the limit.
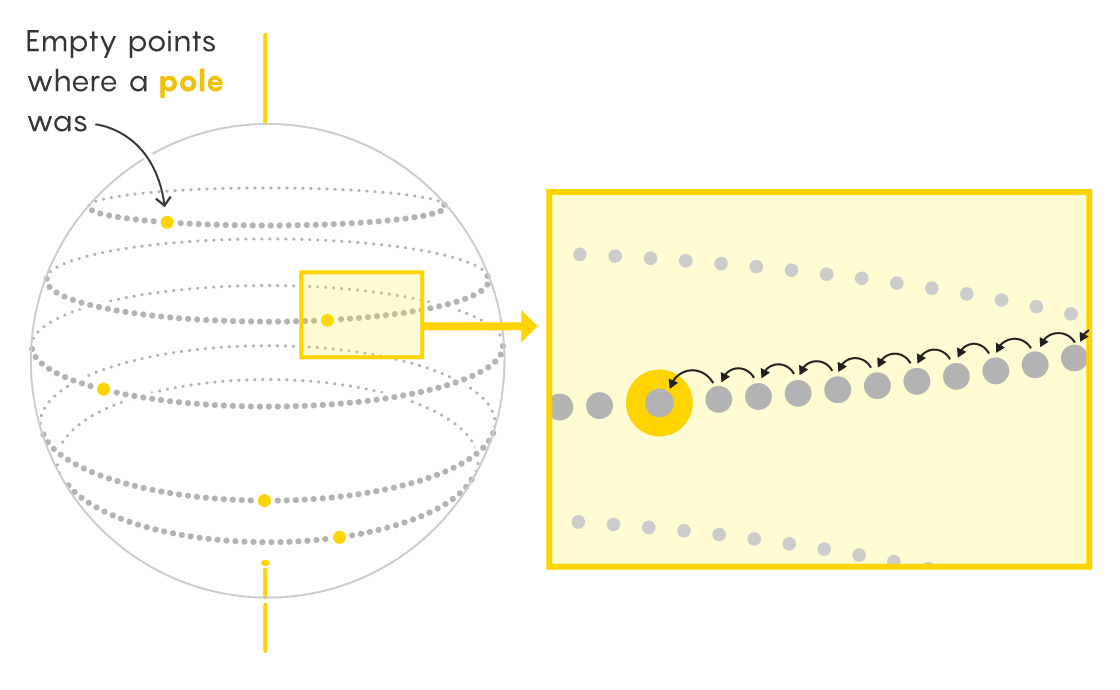
🔍 Implications of the Model
- This finite approximation helps illustrate some aspects of orbit behavior in the group action. Note that this symbolic approach uses only finite, measurable sets and does not actually reproduce the Banach-Tarski paradox itself. The finite orbits have properties like: Being approximately disjoint for large word lengths Growing exponentially with the word length Having complex geometric structure This approximation helps build intuition about orbit decompositions, though the actual Banach-Tarski construction requires the full power of the Axiom of Choice and non-measurable sets.
📌 Summary of Contributions
✅ Explained the mathematical structure of the Banach–Tarski paradox.
✅ Explored how free groups and orbit decompositions work in this context.
✅ Examined a finite approximation that helps build intuition about orbit behavior.
🧬 Real-Life Analogies (Expanded)
🧱 Infinite Lego Analogy
Imagine you have Lego bricks that can snap in infinitely many orientations. If you're allowed to rearrange infinitely many bricks using just rotations (not duplication or stretching), you can use a logic similar to Banach–Tarski.
🧪 Gas Molecule Rearrangement
Let’s say you have a perfectly isolated chamber of gas molecules. The molecules are countless and randomly moving. If somehow, you could identify orbits of individual molecules under transformation rules (e.g., time-evolving rotations) and assign symbolic colourings to each orbit, then, with a rule-based rotation function, you could rearrange subsets of the molecules such that the resulting distributions mimic two chambers.
Although this isn't physically possible due to quantum and atomic limitations, the conceptual framework allows you to think about entropy, molecule symmetries, and even quantum field models differently.
It builds a bridge between:
Thermodynamics (molecular states)
Symbolic mathematics (orbit-based partitions)
Information theory (entropy manipulation)
⚠️ Important Clarifications to Add
Why This Cannot Be Done Physically
Real objects are made of atoms (finite, measurable components)
The Axiom of Choice cannot operate on physical matter
Non-measurable sets have no physical meaning
The construction is purely mathematical, not implementable
What Makes This a "Paradox"
It contradicts our intuition about volume and space
It reveals deep issues with naive concepts of "measure"
It shows the power and strangeness of infinite mathematics
It's not actually contradictory - just counterintuitive
🧠 Deeper Real-World Applications
| Measure Theory | Demonstrates limitations of naive volume concepts |
| Group Theory | Shows power of free groups in geometry |
| Logic | Illustrates the consequences of the Axiom of Choice |
| Topology | Relates to problems in geometric topology |
| Education | Excellent example of counterintuitive mathematics |
📚 Historical Timeline
Timeline:
1924: Banach and Tarski prove the theorem
1985: Wagon's accessible book brings it to a wider audience
1990s: Various generalisations and related results
2000s: Connections to amenable groups explored
Present: Ongoing research in geometric group theory
📾 Final Thoughts
This paradox challenges our intuition about volume and duplication. By studying its mathematical structure through orbit decompositions and group actions, we gain insight into: The role of non-measurable sets in mathematics How the Axiom of Choice enables counterintuitive constructions The difference between mathematical possibility and physical reality The finite approximation discussed here helps build intuition, though the actual paradox requires the full machinery of advanced set theory and measure theory.
📚 References
Banach, S., & Tarski, A. (1924). Sur la décomposition des ensembles de points en parties respectivement congruentes.
Wagon, S. (1993). The Banach–Tarski Paradox. Cambridge University Press.
Dougherty, R., & Foreman, M. (1994). Banach–Tarski decompositions using sets with the property of Baire. Journal of the American Mathematical Society.
Tao, T. (Blog). Measure theory insights: https://terrytao.wordpress.com
Visual sources: Wikipedia Commons, Quanta Magazine, YouTube.
Educational exposition and visualisation approaches: Author's interpretation of standard material.
How a mathematical paradox allows infinite cloning. (2021, August 26). Quanta Magazine. https://www.quantamagazine.org/how-a-mathematical-paradox-allows-infinite-cloning-20210826/
🖋️ Written and developed by Abhinav Singh
Mechanical Engineering, IIT Gandhinagar
Summer of Math Exposition 2025
Subscribe to my newsletter
Read articles from Abhinav Singh Yadav directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
