Learn the Sliding Window Technique: A Simple Way to Solve Coding Problems 🚀
 AlgoAvengers 🚀
AlgoAvengers 🚀Introduction: Crack Coding Puzzles Fast! 🕵️♂️
Ever feel stuck checking every part of a list or word to solve a coding puzzle? The Sliding Window Technique, a powerful Data Structures and Algorithms (DSA) strategy, is like a detective’s magnifying glass, zooming in on just the right chunk of data to solve problems fast! It slides a “window” over arrays or strings, making your code efficient for coding interviews or competitions. Unlike the Two-Pointer technique, where pointers move freely to find pairs, Sliding Window focuses on a continuous chunk sliding left to right, like finding the best group of items (e.g., longest substring with no repeating letters). In DSA, this technique optimizes time and space, turning slow, repetitive solutions into sleek, linear ones!
Real-Life Analogy: Biking to Spot Four Unique Houses 🚴
Imagine you’re biking down a street, trying to find four consecutive houses with unique designs or colors (e.g., no two houses with the same style) for a CS project on pattern analysis. With the Sliding Window approach, you focus on a group of four houses in your view as you pedal. If the four houses don’t all have unique designs, you move forward one house, losing the oldest house from your view, and check the new group of four. For some tasks, you shrink your view to fewer than four houses to find a group with all unique designs, then try to expand it again. This saves time by avoiding redundant checks, a core DSA principle for efficient data processing!
Brute Force Approach (The Slow Way): Without Sliding Window, you’d stop at every house, check every possible group of four consecutive houses starting from there, and verify their designs. For a street with 100 houses, you’d check groups starting at house 1 (houses 1-4), house 2 (houses 2-5), and so on, up to house 97 (houses 97-100). This means recalculating designs for overlapping houses multiple times, leading to a lot of repeated work—slow and inefficient, like a brute force algorithm in DSA with O(n²) time complexity!
Why Sliding Window Wins: In DSA, Sliding Window reduces this repetition by sliding a focused “window” (like your bike’s view), processing each house at most twice (once entering, once leaving), achieving O(n) time. It’s like using a smart algorithm to optimize your pattern analysis project!
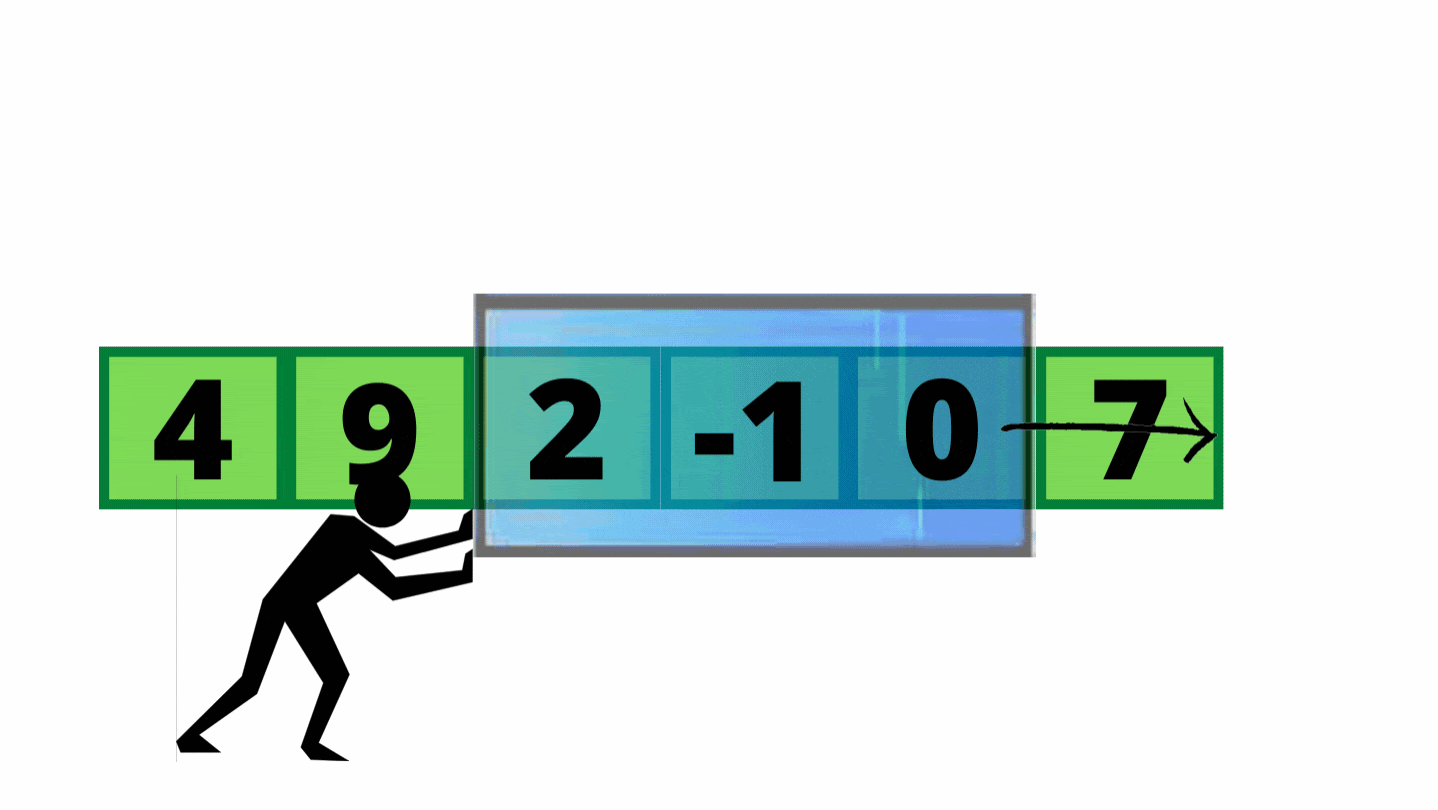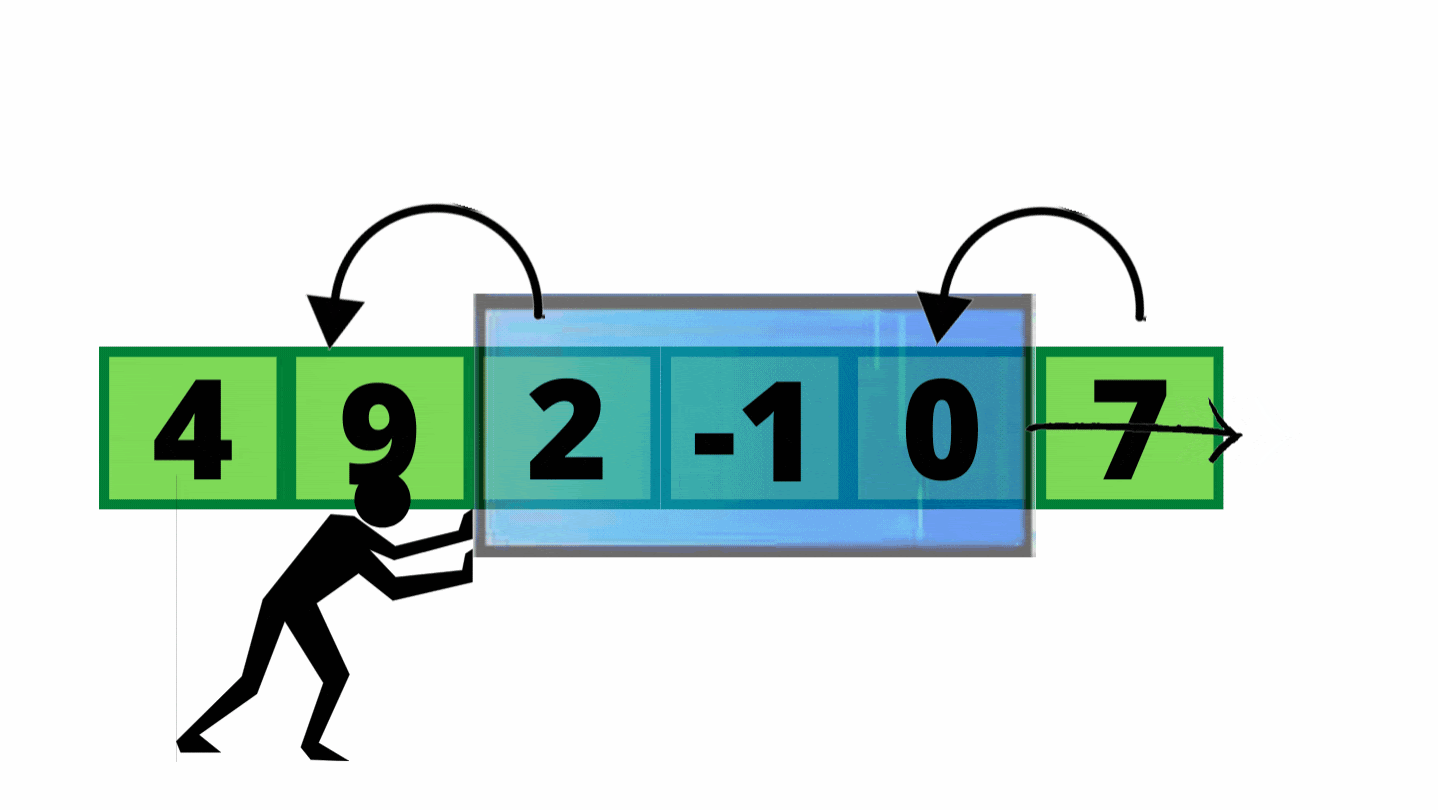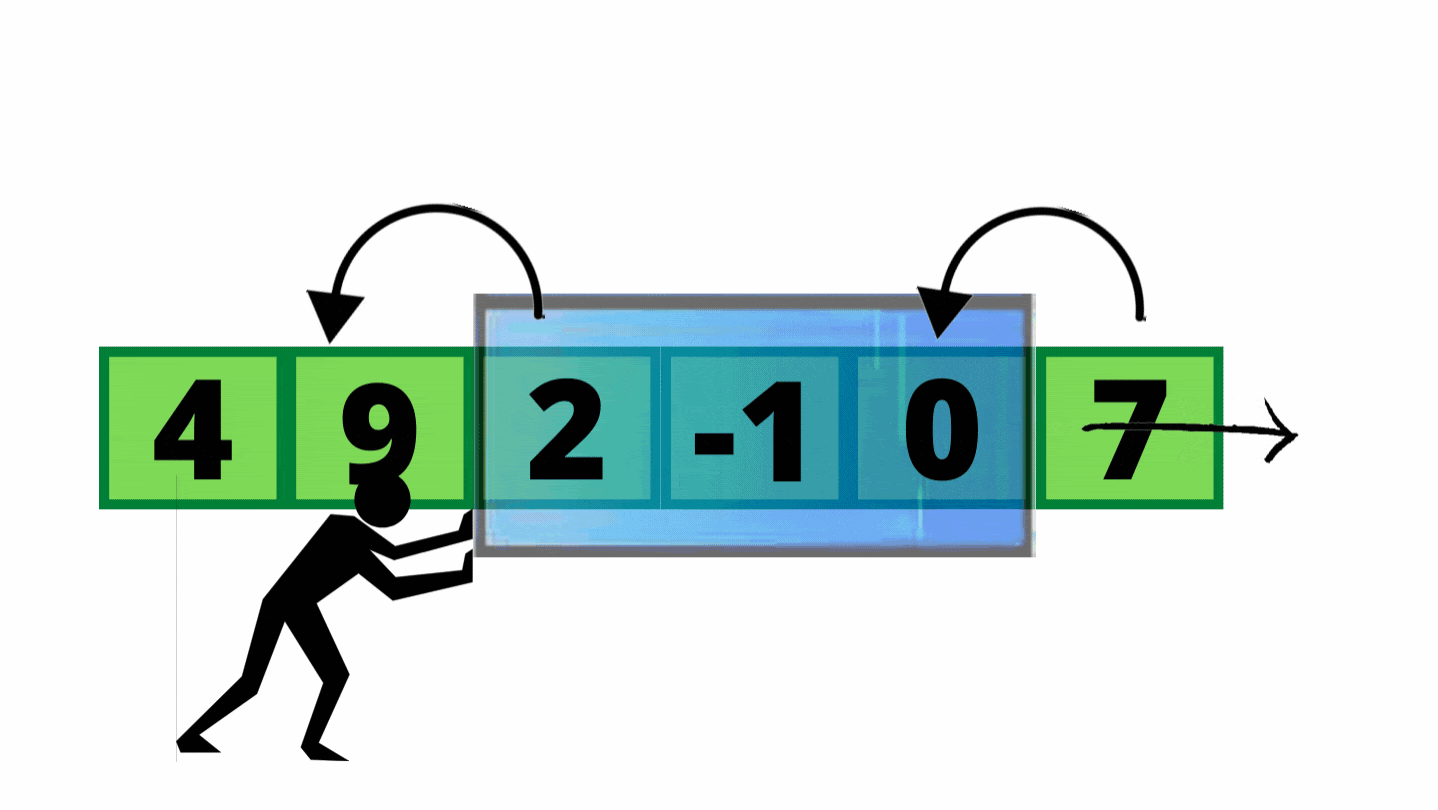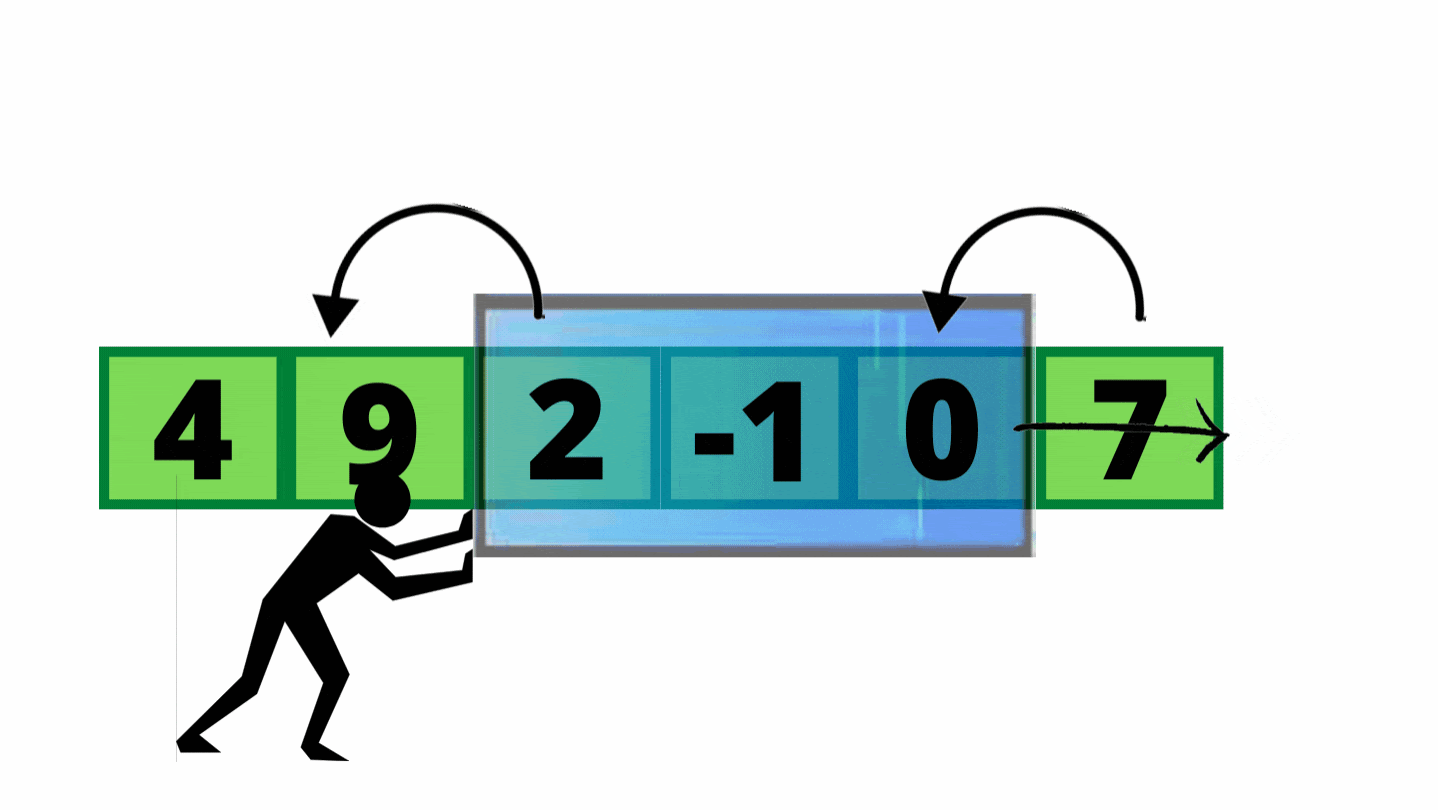
Why Use the Sliding Window? Why It’s Awesome! 🎯
Sliding Window is a DSA superstar because it skips redundant work, making your code:
Super Fast: Cuts slow O(n²) solutions to linear O(n) time, processing each item once.
Saves Effort: Only checks the new item entering and old item leaving the window, avoiding recalculations.
Memory Efficient: Uses minimal extra space (O(1) or O(k)), like a small hash map or variables.
What Can It Solve?
Sums or averages of a subarray.
Longest or shortest substring with a rule (like “no repeating letters”).
Checking for anagrams in a string.
Best subarray fitting a condition (like a sum less than a number).
When to Use the Sliding Window Technique 🔍
Use it for continuous chunks of arrays or strings (subarrays or substrings) in DSA problems. Examples:
Max/Min Problems: Biggest or smallest sum of a fixed-size group.
- Example: “Biggest sum of 4 numbers in a row.”
Special Groups: Chunks with a rule, like no more than 2 different letters.
- Example: “Longest substring with no repeating letters.”
Matching Patterns: Checking if a string has another string’s letters in any order.
- Example: “Does this string have a jumbled ‘cat’?”
Flexible Windows: Best chunk where size changes by a rule.
- Example: “Shortest subarray adding to 10.”
How to Think About Sliding Window: A Simple Plan 🧠
Here’s a DSA-inspired plan to apply Sliding Window:
Set Window Size: Decide if the window is fixed (e.g., 4 items) or variable (changes by rules).
Start the Window: Use
leftandrightpointers at the array/string’s start.Grow and Process: Move
rightto add items, calculating sums or counts.Shrink if Needed: If the window breaks the rule (e.g., sum too big), move
leftto shrink.Update Answer: Track the best result (e.g., longest window).
Slide Until Done: Repeat until
rightreaches the end.Return Result: Share the final answer, like the maximum sum or length.
Tools You’ll Use 🛠️
You’ll need these DSA tools:
Two Pointers:
leftandrightto mark window edges.Hash Maps or Arrays: To count items fast (e.g., letter frequencies in a string).
Sums or Counts: To track totals, like a sum or number of items.
Types of Sliding Window Problems with Easy Examples
Here’s how to tackle both types with code and examples, showing DSA efficiency.
1. Fixed Window Size 📏
The window stays the same size (e.g., 4 items). Slide it by moving both pointers.
Code Template:
void fixedWindow(vector<int>& list, int k) {
int left = 0;
int currentSum = 0;
// Sum first k items
for (int right = 0; right < k; right++) {
currentSum += list[right];
}
cout << currentSum << endl; // Show first window’s sum
// Slide the window
for (int right = k; right < list.size(); right++) {
currentSum += list[right]; // Add new item
currentSum -= list[left]; // Remove old item
left++; // Move left pointer
cout << currentSum << endl; // Show current window’s sum
}
}
Example: Maximum Sum of a Fixed Window
Find the maximum sum of any group of k numbers in a row.
#include <iostream>
#include <vector>
#include <algorithm> // For max
int maxWindowSum(vector<int>& numbers, int k) {
int left = 0;
long long currentSum = 0;
long long maxSum = 0;
// Sum first k numbers
for (int i = 0; i < k; i++) {
currentSum += numbers[i];
}
maxSum = currentSum;
// Slide the window
for (int right = k; right < numbers.size(); right++) {
currentSum += numbers[right]; // Add new number
currentSum -= numbers[left]; // Remove old number
left++; // Move left pointer
maxSum = max(maxSum, currentSum); // Update max sum
}
return maxSum;
}
int main() {
int n, k;
cout << "Enter list size and window size: ";
cin >> n >> k;
vector<int> numbers(n);
cout << "Enter numbers: ";
for (int i = 0; i < n; i++) {
cin >> numbers[i];
}
cout << "Maximum window sum: " << maxWindowSum(numbers, k) << endl;
return 0;
}
How It Works: Sum the first k numbers, slide by adding the next number and removing the oldest, tracking the maximum sum.
Time and Space Complexity:
Time Complexity (O(n)): We process each number once. For a list of size
n, we sum the firstknumbers (k steps), then slide acrossn-knumbers, adding and subtracting one number per slide. Total steps: roughlyn, so O(n) time. In DSA, this beats the brute force approach (like checking every group ofkhouses), which takes O(n²) time due to repeated calculations.Space Complexity (O(1)): We only use a few variables (
currentSum,maxSum,left), which don’t grow with input size. It’s like jotting down a single number in your bike’s notebook!Visual Analogy: It’s like biking past houses, keeping your view fixed on four houses, noting their combined value, instead of stopping to check every group of four houses (the O(n²) brute force way).
2. Variable Window Size 🔄
The window size changes by a rule. Grow until the rule breaks, then shrink.
Code Template:
void variableWindow(vector<int>& list) {
int left = 0;
int maxLength = 0;
// Add variables like hash map or sum
for (int right = 0; right < list.size(); right++) {
// Add item at 'right'
// Example: Add to sum or count letters
// Shrink if rule breaks
while (/* window breaks rule */) {
// Remove item at 'left'
left++; // Shrink window
}
// Update answer
maxLength = max(maxLength, right - left + 1);
}
// Use final answer
}
Example: Longest Word Without Repeating Letters
Find the longest substring with no repeating letters.
#include <string>
#include <map>
#include <algorithm> // For max
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int left = 0;
int maxLength = 0;
map<char, int> letters; // Count letters
for (int right = 0; right < s.size(); right++) {
char currentLetter = s[right];
letters[currentLetter]++; // Add new letter
// If letter repeats
while (letters[currentLetter] > 1) {
char leftLetter = s[left];
letters[leftLetter]--; // Remove leftmost letter
left++; // Shrink window
}
// Update longest length
maxLength = max(maxLength, right - left + 1);
}
return maxLength;
}
};
How It Works: Add letters until one repeats, shrink by removing letters from the left, and track the longest window.
Time and Space Complexity:
Time Complexity (O(n)): Each character is processed at most twice—once when added (via
right) and once when removed (vialeftwhen shrinking). For a string of lengthn, this means O(n) time. In DSA, this is much faster than the brute force approach (like checking every substring for duplicates), which takes O(n²) or more.Space Complexity (O(k)): We use a hash map to track letter counts, with size depending on the number of unique characters (e.g., 26 for lowercase letters), so O(k) space, where
kis the character set size. It’s like keeping a small checklist of house designs in your bike’s notebook!Visual Analogy: It’s like biking past houses, adjusting your view to include only houses with unique designs, tracking them in a small note, instead of checking every house combination (the O(n²) brute force way).
Fixed vs. Variable Window: A Quick Comparison 📊
Sliding Window problems are either Fixed Window (same size) or Variable Window (size changes). Here’s how they differ in DSA:
| Feature | Fixed Window | Variable Window |
| Window Size | Always the same (e.g., 4 items). | Changes based on a rule (e.g., no repeats). |
| How It Moves | Both pointers move together to keep size fixed. | right grows, left shrinks if rule breaks. |
| Example Problem | Maximum sum of k numbers. | Longest substring with no repeating letters. |
| When to Use | When size is fixed. | When size depends on conditions. |
| Code Complexity | Simpler, fixed size. | Trickier, dynamic size. |
Visual Example: Fixed Window is a bicycle view always covering 4 houses. Variable Window shrinks or grows to include houses with unique designs.
Practice Problems to Try! 🏋️
Try these beginner-friendly LeetCode problems to apply Sliding Window in DSA:
Fixed Window Size:
Maximum Average Subarray I – Highest average of a fixed group.
Find All Anagrams in a String – Find jumbled versions of a word.
Maximum Number of Vowels in a Substring of Given Length – Count vowels in a fixed window.
Variable Window Size:
Longest Substring Without Repeating Characters – Longest substring with no repeating letters.
Minimum Size Subarray Sum – Shortest subarray adding to a target.
Fruit Into Baskets – Collect fruits with a type limit.
Conclusion: Slide to Coding Success with DSA! 🎉
The Sliding Window technique is a DSA game-changer for solving coding problems fast. By sliding a window over your data, like biking past houses, you skip redundant work, achieving O(n) time and often O(1) or O(k) space, unlike the slow O(n²) brute force approach. Practice these problems, and you’ll master this essential DSA technique like a pro!
🔗 Stay Connected!
Want more DSA tips? Join our AlgoAvengers community:
💼 LinkedIn: https://www.linkedin.com/company/algo-avengers/
📢 Telegram: https://t.me/Free_Courses_N_Internships
🚀 Join thousands of learners leveling up their coding skills!
Thanks for Reading! 🙌
I hope you enjoyed learning about the Sliding Window Technique! Share your favorite Sliding Window problem below, and join our AlgoAvengers community to keep exploring DSA together. Happy coding!
Author: Amit kumar Meena
Subscribe to my newsletter
Read articles from AlgoAvengers 🚀 directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

AlgoAvengers 🚀
AlgoAvengers 🚀
AlgoAvengers is a dev-first platform delivering curated tech news, career tips, and job updates — daily. We post theme-based blogs 7 days a week, covering: 💡 Dev concepts 🧠 Career & motivation 🔧 Tools & resources 📰 Weekly tech news (#FinalCommit) Join 8k+ developers growing with clarity, not chaos. 🚀