Mastering the Fast and Slow Pointer Pattern: The Hare & Tortoise of DSA 🐢🐇
 AlgoAvengers 🚀
AlgoAvengers 🚀🚀 Introduction: The Hidden Power in Pacing
In the world of Data Structures and Algorithms (DSA), the Fast and Slow Pointer pattern, also known as the Tortoise and Hare algorithm, is a brilliant strategy for solving problems related to cycles, midpoints, and palindromes—especially in linked lists and arrays.
This pattern uses two pointers that move through a data structure at different speeds. With O(n) time and O(1) space, it can detect cycles, find the middle element, or even check if a structure is a palindrome. It’s like watching a tortoise and a hare race around a track—except here, it helps you crack coding puzzles fast and efficiently!
🏁 Real-Life Analogy: The Race Track With Loops
Imagine a circular race track. A tortoise moves one step at a time, while a hare sprints ahead two steps at a time. If the track has a loop, the faster hare will eventually catch up and overlap the tortoise. But if it’s a straight path, the hare will simply run off the track. That’s the essence of this approach—loop detection and position tracking by varying speeds!
💼 Real-World Applications
Here are real scenarios where the Fast and Slow Pointer approach shines:
🔁 Symlink Verification
In large file systems, symbolic links (symlinks) might point to other files or even each other. Sometimes a symlink forms a loop (A → B → A). Using two pointers that follow links at different speeds helps detect such infinite loops efficiently.
🔄 Object-Oriented Compilation
During compilation, a class might depend on another which indirectly depends back on the first (circular dependency). This pattern helps identify such cyclic dependencies in module graphs.
⚙️ Behind the Magic: How It Works
Let’s say:
m= distance from head to start of loopk= distance from loop start to the meeting pointn= length of the loop
When fast and slow pointers meet:
Distance by slow = m + n*y + k
Distance by fast = m + n*x + k
Since fast is 2x the speed:
m + n*x + k = 2(m + n*y + k)
⇒ m + k = (x - 2y)n ⇒ m + k is multiple of n
This means that after the meeting, if we reset the slow pointer to the head, and move both one step at a time, they’ll meet at the start of the cycle after m steps. That’s your loop start!
🎯 Does Your Problem Match This Pattern?
Use this pattern if:
✅ You’re working with a linear structure like:
Linked Lists
Arrays
Strings
And one of the following applies:
🔁 You need to detect a cycle
📍 You want to find the midpoint or second quantile
📌 You’re checking for intersections between two structures
🧰 Fast and Slow Pointers: Code Template
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
// condition met
}
}
🧪 Problem Examples with Naive vs Optimized Approaches
1️⃣ Detect Cycle in a Linked List
Check whether a singly linked list contains a loop (cycle). A cycle occurs when a node’s next pointer refers back to one of the previous nodes.
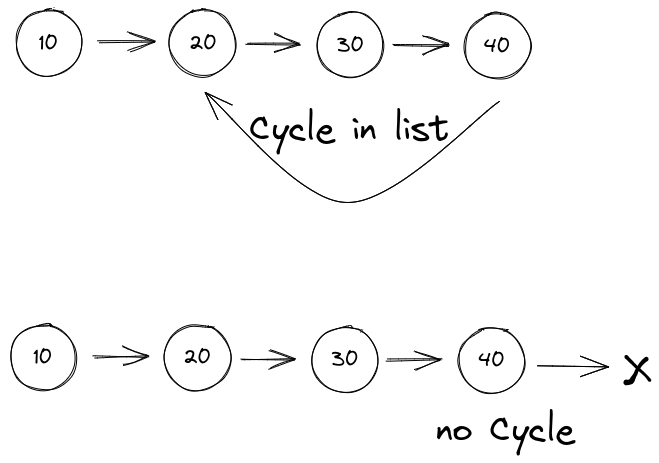
🐢 Naive Approach (using a HashSet):
bool hasCycle(ListNode* head) {
unordered_set<ListNode*> visited;
while (head) {
if (visited.count(head)) return true;
visited.insert(head);
head = head->next;
}
return false;
}
⛔ Time: O(n), Space: O(n)
🐇 Optimized Fast and Slow Pointer:
bool hasCycle(ListNode* head) {
ListNode* slow = head;
ListNode* fast = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) return true;
}
return false;
}
✅ Time: O(n), Space: O(1)
🎉 Benefits:
No extra memory
Elegant and efficient
Ideal for large linked lists
2️⃣ Find the Middle of a Linked List
Given the head of a singly linked list, find its middle node. If the list has even nodes, return the second middle.

ListNode* findMiddle(ListNode* head) {
ListNode* slow = head;
ListNode* fast = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
return slow;
}
As fast moves two steps while slow moves one, when fast reaches the end, slow is halfway through. That’s your middle node—found in just one pass!
3️⃣ Check if a Linked List is a Palindrome
Check whether a singly linked list is a palindrome (same forwards and backwards).
bool isPalindrome(ListNode* head) {
ListNode* slow = head;
ListNode* fast = head;
// Step 1: Find middle
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
// Step 2: Reverse second half
ListNode* prev = nullptr;
while (slow) {
ListNode* temp = slow->next;
slow->next = prev;
prev = slow;
slow = temp;
}
// Step 3: Compare both halves
ListNode* left = head;
ListNode* right = prev;
while (right) {
if (left->val != right->val) return false;
left = left->next;
right = right->next;
}
return true;
}
First, use fast and slow pointers to reach the middle. Then reverse the second half of the list and compare node by node with the first half. If all values match, it’s a palindrome!
🧠 Strategy Time: When to Apply This Pattern
| Problem Type | Use Fast & Slow? |
| Loop Detection in Linked Lists | ✅ Yes |
| Midpoint of a Linked List | ✅ Yes |
| Palindrome Check | ✅ Yes |
| Subarray/Substring Problems | ❌ Use Sliding Window instead |
| Tree Problems | ❌ Other techniques preferred |
🏋️ Practice Problems to Try
| Problem | Platform |
| Linked List Cycle | LeetCode |
| Palindrome Linked List | LeetCode |
| Middle of the Linked List | LeetCode |
| Circular Array Loop | LeetCode |
🎉 Conclusion: Elegant Logic, Powerful Results
The Fast and Slow Pointer technique is your go-to pattern for problems involving cycle detection, midpoint finding, or palindrome verification—especially in linked lists. With its O(n) time and O(1) space complexity, it provides efficient, elegant solutions without unnecessary memory usage.
Add this tool to your DSA toolbox, and race ahead in your problem-solving journey!
🔗 Stay Connected!
💼 LinkedIn: AlgoAvengers
📢 Telegram Community
✍️ Author: Amit kumar Meena
Thanks for reading 📖
Subscribe to my newsletter
Read articles from AlgoAvengers 🚀 directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

AlgoAvengers 🚀
AlgoAvengers 🚀
AlgoAvengers is a dev-first platform delivering curated tech news, career tips, and job updates — daily. We post theme-based blogs 7 days a week, covering: 💡 Dev concepts 🧠 Career & motivation 🔧 Tools & resources 📰 Weekly tech news (#FinalCommit) Join 8k+ developers growing with clarity, not chaos. 🚀