🚀 Cyclic Sort: The Ultimate A-Z Guide
 AlgoAvengers 🚀
AlgoAvengers 🚀🎯 Introduction: Why Master Cyclic Sort?
You’re in a DSA interview…
"Given an array of numbers in a known range (like 1 to n), find what’s missing or duplicated?"
"How would you sort the array in-place, O(n) time, O(1) space?"
Hash tables and brute force work, but DSA champions think Cyclic Sort.
It’s your Swiss Army knife for finding missing/duplicate numbers or sorting in-range arrays—blazing fast and memory-cheap.
This is your A–Z Cyclic Sort resource: analogies, dry runs, C++ code, pitfalls, problem links, and real-world applications. Buckle up!
🍽️ The Dining Table Analogy: Cyclic Sort Made Visual
Imagine a round table with seats numbered 1 to n.
Guests show up with their "assigned seat" number, but everybody sits randomly.

The solution?
➡️ Each guest checks their card: ⮑ If not at their seat, swaps with whoever is in their spot— ⮑ Repeat until everyone lands home.
That’s exactly what Cyclic Sort does to an array!
🛑 When Should You Use Cyclic Sort? (Pattern Recognition)
Use Cyclic Sort when:
The array contains numbers within a consecutive range (e.g., 1–n, 0–n).
Problems ask to: “Find missing/duplicate/corrupt” elements within that range.
O(n) time and O(1) space constraints are given; in-place modification is allowed.
You need to sort such an array in-place, check IDs, or scan range data for errors.
Important: Cyclic Sort is not for arbitrary or out-of-range arrays—you need that consecutive numeric guarantee!
🛠️ The Cyclic Sort Pattern: Visuals, Walkthroughs & Pseudocode
Step-by-Step Logic
Put Each Element in its “Seat”:
Scan the array left-to-right, starting from index
i = 0.If
nums[i]is not at its correct sorted position (which for a 1-to-n range isnums[i]-1), swapnums[i]with the element currently atnums[i]-1.Advance
ito the next element only when:nums[i]is already at its correct place.nums[i]is out-of-range (e.g., negative or greater than n).nums[i]is a duplicate of the value already atnums[i]-1, preventing an infinite loop.
One Pass: Detect Missing and Duplicates (After the first pass is complete):
Iterate through the array again. For each index
i:- If
nums[i] != i + 1, theni+1is a missing number, andnums[i]is likely a duplicate or misfiled.
- If
💻 Universal Pseudocode
i = 0
while i < n:
correct_index = nums[i] - 1 # For 1-to-n range
if nums[i] > 0 and nums[i] <= n and nums[i] != nums[correct_index]:
swap(nums, i, correct_index)
else:
i += 1
# Now traverse to check for mismatches (e.g., find missing or duplicates)
for i from 0 to n-1:
if nums[i] != i+1:
# i+1 is missing, nums[i] is a duplicate (or an out-of-place element)
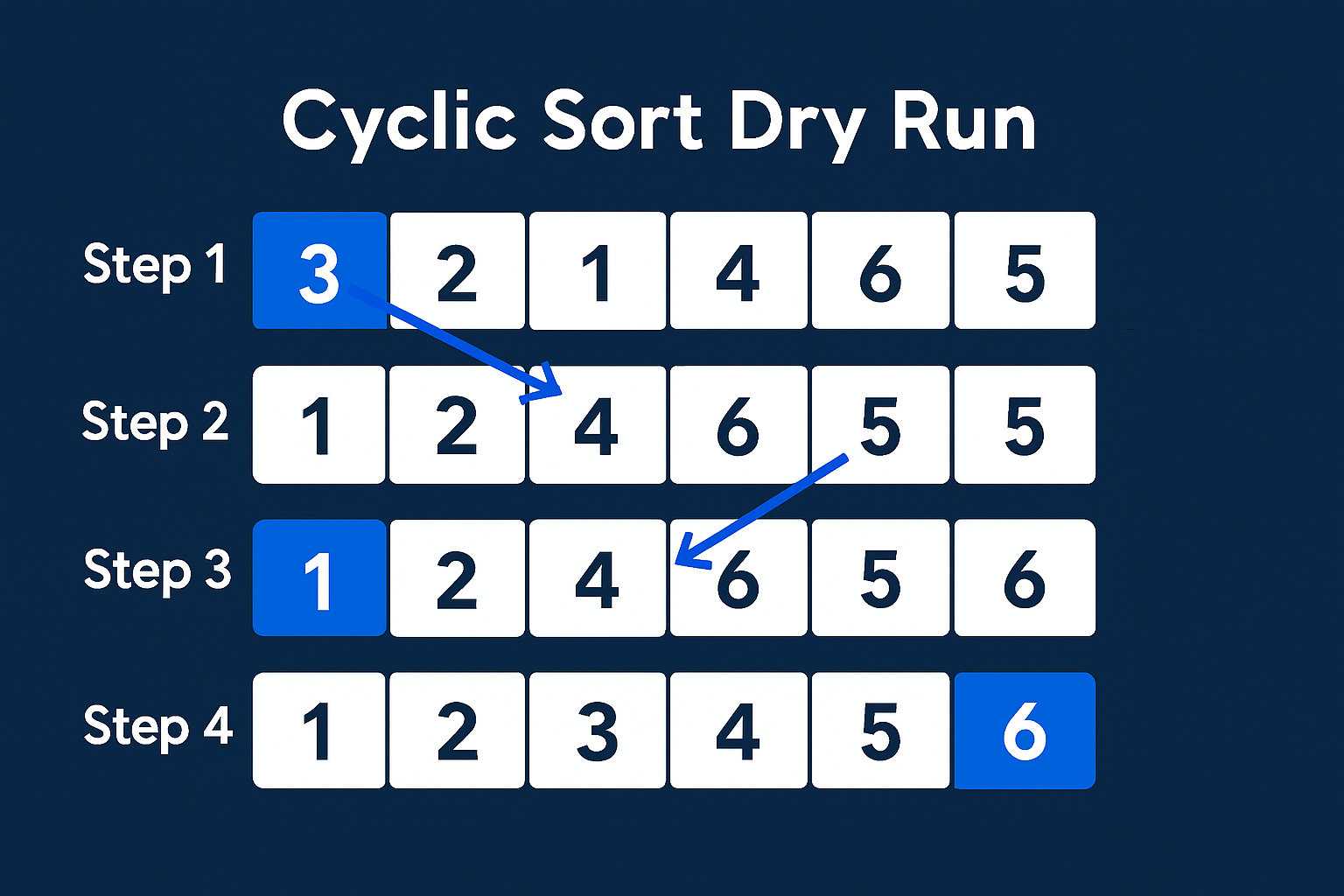
👀 Visual Flow: Dry Run Example
Let's trace nums = [3, 2, 1, 4, 6, 5] as it gets sorted cyclically. Pay close attention to how elements move towards their correct "seat."
Explanation of the Visual:
Starting with 3 at index 0: The number 3 belongs at index 2 (since 3−1=2). It swaps with the number currently at index 2, which is 1. The array becomes
[1, 2, 3, 4, 6, 5]. Now 1 is at index 0.Next, 1 at index 0: The number 1 belongs at index 0 (since 1−1=0). It's already in its correct spot. We move to the next index.
Next, 6 at index 4: The number 6 belongs at index 5. It swaps with the number currently at index 5, which is 5. The array becomes
[1, 2, 3, 4, 5, 6]. Now 5 is at index 4.Next, 5 at index 4: The number 5 belongs at index 4. It's already in its correct spot. We move to the next index.
The process continues until all elements are in their correct positions, completing the cycles.
🔬 Behind the Scenes: What Makes Cyclic Sort “Cyclic”?
Swapping Follows “Hidden Cycles”: Every misplaced element initiates a cycle of swaps. For example, if '3' is at index '0' and '1' is at index '2', '3' wants to go to index '2', displacing '1', which wants to go to index '0'. This forms a cycle (0 -> 2 -> 0). Swapping eventually brings all elements within that cycle to their correct places. This ensures efficiency.
No Redundant Work: Each value only moves when it directly improves the state of the array, bringing it closer to its sorted form. Once an element is placed in its correct position, it is never touched again.
Pitfall-Prone Cases (and How to Avoid Them):
| Condition | Impact |
nums[i] > 0 && nums[i] <= nums.size() | Shields against out-of-bounds swaps when numbers are negative or too large. |
nums[i] != nums[correct_index] | Crucial! Prevents infinite swaps when duplicate elements are present. |
- Minimal Moves, Guaranteed O(n): Cyclic Sort’s "internal engine" ensures that each misplaced value gets exactly one "ride home" (i.e., it participates in at most one chain of swaps that leads it to its final position). This guarantees that the algorithm performs at most O(n) swaps, leading to an overall O(n) time complexity with O(1) extra space, making it highly efficient.
🧑💻 C++ Implementation
void cyclicSort(vector<int>& nums) {
int i = 0;
while (i < nums.size()) {
int correct = nums[i] - 1; // Calculate correct index for nums[i] (assuming 1-based range)
// Condition 1: Check if nums[i] is within the valid range (1 to N)
// Condition 2: Check if nums[i] is NOT already at its correct place
// If both are true, perform the swap
if (nums[i] > 0 && nums[i] <= nums.size() && nums[i] != nums[correct]) {
swap(nums[i], nums[correct]);
} else {
// If nums[i] is already in its correct place, or out of range, or
// it's a duplicate of the element already at its correct_index,
// then move to the next element.
++i;
}
}
}
🏭 Real-World Applications of Cyclic Sort
Cyclic Sort isn't just for interviews; it has powerful applications in various domains:
| Domain | Use Case |
| Databases | Ensure all IDs (students, employees, barcodes) are present and unique. |
| Tickets/Events | Detect/repair double-booked or empty seats in allocation systems. |
| IoT/Sensor Data | Spot missing or duplicate readings by sequence numbers in data streams. |
| Genomics/Analytics | Catch missing gene or survey codes in large datasets. |
🔥 Brute Force vs. Cyclic Sort (with C++ Templates)
Let's compare common problem-solving approaches to highlight Cyclic Sort's superiority.
1️⃣ Find All Missing Numbers [1, n]
Problem: Given an array nums of n integers where nums[i] is in the range [1,n] and each integer appears once or twice, return an array of all the integers in the range [1,n] that do not appear in nums.
💩 Brute Force (Hash Set: O(n) time & O(n) space)
This approach uses a hash set to keep track of present numbers.
vector<int> findDisappearedNumbers(vector<int>& nums) {
unordered_set<int> present(nums.begin(), nums.end());
vector<int> missing;
for (int i = 1; i <= nums.size(); ++i)
if (!present.count(i)) // or present.find(i) == present.end()
missing.push_back(i);
return missing;
}
🚀 Cyclic Sort (Optimal: O(n) time, O(1) space!)
This is the optimal Cyclic Sort solution leveraging O(1) space.
vector<int> findDisappearedNumbers(vector<int>& nums) {
int i = 0;
while (i < nums.size()) {
int correct = nums[i] - 1; // Correct index for nums[i]
if (nums[i] != nums[correct]) { // If not in correct place AND not a duplicate already in correct place
swap(nums[i], nums[correct]);
} else {
++i; // Move forward if already in correct place or is a duplicate
}
}
vector<int> missing;
for (int i = 0; i < nums.size(); ++i) {
if (nums[i] != i + 1) { // If the number at index i is not what it should be (i+1), then i+1 is missing
missing.push_back(i + 1);
}
}
return missing;
}
2️⃣ Find the Missing Number [0, n]
Problem: Given an array nums containing n distinct numbers in the range [0,n], return the only number in the range that is missing from the array.
Math Formula (Only for 1 Missing: O(n) time, O(1) space)
A simple mathematical approach if only one number is missing.
int missingNumber(vector<int>& nums) {
int n = nums.size();
long long total = (long long)n * (n + 1) / 2; // Sum of numbers from 0 to n
long long sum = 0;
for (int a : nums) sum += a;
return total - sum; // The difference is the missing number
}
Cyclic Sort (General, Handles More: O(n) time, O(1) space)
Cyclic Sort offers a more generalized solution that can be adapted for scenarios beyond just one missing number.
int missingNumber(vector<int>& nums) {
int n = nums.size();
int i = 0;
while (i < n) {
// Correct position for nums[i] in a 0-to-n range is nums[i] itself,
// unless nums[i] is 'n' (which has no place in a 0 to n-1 indexed array)
if (nums[i] < n && nums[i] != nums[nums[i]]) {
swap(nums[i], nums[nums[i]]);
} else {
++i;
}
}
// After cyclic sort, the missing number is the first index that doesn't match its value
for (int i = 0; i < n; ++i) {
if (nums[i] != i) return i;
}
return n; // If all numbers from 0 to n-1 are present, then n is the missing number
}
3️⃣ Find the Duplicate Number
Problem: Given an array of integers nums containing n+1 integers where each integer is in the range [1,n] inclusive. There is only one repeated number in nums, return this repeated number.
💩 Naive Approaches (e.g., Sorting, Hash Map)
Sorting: Sort the array (O(NlogN) time, O(1) space if in-place sort like heapsort). Then, iterate to find adjacent duplicates.
// T.C.-O(N*logN), S.C.-O(1) int findDuplicate(vector<int>& nums) { sort(nums.begin(), nums.end()); for(int i = 0; i < nums.size() - 1; i++) { if(nums[i] == nums[i + 1]) { return nums[i]; } } return -1; // Problem guarantees a duplicate, so theoretically unreachable }Hash Map: Uses a hash map to count frequencies. O(N) time, but O(N) space.
// T.C.-O(N), S.C.-O(N) int findDuplicate(vector<int>& nums) { unordered_map<int, int> mp; for(int num : nums) mp[num]++; for(auto const& [key, val] : mp) { // Iterate map for duplicates if(val >= 2) { return key; } } return -1; // Problem guarantees a duplicate, so theoretically unreachable }
🚀 Cyclic Sort (Optimal: O(N) Time, O(1) Space
int findDuplicate(vector<int>& arr){
int n = arr.size();
int i = 0;
while (i < n) {
int correct_idx = arr[i] - 1; // Calculate correct index for current number (1-based to 0-based)
// If the current number is not at its correct position AND
// the value at its correct position is NOT already a duplicate of the current number
if (arr[i] != arr[correct_idx]) {
swap(arr[i], arr[correct_idx]);
} else {
// If arr[i] is already at its correct place, OR it's a duplicate
// that is now at its correct position (i.e., arr[i] == arr[correct_idx]),
// then we move to the next element.
i++;
}
}
// After cyclic sort, the duplicate will be the element that is NOT at its 'correct' spot (i+1)
// and is therefore a repeat of some other number.
for(int k = 0; k < n; k++) {
if(arr[k] != k + 1) {
return arr[k]; // This element is the duplicate
}
}
return -1; // Should not be reached based on problem constraints
}
4️⃣ Find All Duplicates in an Array
Problem: Given an integer array nums of length n where all the integers of nums are in the range [1,n] and each integer appears once or twice, return an array of all the integers that appear twice.
// Cyclic Sort: T.C. - O(N), S.C. - O(1)
vector<int> findDuplicates(vector<int>& nums) {
int n = nums.size();
int i = 0;
while(i < n) {
int correct = nums[i] - 1; // Correct index for nums[i]
if (nums[i] != nums[correct]) { // If not in correct place AND not a duplicate already in correct place
swap(nums[i], nums[correct]);
}
else {
i++; // Move forward if already in correct place or is a duplicate
}
}
vector<int> res;
// After cyclic sort, iterate to find elements that are not in their sorted position
for(int i = 0; i < n; i++) {
if(nums[i] != i + 1) {
res.push_back(nums[i]); // These are the duplicates
}
}
return res;
}
5️⃣ Find All Numbers Disappeared in an Array
Problem: Given an array nums of n integers where nums[i] is in the range [1,n] and each integer appears once or twice, return an array of all the integers in the range [1,n] that do not appear in nums.
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n = nums.size();
int i = 0;
// Cyclic sort . T.C.- O(N), S.C.- O(1).
while(i < n) {
int correct = nums[i] - 1; // Correct index for nums[i]
if(nums[i] != nums[correct]) { // If not in correct place AND not a duplicate already in correct place
swap(nums[i], nums[correct]);
} else {
i++; // Move forward if already in correct place or is a duplicate
}
}
vector<int> res;
for(int i = 0; i < n; i++) {
if(nums[i] != i + 1) { // If the number at index i is not what it should be (i+1), then i+1 is missing
res.push_back(i + 1);
}
}
return res;
}
📚 Must-Practice Problems & Further Skill Paths
To truly master Cyclic Sort and its variations, tackle these problems:
Level 0: Basics
- Sort 1–n array (GeeksforGeeks)
Level 1: Foundation
Level 2: Intermediate
Level 3+: Advanced
First K Missing Positives (GeeksforGeeks)
Shuffle String (LeetCode) - While not a pure Cyclic Sort, this problem often involves similar concepts of placing elements at their correct target indices.
🧭 Cyclic Sort—When & Not to Use: Cheat Sheet
| Scenario | Cyclic Sort? | Best Alternative | Notes |
| Sort 1–n in-place | ✅ | Classic Sorts | O(1) memory, stable for fixed ranges. |
| Find all missing numbers [1,n] | ✅ | Hash Set | O(1) space, perfect for huge arrays where memory is a concern. |
| Find duplicate(s) in [1, n] | ✅ | Count Array | Memory efficient for very large N. |
| Missing number [0, n] | ✅ | Math Formula | Cyclic more general for variants (e.g., multiple missing/duplicates). |
| Out-of-range/random keys | ❌ | Hash/Sort | Not suitable—requires a strict consecutive range guarantee. |
| First K missing positives | ✅ | Heap/Partial Sort | Cyclic can be cleverly adapted for this advanced scenario. |
Export to Sheets
😎 Pro Tips & Pitfalls
Check index bounds in swaps: Always ensure
nums[i]is within the valid range (1 to N or 0 to N−1) before calculatingcorrect_indexand performing a swap. This avoidsIndexOutOfBoundsExceptionorsegmentation fault.Never swap value with itself: The condition
nums[i] != nums[correct]is vital. Ifnums[i]is already in its correct spot, attempting to swap it with itself (or the element already there, which is itself) can lead to infinite loops, especially with duplicates.Only use for bounded range arrays: Cyclic Sort thrives on the property that numbers map directly to indices. It's not suitable for arbitrary keys or arrays with elements widely outside a consecutive range.
🏁 Conclusion: Cyclic Sort = DSA Power & Real-World Ready
Summary:
Cyclic Sort elegantly handles array problems involving numbers in a specific consecutive range.
It swaps elements to their rightful home, instantly detecting anomalies like missing numbers or duplicates.
It operates with no extra space (O(1)) and is blazing fast (O(n)), making it robust for real-world scenarios.
Memorize this powerful pattern for your next coding interview, data engineering side-projects, or whenever you want to impress with an optimal, efficient solution!
📢 Stay Connected with AlgoAvengers
Share your Cyclic Sort “AHA!” moment or toughest bug below. Ready for your next DSA quest? Let’s go!
Subscribe to my newsletter
Read articles from AlgoAvengers 🚀 directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

AlgoAvengers 🚀
AlgoAvengers 🚀
AlgoAvengers is a dev-first platform delivering curated tech news, career tips, and job updates — daily. We post theme-based blogs 7 days a week, covering: 💡 Dev concepts 🧠 Career & motivation 🔧 Tools & resources 📰 Weekly tech news (#FinalCommit) Join 8k+ developers growing with clarity, not chaos. 🚀