Binary Search Tree Iterator

Problem

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST): (link)

• BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.

• boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.

• int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

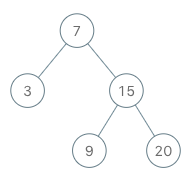
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

• The number of nodes in the tree is in the range [1, 10<sup>5</sup>].

• 0 <= Node.val <= 10<sup>6</sup>

• At most 10<sup>5</sup> calls will be made to hasNext, and next.

Follow up:

• Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

Solution

Idea: The iterator is essentially the in-order traversal list of the BST. We don't use any specific properties of the BST; it's simply the in-order traversal of the binary tree.

The simplest approach would be to store the in-order traversal in a list, but this would require O(n) space. To reduce the space complexity to O(h), where h is the height of the BST, we need to mimic the in-order traversal of the binary tree.

In-order traversal is straightforward: it goes as far left as possible from the root node, then visits the parent node, moves right, and again goes as far left as possible. This process continues. We store all the left nodes in a stack, and the maximum height of the stack will be O(h).

When we pop the top of the stack, it is the current next element in the BST. We then immediately move right and push all the left nodes from there. If the stack is empty, there is no next element.

Time - O(h)

Space - O(h)

class BSTIterator {
    private Deque<TreeNode> stack = new ArrayDeque<>();

    public BSTIterator(TreeNode root) {
        pushAllLeft(root);
    }

    public int next() {
        TreeNode nextNode = stack.pop();
        pushAllLeft(nextNode.right);
        return nextNode.val;
    }

    public boolean hasNext() {
        return !stack.isEmpty();
    }

    private void pushAllLeft(TreeNode node){
        while(node!=null){
            stack.push(node);
            node = node.left;
        }
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * int param_1 = obj.next();
 * boolean param_2 = obj.hasNext();
 */