Implementing Graphs in Golang Without Starting from Scratch

Have you ever imagined a world without connections? Think about your social media full of random unknown people in your follow recommendations, maps not showing the shortest direction between two destinations, or file imports turning into a mess of unrelated modules after compiling. This would be hard even to imagine, right?

This type of core data is managed by creating connections between it, thereby forming a network of relationships. In programming terms, we call this a graph data structure.

In this article, you'll see how to use this structure to solve any problems related to relations.

What is a Graph?

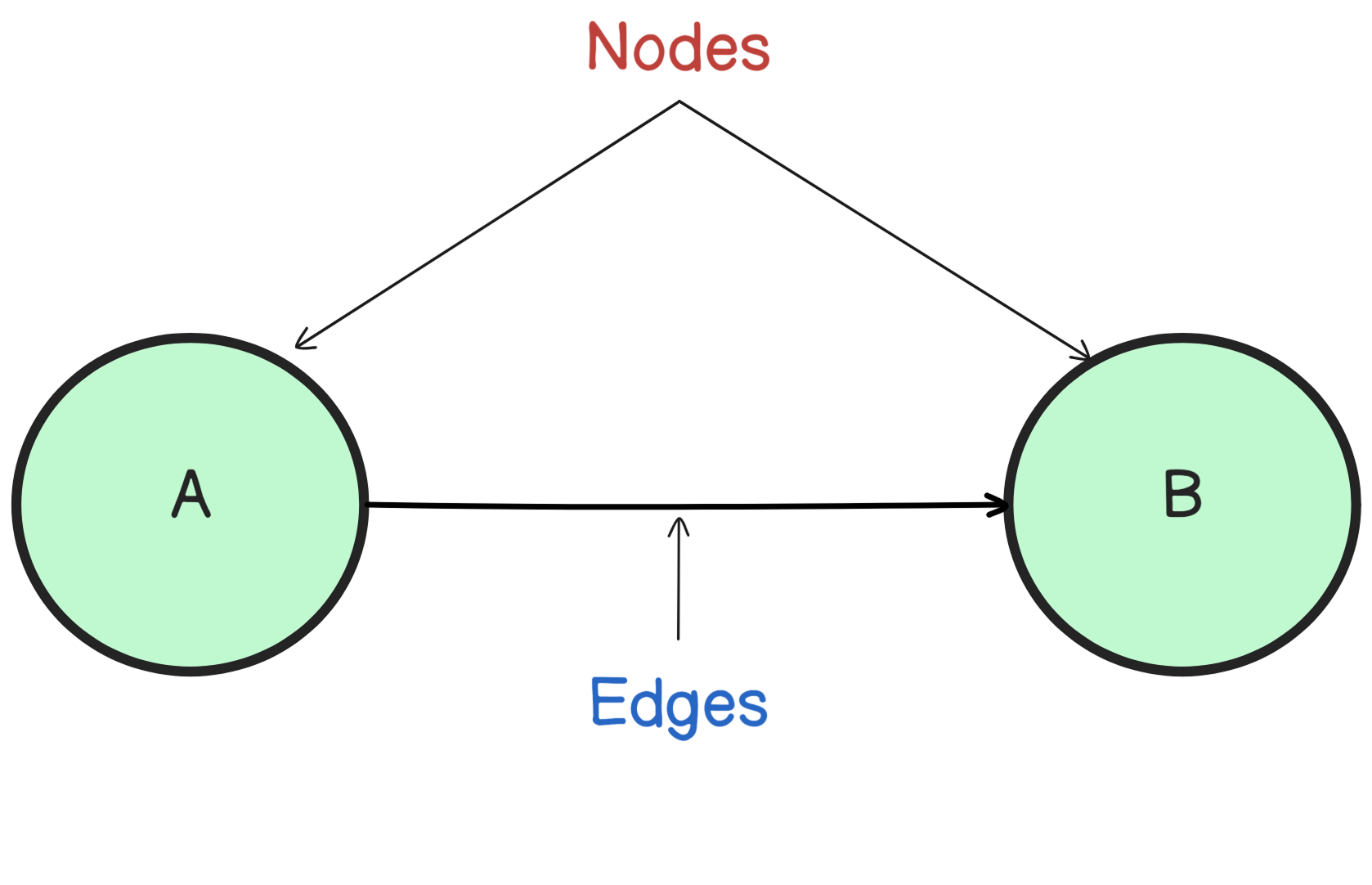
A graph is a nonlinear data structure that contains nodes and edges. A node (or vertex) is just a single unique value, while an edge represents a connection or relationship between two of these nodes.

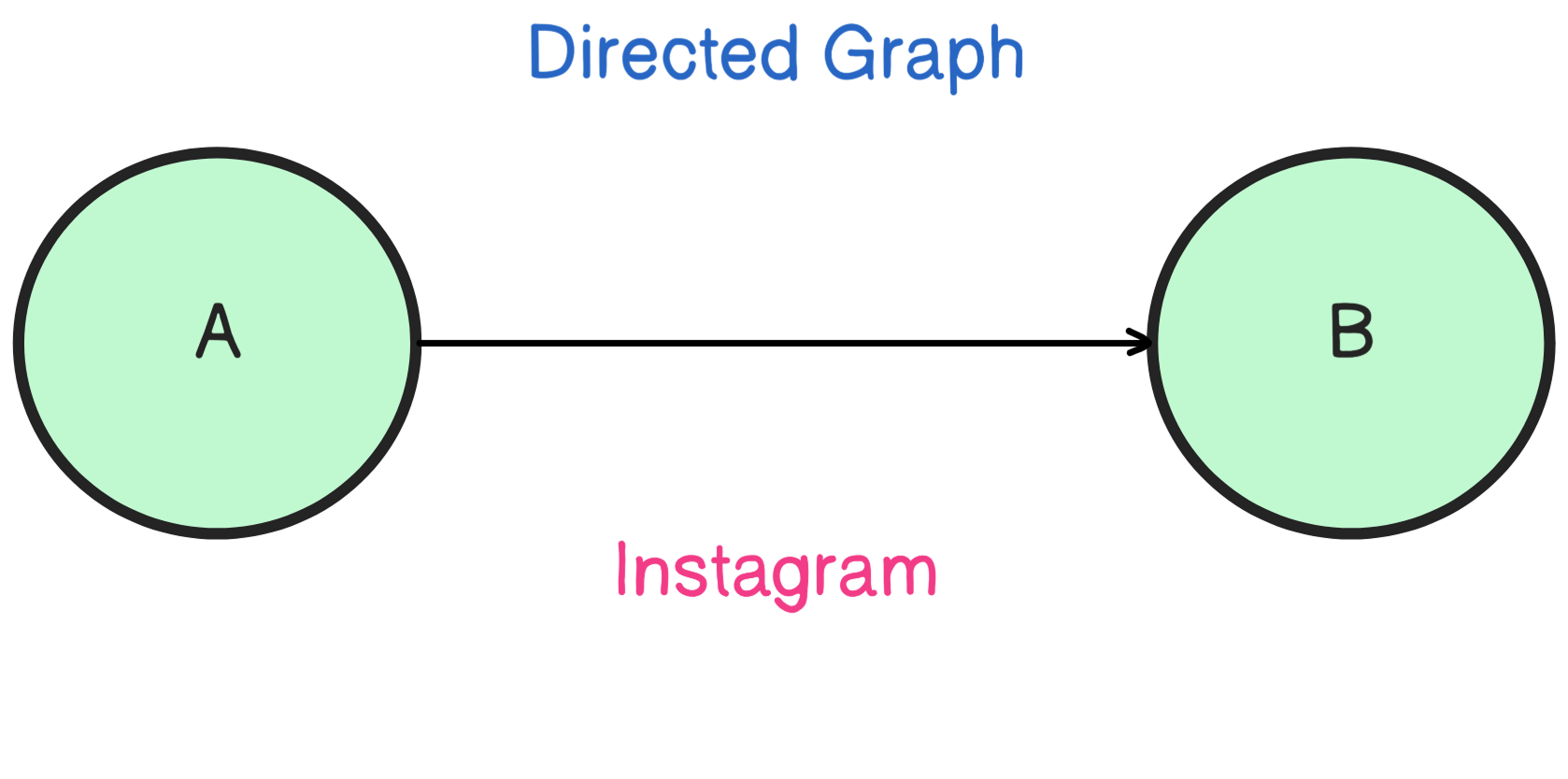
Think of something like Instagram: every user is a node, and every time you follow a user, you create a new edge connecting two nodes together.

This is known as a directed graph because the relationship flows one way—the follower follows the followed, and not vice‑versa.

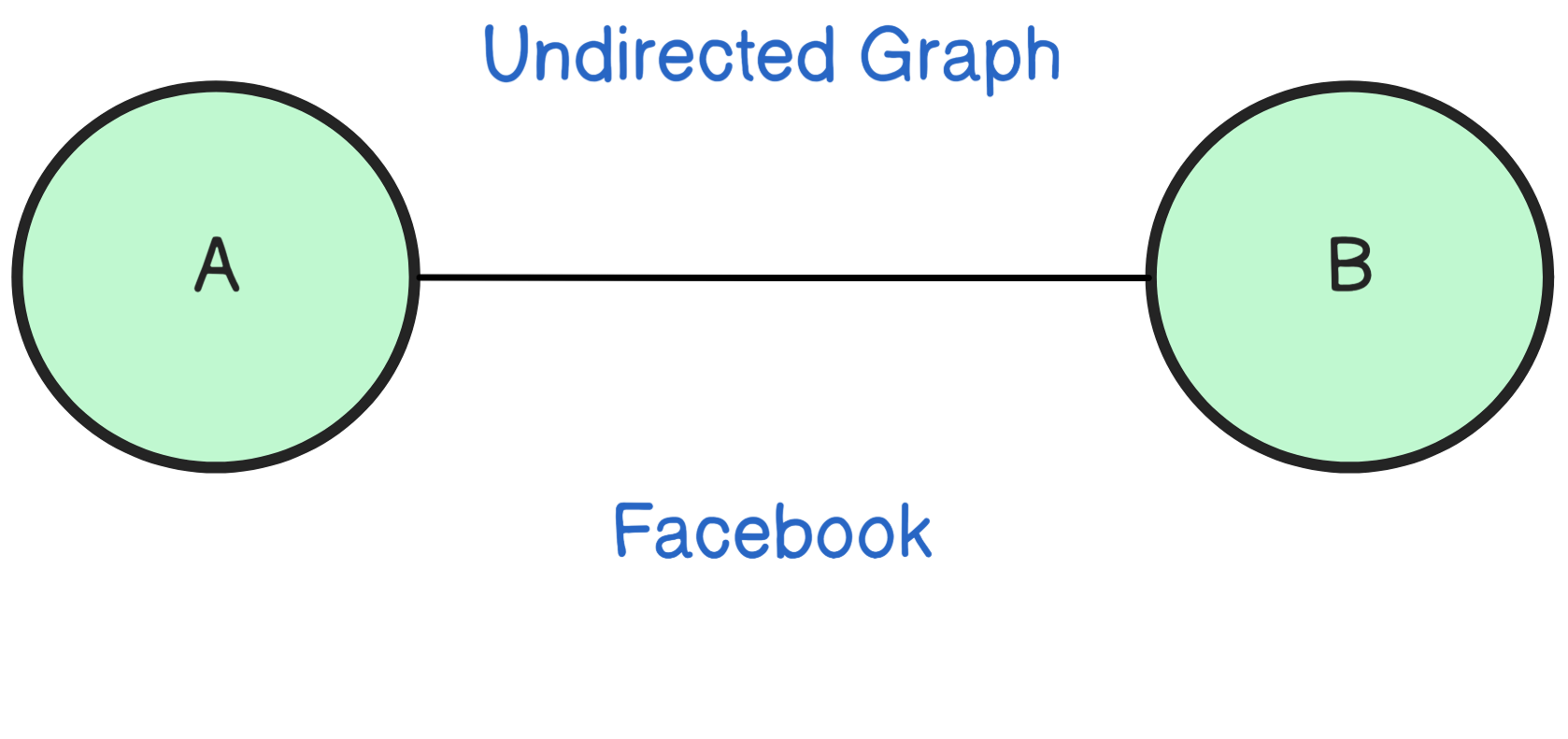
Now consider Facebook: your edges in the graph are friendships, and this relationship goes both ways, which is known as an undirected graph.

Graphs can also be weighted, which means the edge has some additional data about the relationship, like the distance between two airports.

A node might also point to itself, like an airplane that takes off and comes back to land at the same airport—this is known as a cycle.

When a directed graph has no cycles—that is, you can’t start at one node and eventually loop back—it’s called a Directed Acyclic Graph (DAG). DAGs are perfect for modeling hierarchical structures, where each link has a clear one‑way flow (for example, parent → child in a family tree).

One way to represent a graph in memory is with an adjacency matrix (a 2D array). You create one row and one column per node; if there’s an edge from node i to node j, you place a 1 at cell (i, j), otherwise a 0. This makes lookups for a specific edge extremely fast, but costs O(n²) space and even O(n²) time to insert a new node.

Example: Imagine three people: Alice (A), Bob (B), and Carol (C).

• Alice follows Bob

• Bob follows Carol

• Carol doesn’t follow anyone

The adjacency matrix would look like this:

    A B C

A [ 0 1 0 ]

B [ 0 0 1 ]

C [ 0 0 0 ]

Here, A→B and B→C, but no connection from C to anyone.

An alternative approach is an adjacency list: in this representation, we start with a collection of nodes, then each node has its array of its neighbours. This makes it faster to iterate over a node's edges and is more efficient with memory, especially when you have many nodes and few edges.

Example:

• Alice: follows Bob

• Bob: follows Carol

• Carol: follows no one

This is like:

• A → B

• B → C

• C → —

This format is much more space-efficient when most people follow only a few others. It's like everyone keeps a short list of their connections instead of filling out a big full table.

Applying Graph Concepts to a Family Tree

Let us now consider a DAG and apply it to something like family relationships:
Imagine a family tree—parents pointing to children.

• Parent → Child

• Grandparent → Parent

No loops are possible because a child can't point back to an ancestor. This makes DAGs ideal for modeling things like family trees, where a person can have one or more children, but no backward links to parents or ancestors.

Let's work with a concrete example. Imagine you have a scattered list of family members:

Continue Reading: Link