BFS and DFS of Graph traversal

BFS

Given a connected undirected graph containing V vertices, represented by a 2-d adjacency list adj[][], where each adj[i] represents the list of vertices connected to vertex i. Perform a Breadth First Search (BFS) traversal starting from vertex 0, visiting vertices from left to right according to the given adjacency list, and return a list containing the BFS traversal of the graph.

Note: Do traverse in the same order as they are in the given adjacency list. (Geeks)

Examples:

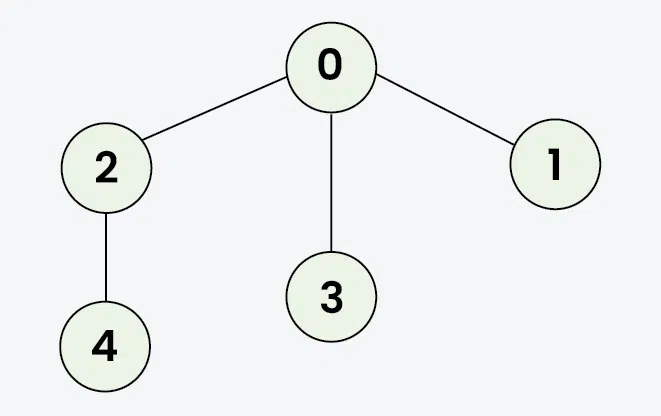
Input: adj[][] = [[2, 3, 1], [0], [0, 4], [0], [2]]

Output: [0, 2, 3, 1, 4]
Explanation: Starting from 0, the BFS traversal will follow these steps: 
Visit 0 → Output: 0 
Visit 2 (first neighbor of 0) → Output: 0, 2 
Visit 3 (next neighbor of 0) → Output: 0, 2, 3 
Visit 1 (next neighbor of 0) → Output: 0, 2, 3, 
Visit 4 (neighbor of 2) → Final Output: 0, 2, 3, 1, 4

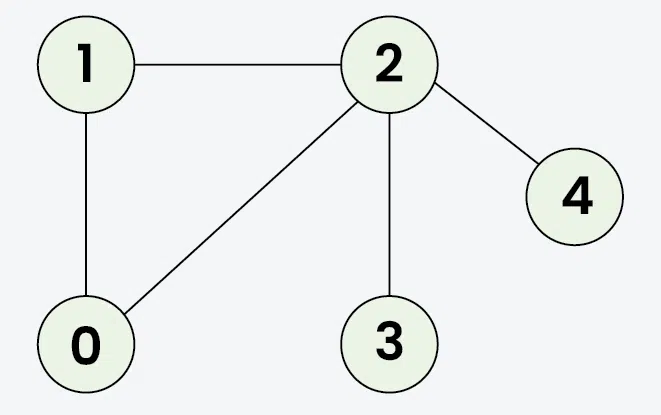
Input: adj[][] = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the BFS traversal proceeds as follows: 
Visit 0 → Output: 0 
Visit 1 (the first neighbor of 0) → Output: 0, 1 
Visit 2 (the next neighbor of 0) → Output: 0, 1, 2 
Visit 3 (the first neighbor of 2 that hasn't been visited yet) → Output: 0, 1, 2, 3 
Visit 4 (the next neighbor of 2) → Final Output: 0, 1, 2, 3, 4

Constraints: 1 ≤ V = adj.size() ≤ 10⁴
1 ≤ adj[i][j] ≤ 10⁴

BFS Algorithm

This is similar to a tree BFS traversal. In a tree, there are typically two nodes, left and right, but here there can be many. We store all the child nodes of a particular node in a queue, using a visited array to keep track. This helps avoid revisiting nodes that have already been connected back to a parent or have been visited before.

Time - O(n) + O(2xE)

Space - O(n)

class Solution {

    private void bfsTraversal(int vertex, ArrayList<ArrayList<Integer>> adj, 
                    int[] visited, ArrayList<Integer> ans){

        Queue<Integer> queue = new ArrayDeque<>();
        queue.add(vertex);
        visited[vertex] = 1;

        while(!queue.isEmpty()){
            int node = queue.poll();
            ans.add(node);
            for(int edgeVertex : adj.get(node)){
                if(visited[edgeVertex]!=1){
                    queue.add(edgeVertex);
                    visited[edgeVertex] = 1;
                }
            }
        }
    }

    public ArrayList<Integer> bfs(ArrayList<ArrayList<Integer>> adj) {

        ArrayList<Integer> ans = new ArrayList<>(); 
        int[] visited = new int[adj.size()];

        for(int vertex=0; vertex<adj.size(); vertex++){

            if(visited[vertex]!=1){
                bfsTraversal(vertex, adj, visited, ans);
            }
        }

        return ans;
    }
}

DFS

Given a connected undirected graph containing V vertices represented by a 2-d adjacency list adj[][], where each adj[i] represents the list of vertices connected to vertex i. Perform a Depth First Search (DFS) traversal starting from vertex 0, visiting vertices from left to right as per the given adjacency list, and return a list containing the DFS traversal of the graph. (Geeks)

Note: Do traverse in the same order as they are in the given adjacency list.

Examples:

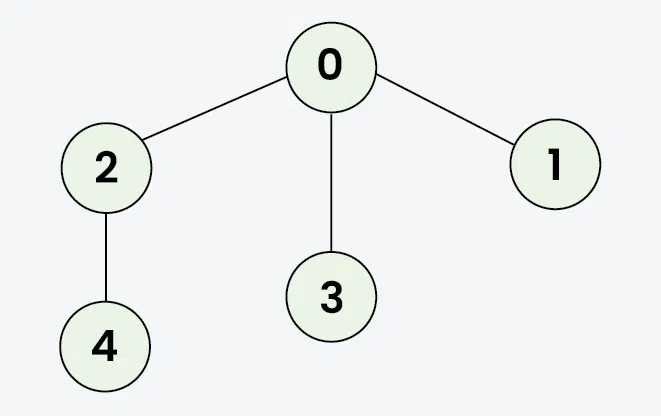
Input: adj[][] = [[2, 3, 1], [0], [0, 4], [0], [2]]

Output: [0, 2, 4, 3, 1]
Explanation: Starting from 0, the DFS traversal proceeds as follows:
Visit 0 → Output: 0 
Visit 2 (the first neighbor of 0) → Output: 0, 2 
Visit 4 (the first neighbor of 2) → Output: 0, 2, 4 
Backtrack to 2, then backtrack to 0, and visit 3 → Output: 0, 2, 4, 3 
Finally, backtrack to 0 and visit 1 → Final Output: 0, 2, 4, 3, 1

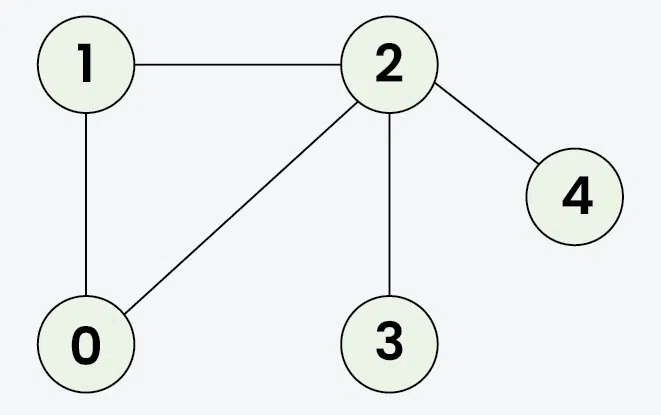
Input: adj[][] = [[1, 2], [0, 2], [0, 1, 3, 4], [2], [2]]

Output: [0, 1, 2, 3, 4]
Explanation: Starting from 0, the DFS traversal proceeds as follows: 
Visit 0 → Output: 0 
Visit 1 (the first neighbor of 0) → Output: 0, 1 
Visit 2 (the first neighbor of 1) → Output: 0, 1, 2 
Visit 3 (the first neighbor of 2) → Output: 0, 1, 2, 3 
Backtrack to 2 and visit 4 → Final Output: 0, 1, 2, 3, 4

Constraints:
1 ≤ V = adj.size() ≤ 10⁴
1 ≤ adj[i][j] ≤ 10⁴

DFS Algorithm

This is similar to a tree DFS traversal. In a tree, there are usually two nodes, left and right, but here there can be many. In tree DFS, we first fully explore the left side and then move to the right. Similarly, here we start with the first node in the adjacency list, fully explore its vertices, and then move to the next node in the list.

Time - O(n) + O(2xE)

Space - O(n) - Auxiliary space.

class Solution {

    private void dfsTraversal(int vertex, ArrayList<ArrayList<Integer>> adj, 
                int[] visited, ArrayList<Integer> ans){

        if(visited[vertex]==1) return;

        ans.add(vertex);
        visited[vertex]=1;

        for(int edgeVertex : adj.get(vertex)){
            dfsTraversal(edgeVertex, adj, visited, ans);
        }
    }

    public ArrayList<Integer> dfs(ArrayList<ArrayList<Integer>> adj) {
        ArrayList<Integer> ans = new ArrayList<>(); 
        int[] visited = new int[adj.size()];

        for(int vertex=0; vertex<adj.size(); vertex++){

            if(visited[vertex]!=1){
                dfsTraversal(vertex, adj, visited, ans);
            }
        }

        return ans;
    }
}