🧠 A Comprehensive Guide to Mastering Backtracking for Coding Interviews
 AlgoAvengers 🚀
AlgoAvengers 🚀
🚀 Welcome to another #TutorialTuesday with AlgoAvengers!
At AlgoAvengers, our #TutorialTuesday series is all about breaking down tough concepts into easily digestible tutorials. This time, we're going all-in on Backtracking, one of the most versatile techniques for solving complex algorithmic problems.
Backtracking is essential for solving problems involving combinations, permutations, constraint satisfaction, and exhaustive search. In this blog, you'll learn:
What backtracking is and how it works
A visual and intuitive understanding
A universal C++ template
Step-by-step explanation of real coding problems
Optimization techniques
Debugging tips and interview insights
Let’s dive right in!
🤖 What is Backtracking?
Backtracking is a problem-solving algorithm that builds up a solution incrementally and abandons a path as soon as it determines the path is invalid (i.e., doesn't satisfy constraints).
Think of it as a smart form of brute-force search that uses pruning to eliminate invalid or unnecessary paths early.
🛍️ Real-Life Analogy: Solving a Maze
Imagine you're trying to solve a maze:
You start walking down one path.
If you hit a dead end, you don't start from the beginning; you backtrack to the last decision point.
Then, you try a different path.
This is essentially what backtracking does: it tries all possible options in a recursive way but backtracks when it hits a constraint or invalid condition.
🔍 Why is it Useful?
Backtracking is widely used in problems like:
N-Queens
Sudoku Solver
Subset Generation
Permutations and Combinations
Word Search / Puzzle Solvers
It can solve problems that may have exponential complexity in a reasonable time thanks to pruning.
🌀 Backtracking vs. Plain Recursion
| Feature | Plain Recursion | Backtracking |
| Purpose | Explore all paths | Explore valid paths only |
| Efficiency | Inefficient | Prunes invalid paths early |
| Logic | No constraints | Includes constraints/pruning |
| Application | Basic problems | Complex constraint problems |
Key Difference: Backtracking adds an intelligent decision-making step (pruning) to plain recursion, helping avoid invalid states early.
🛠️ How Does Backtracking Work?
The backtracking approach uses the following steps:
Recursive Exploration: Explore from a starting point.
Decision Making: Choose an option from available ones.
Pruning: Check if the choice is valid.
Recurse: If valid, go deeper.
Backtrack: If invalid or done, undo the move.
Output Solution: If a full valid solution is found.
🌳 Visualizing a Decision Tree
Think of backtracking problems as a decision tree:
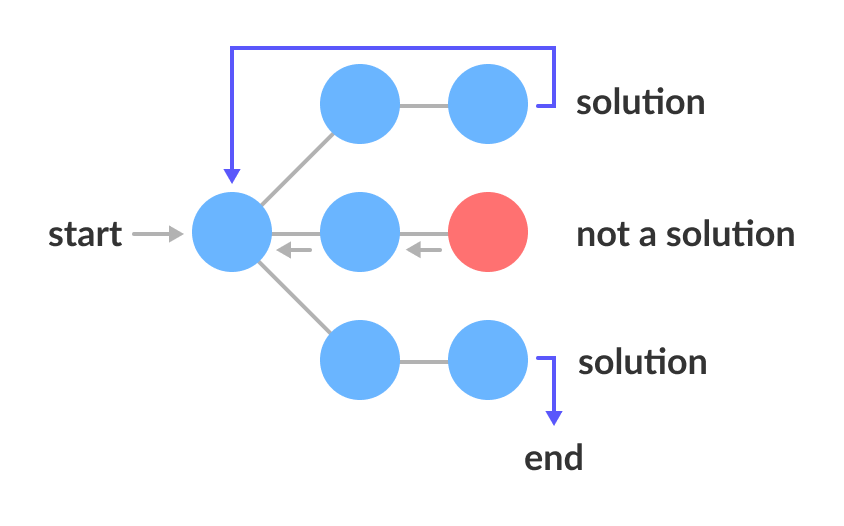
At each node, we try a choice. If valid, we go deeper; if invalid, we backtrack.
📈 Universal C++ Template
Here is a reusable structure you can adapt for any backtracking problem:
void solve(StateType &state, vector<StateType> &solutions) {
if (isBaseCase(state)) {
solutions.push_back(state);
return;
}
for (auto &choice : allPossibleChoices(state)) {
if (isValid(choice, state)) {
makeMove(state, choice);
solve(state, solutions);
undoMove(state, choice); // backtrack
}
}
}
🔎 Explanation
isBaseCase(state): The stopping condition (e.g., all queens placed).isValid(...): Checks if the move/choice obeys the problem constraints.makeMove/undoMove: Responsible for adding/removing the effect of a choice (i.e., backtrack).
We'll refer back to this template while explaining the problems below.
📌 Common Backtracking Problems with Explanation
1. Generating All Subsets (Power Set)
The goal here is to find every possible subset of a given set of numbers. For example, if the input is [1, 2, 3], the subsets are [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3].
The key idea is that for each element in the input array, you have two choices: either include it in your current subset or don't. Backtracking lets you explore both of these paths.
void helper(vector<int>& nums, int index, vector<int>& path, vector<vector<int>>& res) {
// 💡 Base Case:
// This is the point where we've considered every element up to the end of the array.
// The 'path' vector now represents a complete subset, so we add it to our results.
res.push_back(path);
// 🔄 Recursive Exploration with Choices:
// The for-loop is where we make our choices.
// We iterate from the current 'index' to the end of the array.
for (int i = index; i < nums.size(); i++) {
// ➡️ Make a move:
// We decide to include the current number `nums[i]` in our path.
path.push_back(nums[i]);
// 🧠 Recurse:
// Now, we recursively call the helper function to explore subsets that
// include `nums[i]`. We pass `i + 1` to ensure we don't consider
// the same element again in the same path, and to move on to the next element.
helper(nums, i + 1, path, res);
// ⏪ Backtrack (Undo the move):
// After the recursive call returns, it means we have explored all
// possible subsets that contain `nums[i]`. To explore other possibilities
// (those that *don't* contain `nums[i]`), we must undo our last move.
// This is the "backtracking" step where we remove the element we just added.
path.pop_back();
}
}
Template Mapping:
isBaseCase(state): In this specific problem, we add the currentpathto the solution at the beginning of each recursive call. The loop's conditioni < nums.size()acts as the termination for exploring new choices.makeMove(state, choice):path.push_back(nums[i]);undoMove(state, choice):path.pop_back();
2. Permutations of a List
The goal is to find every possible arrangement (permutation) of the elements in a list. For [1, 2, 3], the permutations are [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], and [3, 2, 1].
The core logic is to fix one element at a time and then recursively find all permutations of the remaining elements.
void permuteHelper(vector<int>& nums, int index, vector<vector<int>>& res) {
// 💡 Base Case:
// When the `index` reaches the size of the array, it means we have
// successfully filled every position. The 'nums' array now holds a complete
// permutation, so we add a copy of it to our results.
if (index == nums.size()) {
res.push_back(nums);
return;
}
// 🔄 Recursive Exploration with Choices:
// The for-loop iterates through the remaining elements to choose which one
// to place at the current `index`.
for (int i = index; i < nums.size(); i++) {
// ➡️ Make a move:
// We swap the element at the current `index` with the element at `i`.
// This effectively "chooses" `nums[i]` to be at this position.
swap(nums[index], nums[i]);
// 🧠 Recurse:
// We make a recursive call for the next position (`index + 1`).
// The rest of the array will now be permuted.
permuteHelper(nums, index + 1, res);
// ⏪ Backtrack (Undo the move):
// We swap the elements back to their original positions. This is crucial
// because it resets the array to the state it was in before the last
// choice, allowing us to explore other options for the current `index`.
swap(nums[index], nums[i]);
}
}
Template Mapping:
isBaseCase(state):index == nums.size()makeMove(state, choice):swap(nums[index], nums[i]);undoMove(state, choice):swap(nums[index], nums[i]);(Swapping twice returns the array to its original state).
3. N-Queens Problem
The goal is to place N queens on an N x N chessboard so that no two queens can attack each other (i.e., no two queens share the same row, column, or diagonal).
The backtracking approach places one queen per row. For each row, it tries to place a queen in every column. If a position is safe, it places the queen and moves to the next row. If no safe column is found in the current row, it backtracks to the previous row and tries a different column.
// 🔍 isValid: Check if placing a queen at `(row, col)` is safe.
// This function checks the current column and both diagonals to see if
// another queen is already present.
bool isSafe(vector<string>& board, int row, int col) {
// Check column
for (int i = 0; i < row; i++) {
if (board[i][col] == 'Q') return false;
}
// Check top-left diagonal
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q') return false;
}
// Check top-right diagonal
for (int i = row - 1, j = col + 1; i >= 0 && j < board.size(); i--, j++) {
if (board[i][j] == 'Q') return false;
}
return true;
}
void solveNQueens(vector<string>& board, int row, vector<vector<string>>& solutions) {
// 💡 Base Case:
// If we have successfully placed a queen in every row (`row == board.size()`),
// it means we've found a valid solution.
if (row == board.size()) {
solutions.push_back(board);
return;
}
// 🔄 Recursive Exploration with Choices:
// For the current row, we iterate through every possible column.
for (int col = 0; col < board.size(); col++) {
// 🛡️ Pruning (isValid check):
// Before making a move, we check if placing a queen here is safe.
// This is the core of backtracking—we prune invalid paths early.
if (isSafe(board, row, col)) {
// ➡️ Make a move:
// If the position is safe, place a queen ('Q').
board[row][col] = 'Q';
// 🧠 Recurse:
// Move to the next row to place the next queen.
solveNQueens(board, row + 1, solutions);
// ⏪ Backtrack (Undo the move):
// After the recursive call returns (either a solution was found or
// a dead end was reached), we reset the current cell to be empty ('.').
// This is essential to explore other column choices for the current row.
board[row][col] = '.';
}
}
}
Template Mapping:
isBaseCase(state):row == board.size()isValid(choice, state):isSafe(board, row, col)makeMove(state, choice):board[row][col] = 'Q';undoMove(state, choice):board[row][col] = '.';
4. Subset Generation (Using Include/Exclude)
This is an alternative way to solve the subset problem, showcasing a different style of backtracking where the choices are made in the recursive calls themselves, rather than in a loop.
void findSubsets(vector<int>& nums, int index, vector<int>& current, vector<vector<int>>& result) {
// 💡 Base Case:
// When we've considered every element in the array, the `current` vector
// represents a valid subset, which we add to our results.
if (index == nums.size()) {
result.push_back(current);
return;
}
// ➡️ Choice 1: Include the current element.
// Make a move: Add the element at `index` to our current subset.
current.push_back(nums[index]);
// Recurse: Explore paths that include this element by moving to the next index.
findSubsets(nums, index + 1, current, result);
// Backtrack: Remove the element to reset the state for the next choice.
current.pop_back();
// ➡️ Choice 2: Exclude the current element.
// Recurse: We simply call the function for the next index, but without
// adding `nums[index]` to the `current` path.
findSubsets(nums, index + 1, current, result);
}
Template Mapping:
isBaseCase(state):index == nums.size()makeMove(state, choice):current.push_back(nums[index]);undoMove(state, choice):current.pop_back();
5. Sudoku Solver
The objective is to fill a 9x9 Sudoku grid with digits 1-9 such that each number appears only once in each row, column, and 3x3 subgrid.
This is a classic backtracking problem. The algorithm finds the first empty cell, tries to place a number from 1 to 9 in it. If a number is valid according to Sudoku rules, it places it and moves on to the next empty cell. If it gets stuck, it backtracks and tries a different number.
// 🔍 isValid: Checks if placing a number is valid according to Sudoku rules.
bool isValid(vector<vector<int>>& board, int row, int col, int num) {
// Check row and column
for (int i = 0; i < 9; i++) {
if (board[row][i] == num || board[i][col] == num) return false;
}
// Check 3x3 subgrid
int startRow = 3 * (row / 3), startCol = 3 * (col / 3);
for (int r = startRow; r < startRow + 3; r++) {
for (int c = startCol; c < startCol + 3; c++) {
if (board[r][c] == num) return false;
}
}
return true;
}
bool solveSudoku(vector<vector<int>>& board) {
// 🔄 Recursive Exploration with Choices:
// We iterate through the entire board to find the first empty cell.
for (int row = 0; row < 9; row++) {
for (int col = 0; col < 9; col++) {
// If we find an empty cell (value 0)
if (board[row][col] == 0) {
// Try numbers 1-9 as choices
for (int num = 1; num <= 9; num++) {
// 🛡️ Pruning (isValid check)
if (isValid(board, row, col, num)) {
// ➡️ Make a move
board[row][col] = num;
// 🧠 Recurse: Move to the next empty cell.
// If this path leads to a solution, we return true.
if (solveSudoku(board)) return true;
// ⏪ Backtrack (Undo the move)
// If the recursive call returns false, it means this
// choice didn't lead to a solution. We reset the cell
// and try the next number in the loop.
board[row][col] = 0;
}
}
// If we've tried all numbers 1-9 and none worked,
// it means the previous choice was wrong. Backtrack!
return false;
}
}
}
// 💡 Base Case:
// If the loops complete without finding any empty cells, it means the board
// is fully solved and valid. We return true to signal success.
return true;
}
Template Mapping:
isBaseCase(state): When the loops finish without finding an empty cell.isValid(choice, state):isValid(board, row, col, num)makeMove(state, choice):board[row][col] = num;undoMove(state, choice):board[row][col] = 0;
6. Grid Paths (Right or Down)
The problem is to find all possible paths from the top-left corner (0, 0) to the bottom-right corner (m-1, n-1) of a grid, moving only right ('R') or down ('D').
This is a great example of a simple backtracking problem where the choices are fixed and simple.
void findPaths(int r, int c, int m, int n, string path, vector<string>& allPaths) {
// 💡 Base Case:
// We've reached the destination. The `path` string holds a complete path.
if (r == m - 1 && c == n - 1) {
allPaths.push_back(path);
return;
}
// 🔄 Recursive Exploration with Choices:
// Choice 1: Move Down
// 🛡️ Pruning: Check if we can move down (i.e., we are not at the last row).
if (r < m - 1) {
// 🧠 Recurse: Make a recursive call for the next cell `(r + 1, c)`
// and append 'D' to the current `path`.
findPaths(r + 1, c, m, n, path + "D", allPaths);
}
// Choice 2: Move Right
// 🛡️ Pruning: Check if we can move right (i.e., we are not at the last column).
if (c < n - 1) {
// 🧠 Recurse: Make a recursive call for the next cell `(r, c + 1)`
// and append 'R' to the current `path`.
findPaths(r, c + 1, m, n, path + "R", allPaths);
}
// ❗ Note on Backtracking:
// In this specific problem, we don't need an explicit `undoMove` step.
// The `path` string is passed by value (`path + "D"` creates a new string),
// so it doesn't modify the state of the caller's `path` variable.
// This effectively handles the backtracking by discarding the extended path
// once the function call returns.
}
Template Mapping:
isBaseCase(state):r == m - 1 && c == n - 1isValid(choice, state):r < m - 1andc < n - 1makeMove(state, choice):path + "D"orpath + "R". The new string is created implicitly.undoMove(state, choice): Thepathstring is not modified in-place, so backtracking is handled automatically when the function returns.
⚖️ Optimization Techniques
Pruning: Avoid invalid states early.
Heuristics: Try promising options first (e.g., fill most constrained cell).
Memoization: Save results of subproblems (backtracking + DP).
Bitmasking: For space-efficient representation of state.
🔧 Debugging Tips
Use dry runs with small inputs.
Print recursion call stack.
Understand base vs. backtrack condition.
Visualize the decision tree.
Comment and isolate sections to test independently.
🧳 Conclusion
Backtracking is a powerful recursive approach that gives you the flexibility to explore all possibilities while also optimizing the search with pruning. It’s essential for coding interviews and understanding combinatorial problem solving.
Start simple, master the universal template, and then build confidence with practice!
💬 Connect With Us!
🐦 Telegram: https://t.me/Free_Courses_N_Internships
💼 LinkedIn: AlgoAvengers
Thanks for reading 📖
Subscribe to my newsletter
Read articles from AlgoAvengers 🚀 directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

AlgoAvengers 🚀
AlgoAvengers 🚀
AlgoAvengers is a dev-first platform delivering curated tech news, career tips, and job updates — daily. We post theme-based blogs 7 days a week, covering: 💡 Dev concepts 🧠 Career & motivation 🔧 Tools & resources 📰 Weekly tech news (#FinalCommit) Join 8k+ developers growing with clarity, not chaos. 🚀