CS50 AI with Python – Lecture 0: Search – Problem Set 0: Tic-tac-toe
 Shichun Min
Shichun Min
Preface
Successfully completed Degrees, which really boosted my confidence. Riding the momentum, I'm moving on to the second assignment: Tic-Tac-Toe.
Introduction
Tic-tac-toe, also known as noughts and crosses, is a simple two-player game. Despite its simplicity, it serves as a perfect example to demonstrate adversarial search algorithms.
In CS50’s Introduction to Artificial Intelligence with Python, this project is the first hands-on exercise after learning about search algorithms. The goal is to build an unbeatable AI opponent using the Minimax algorithm.
Requirements Analysis
Implement an AI player for Tic-Tac-Toe in Python with the following requirements:
Represent the game state using
X,O, andEMPTY.Players take turns making moves.
The AI player must use the Minimax algorithm to ensure it always chooses the optimal move.
The game should handle end-of-game conditions, including wins and draws.
In theory, you should never beat the AI; if it wins, check your algorithm.
The Pygame framework for the game is already provided— so I only need to implement the game logic.
Problem Abstraction
This is a classic adversarial search problem, which can be modeled as follows:
State: Tic-Tac-Toe is a 3×3 board where each cell is X, O, or EMPTY. It can be easily represented using a 2D list. Look like this:
# Board as a 3x3 list board = [ ["X", "O", "EMPTY"], ["EMPTY", "X","EMPTY"], ["EMPTY", "EMPTY", "O"] ]Action: A player's move can be abstracted as modifying the board—changing one EMPTY cell in the 2D list to X or O.
State Transition: A new board state is generated based on the current player's chosen move.
Goal: Determine the next board state according to the current player's move.
Utility:
X wins,return +1
O wins,return-1
Draw,return 0
Core Algorithm Design
The Minimax algorithm is an adversarial search method that models winning conditions as scores: one player aims for -1, while the other aims for +1. Future moves are guided by these scores: the Min player tries to achieve the lowest score, and the Max player tries to achieve the highest score.
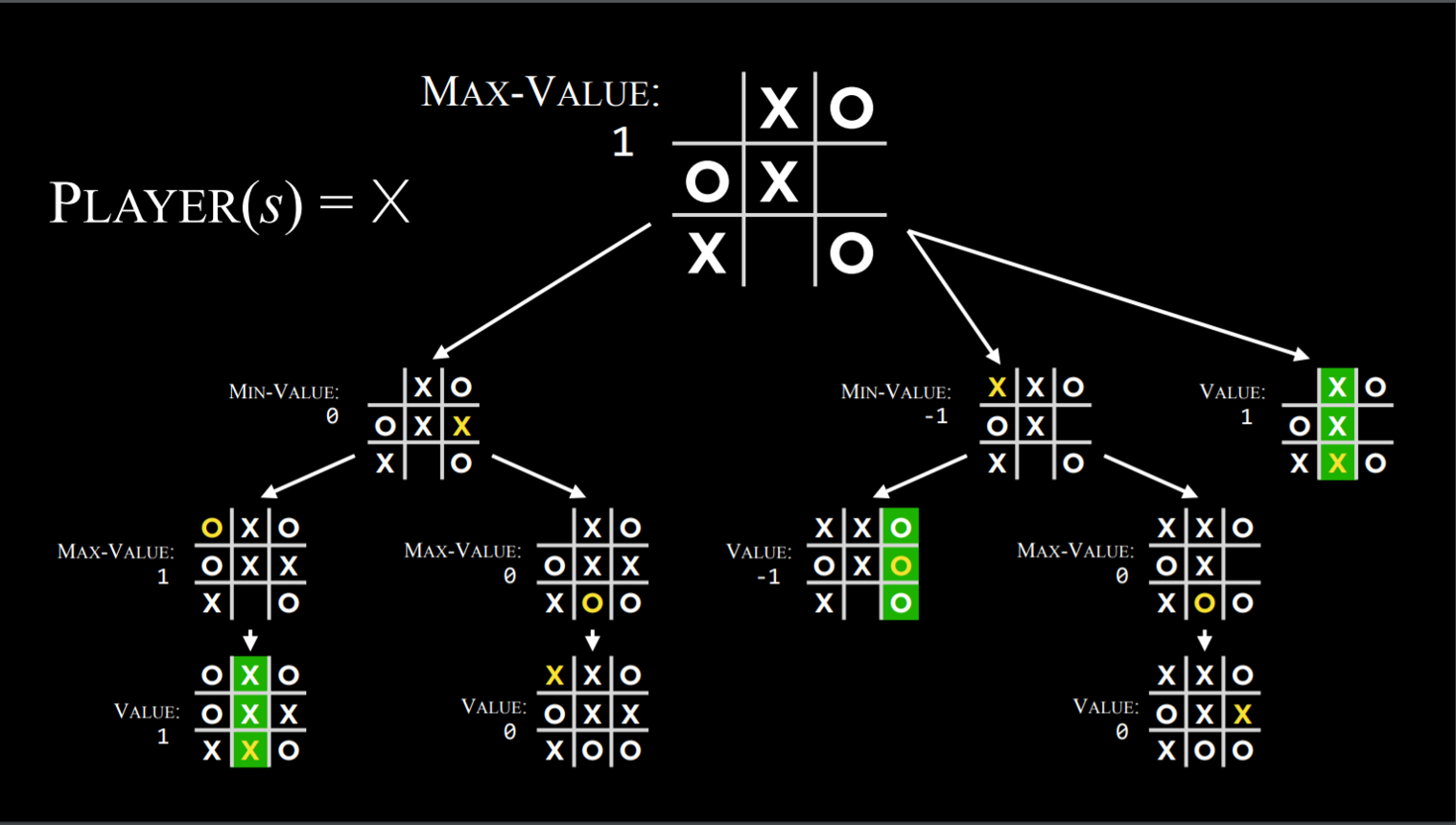
Basic Idea of Minimax
Termination Conditions:
- If the current board state is terminal (win, loss, or draw), return the utility value immediately.
Max player(X)’s turn:
Iterate through all possible moves.
Recursively call Minimax for each move.
Select the move with the highest returned value.
Min player(O)’s trun:
Iterate through all possible moves.
Recursively call Minimax for each move.
Select the move with the lowest returned value.
Code implementation
tictactoe.py
"""
Tic Tac Toe Player
"""
import math
import copy
X = "X"
O = "O"
EMPTY = None
def initial_state():
"""
Returns starting state of the board.
"""
return [[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY],
[EMPTY, EMPTY, EMPTY]]
def player(board):
"""
Returns player who has the next turn on a board.
"""
num_x = 0
num_o = 0
for row in board:
for element in row:
if element == X:
num_x += 1
elif element == O:
num_o += 1
# X always play first, so if X is more than O, then O's turn
return O if num_x > num_o else X
def actions(board):
"""
Returns set of all possible actions (i, j) available on the board.
"""
possible_actions = set()
for i in range(len(board)):
for j in range(len(board[i])):
if board[i][j] == EMPTY:
possible_actions.add((i, j))
return possible_actions
def result(board, action):
"""
Returns the board that results from making move (i, j) on the board.
"""
# check if action is valid
if len(action) != 2:
raise ValueError("Invalid action length")
i, j = action
if not (0 <= i < len(board) and 0 <= j < len(board[i])):
raise ValueError("Action out of range")
if board[i][j] != EMPTY:
raise ValueError("Cell is not empty")
new_board = copy.deepcopy(board)
new_board[i][j] = player(board)
return new_board
def winner(board):
"""
Returns the winner of the game, if there is one.
"""
# check rows
for row in board:
if row[0] == row[1] == row[2] != EMPTY:
return row[0]
#check columns
for col in range(3):
if board[0][col] == board[1][col] == board[2][col] != EMPTY:
return board[0][col]
# check two diagonals
if board[0][0] == board[1][1] == board[2][2] != EMPTY:
return board[0][0]
if board[0][2] == board[1][1] == board[2][0] != EMPTY:
return board[0][2]
# No winner
return None
def terminal(board):
"""
Returns True if game is over, False otherwise.
"""
# Winner exist, game over
if winner(board) is not None:
return True
# No empty cells, game over
elif all(cell != EMPTY for row in board for cell in row):
return True
else:
return False
def utility(board):
"""
Returns 1 if X has won the game, -1 if O has won, 0 otherwise.
"""
w = winner(board)
if w == X:
return 1
elif w == O:
return -1
else:
return 0
def minimax(board):
"""
Returns the optimal action for the current player on the board.
"""
# Game is over, no more actions
if terminal(board):
return None
current_player = player(board)
best_action = None
# Max player, try to get the highest score
if current_player == X:
best_score = -math.inf
for action in actions(board):
# O player will take action, and he/she will minimize score
score = min_value(result(board, action))
if score > best_score:
best_score = score
best_action = action
# Min player, try to get the lowest score
else:
best_score = math.inf
for action in actions(board):
# X player will take action, and he/she will maximize score
score = max_value(result(board, action))
if score < best_score:
best_score = score
best_action = action
return best_action
def max_value(board):
"""
return max value of new board result if you take the action,
Min player need to get the max value, because Min player know
than Max player will give him/her the max value
"""
if terminal(board):
return utility(board)
best_score = -math.inf
for action in actions(board):
# For each action that min player will take,
# he/she will choose the minimal score
score = min_value(result(board, action))
# All those values min player give me, I will pick up
# a maximal one
best_score = max(best_score, score)
return best_score
def min_value(board):
"""
return min value of new board result if you take the action,
Max player need to get the min value, because Max player know
than Min player will give him/her the min value
"""
if terminal(board):
return utility(board)
best_score = math.inf
for action in actions(board):
# For each action that max player will take,
# he/she will choose the maximal score
score = max_value(result(board, action))
# All those values max player give me, I will pick up
# a minimal one
best_score = min(best_score, score)
return best_score
Implementation Outcome
The AI never loses
It prioritizes moves that lead to a win (+1 score).
If no winning move is available, it blocks the opponent’s winning move, resulting in a draw (0 score).
Afterthoughts
The biggest challenge in the Tic-Tac-Toe project was the recursive implementation. The Minimax algorithm needs to consider all possible moves at each step, assuming the opponent will also make the optimal move. Each level of recursion switches between the Max player and the Min player, accurately checks for terminal states, and backtracks the board state.
Although the state space is small and recursion is feasible, this exercise gave me an intuitive understanding of the core ideas of adversarial search, allowed me to appreciate the elegance of handling multi-level decision-making, and laid the foundation for optimizing algorithms in more complex games. Through this project, I truly experienced the power of AI in strategic decision-making.
Tic-Tac-Toe only has 9 cells, so there are at most 9! possible board states. Using Minimax is feasible here.
However, for games with many more possible states, like chess, it’s impossible to explore all possibilities because the number of states can reach around 10²⁹⁰⁰⁰.
In such cases, optimization techniques like Alpha-Beta pruning are necessary to greatly improve search efficiency.
This assignment is just an introductory exercise in adversarial search, but it lays the theoretical foundation for more complex adversarial search algorithms.
By watching the course videos, summarizing the lecture notes, and carefully completing the assignments, I gained a solid understanding of the core ideas behind search algorithms and took my first step into the world of AI algorithms.
Moving forward, I’m starting Lecture 1.
Subscribe to my newsletter
Read articles from Shichun Min directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
