Undirected Graph Cycle (DFS | BFS)

Problem

Given an undirected graph with V vertices and E edges, represented as a 2D vector edges[][], where each entry edges[i] = [u, v] denotes an edge between vertices u and v, determine whether the graph contains a cycle or not. The graph can have multiple component. (geeks link)

Examples:

Input: V = 4, E = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 3]]
Output: true
Explanation:

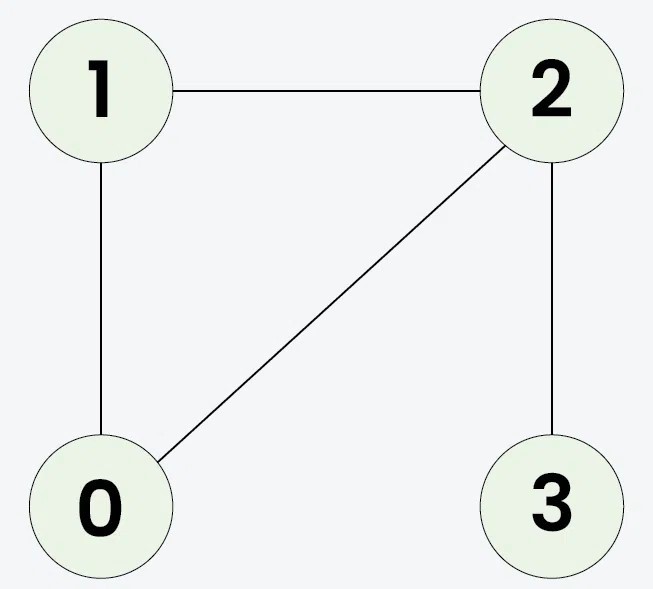
1 -> 2 -> 0 -> 1 is a cycle.

Input: V = 4, E = 3, edges[][] = [[0, 1], [1, 2], [2, 3]]
Output: false
Explanation:

No cycle in the graph.

Constraints: 1 ≤ V ≤ 10⁵
1 ≤ E = edges.size() ≤ 10⁵

Solution

Idea: It's simple. We use the traversal technique BFS/DFS. If we find that a node is already visited, then there is a cycle. Otherwise, there isn't. Note that we exclude checking the parent node because, in an undirected graph, we can also go back along the same edge.

BFS

class Solution {

    public boolean isCycle(int V, int[][] edges) {
        List<List<Integer>> adjList = createAdjList(V, edges);
        int[] visited = new int[V];

        for(int vertex=0; vertex<V; vertex++){

            if(visited[vertex]==0 && bfs(vertex, adjList, visited)){
                return true;
            }
        }
        return false;
    }

    public boolean bfs(int i, List<List<Integer>> adjList, int[] visited){

        Queue<Pair<Integer, Integer>> queue = new ArrayDeque<>();
        queue.add(new Pair<>(i, -1));

        while(!queue.isEmpty()){
            Pair<Integer, Integer> pair = queue.poll();
            int node = pair.vertex;
            int parentNode = pair.parentVertex;
            visited[node] = 1;

            for(int edgeVertex : adjList.get(node)){
                if(edgeVertex == parentNode){
                    continue;
                }

                if(visited[edgeVertex]==0){
                    queue.add(new Pair<>(edgeVertex, node));
                    visited[edgeVertex] = 1;
                }
                else{
                    return true;
                }
            }
        }
        return false;
    }


    private List<List<Integer>> createAdjList(int V, int[][] edges){
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i=0; i<V; i++){
            adjList.add(new ArrayList<>());
        }

        for(int[] edge : edges){
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        return adjList;
    }

    class Pair <A, B>{
        A vertex;
        B parentVertex;

        Pair(A vertex, B parentVertex){
            this.vertex = vertex;
            this.parentVertex = parentVertex;
        }

        @Override
        public String toString() {
            return "Pair{" +
                   "vertex=" + vertex +
                   ", parentVertex=" + parentVertex +
                   '}';
        }
    }
}

DFS

class Solution {
    public boolean isCycle(int V, int[][] edges) {
        List<List<Integer>> adjList = createAdjList(V, edges);
        int[] visited = new int[V];

        for(int vertex=0; vertex<V; vertex++){

            if(visited[vertex]==0 && dfs(vertex, -1, adjList, visited)){
                return true;
            }
        }
        return false;
    }

    public static boolean dfs(int i, int parentVertex, List<List<Integer>> adjList, int[] visited){

        if(visited[i]==1){
            return true;
        }

        visited[i]=1;

        for(int adjVertex : adjList.get(i)){
            if(adjVertex != parentVertex && dfs(adjVertex, i, adjList, visited)){
                return true;
            }
        }
        return false;
    }

    private static List<List<Integer>> createAdjList(int V, int[][] edges){
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i=0; i<V; i++){
            adjList.add(new ArrayList<>());
        }

        for(int[] edge : edges){
            adjList.get(edge[0]).add(edge[1]);
            adjList.get(edge[1]).add(edge[0]);
        }

        return adjList;
    }

}