Directed Graph Cycle (DFS | BFS)

Problem

Given a Directed Graph with V vertices (Numbered from 0 to V-1) and E edges, check whether it contains any cycle or not.
The graph is represented as a 2D vector edges[][], where each entry edges[i] = [u, v] denotes an edge from verticex u to v. (geeks)

Examples:

Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3]]

Output: true
Explanation: The diagram clearly shows a cycle 0 → 2 → 0

Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 3]

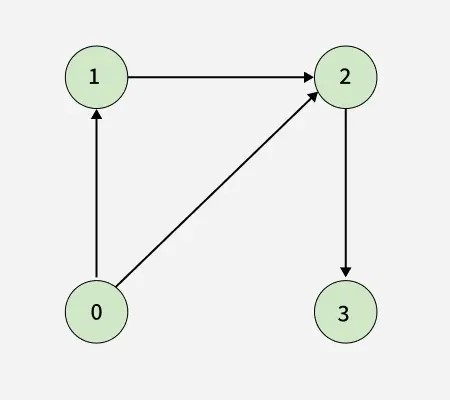
Output: false
Explanation: no cycle in the graph

Constraints:
1 ≤ V, E ≤ 10⁵
u ≠ v

Solution

DFS

Idea: We use the DFS algorithm with an additional path visited array. The reason is that if we rely only on the visited array, we might reach a particular node through another path that is not a cycle in a directed graph, but in an undirected graph, it is definitely a cycle.

Time - O(V+E)

Space - O(2V)

class Solution {
    public boolean isCyclic(int V, int[][] edges) {
        List<List<Integer>> adjList = createAdjList(V, edges);
        int[] visited = new int[V];
        int[] pathVisited = new int[V];

        for(int i=0; i<V; i++){

            if(dfs(i, visited, pathVisited, adjList)){
                return true;
            }
        }
        return false;
    }

    private boolean dfs(int i, int[] visited, int[] pathVisited, List<List<Integer>> adjList){

        if(visited[i]==1) {
            if(pathVisited[i] == 1) return true;
            return false;
        }

        visited[i] = 1;
        pathVisited[i] = 1;
        for(int edgeVertex : adjList.get(i)){

            if(dfs(edgeVertex, visited, pathVisited, adjList)){
                return true;
            }
        }

        pathVisited[i] = 0;
        return false;
    }

    private List<List<Integer>> createAdjList(int V, int[][] edges){
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i=0; i<V; i++){
            adjList.add(new ArrayList<>());
        }

        for(int[] edge : edges){
            adjList.get(edge[0]).add(edge[1]);
        }

        return adjList;
    }

}

BFS (kahn’s Algorithm Application)

We use Kahn’s Algorithm. If the order we find is not the same as the total number of vertices, we say there is a cycle in the graph.

Time - O(V+E)

Space - O(V)

class Solution {
    public boolean isCyclic(int V, int[][] edges) {
        List<List<Integer>> adjList = createAdjList(V, edges);
        int[] indegrees = createIndegrees(V, edges);
        Queue<Integer> queue = createQueue(indegrees);

        List<Integer> order = new ArrayList<>();
        while(!queue.isEmpty()){
            int vertex = queue.poll();
            order.add(vertex);

            for(int adjVertex : adjList.get(vertex)){
                indegrees[adjVertex]-=1;
                if(indegrees[adjVertex]==0){
                    queue.add(adjVertex);
                }
            }
        }

        return order.size()!=V;
    }

    private static Queue<Integer> createQueue(int[] indegrees){
        Queue<Integer> queue = new ArrayDeque<>();
        for(int vertex=0; vertex<indegrees.length; vertex++){
            if(indegrees[vertex]==0){
                queue.add(vertex);
            }
        }
        return queue;
    }

    private static int[] createIndegrees(int V, int[][] edges) {
        int[] indegrees = new int[V];
        for(int[] edge : edges){
            indegrees[edge[1]]+=1;
        }
        return indegrees;
    }

    private static List<List<Integer>> createAdjList(int V, int[][] edges){
        List<List<Integer>> adjList = new ArrayList<>();
        for(int i=0; i<V; i++){
            adjList.add(new ArrayList<>());
        }

        for(int[] edge : edges){
            adjList.get(edge[0]).add(edge[1]);
        }

        return adjList;
    }

}