Binary Search Trees: Implementation and Practical Applications

Binary search trees (BSTs) are a fundamental data structure commonly used in computer science, offering several advantages over traditional and linked lists. Unlike linear structures, BSTs provide logarithmic time complexity for critical operations, making them highly efficient for searching, insertion, and deletion operations. BSTs are also used to implement other data structures, such as heaps and priority queues.

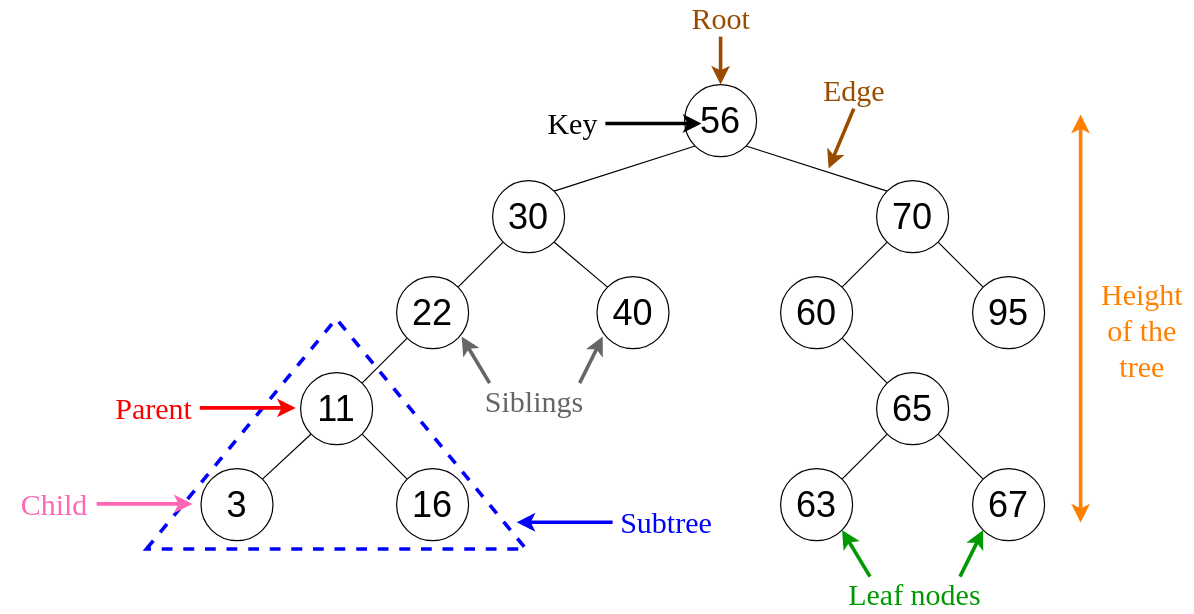
Advantages of Binary Search Trees Over Lists and Linked Lists:

1. Efficient Search Operations: In a binary search tree, each node has two children - a left child with a smaller value and a right child with a larger value. This hierarchical structure allows efficient searching by eliminating half of the remaining nodes at each step. In contrast, linear structures like lists require sequential searches, resulting in linear time complexity. Time Complexity: O(log n) for BSTs vs. O(n) for lists.

   

2. Ordered Data Storage: Binary search trees inherently maintain order, with elements stored in a way that allows quick retrieval in a sorted sequence. This ordering property simplifies tasks such as finding the minimum or maximum element, locating the successor or predecessor of a given element, and performing range queries. Time Complexity: O(log n) for tasks like finding min/max or predecessor/successor.

3. 

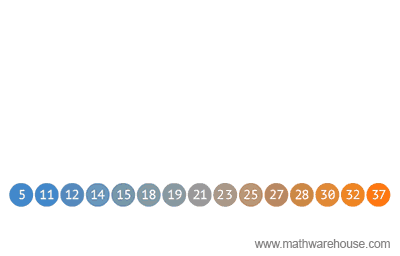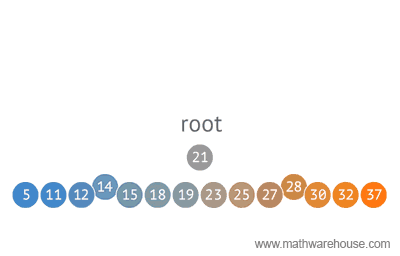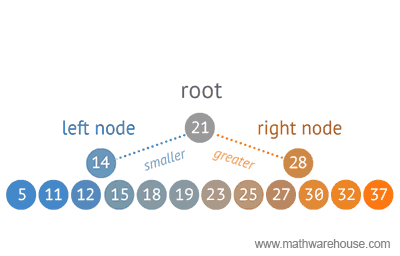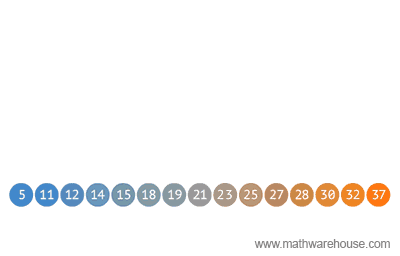
   Dynamic Size Adjustments: Unlike arrays, binary search trees can dynamically adjust their size without requiring memory reallocation. This flexibility is particularly advantageous when dealing with datasets that grow or shrink over time, as the structure efficiently adapts to changes. Time Complexity: Still O(log n) for insertion and deletion.

Despite their advantages, BSTs also have some disadvantages. For some applications, BSTs are less efficient than other data structures, such as hash tables. For example, BSTs are less efficient than hash tables for storing key-value pairs.

Examples of efficiency gains in using binary search trees:

1. Dictionary implementation: Binary search trees are commonly used in dictionary and associative array implementations. The ordered nature of BSTs facilitates quick searches, making them ideal for situations where quick access to key-value pairs is critical.

2. Database Indexing: In database systems, binary search trees are used for indexing, improving the speed of search queries. This is especially advantageous in large databases where quickly retrieving records based on specific criteria is critical.

3. Symbol table in compilers: Compilers use symbol tables to store and manage variable names and their corresponding attributes.

The following algorithm can be used to build a binary search tree:

1. Create an empty tree.

2. Insert the first element into the tree.

3. To insert an element into the BST, compare it to the root node's value:

   If the element is equal to the value of the root node, then the element is already in the tree, and you do nothing. If the element is less than the value of the root node, insert the element into the left subtree of the root node. If the element is greater than the value of the root node, insert the element into the right subtree of the root node.

To use a binary search tree, you can use the following methods:

• Insert(item): Insert an item into the tree.

• Search (item): Finds an item in the tree and returns True if the item is found and False if not.

• Delete (item): Removes an element from the tree.

Let's build a code for building the binary tree:

class Node:
    def __init__(self, data):
        self.data=data
        self.left_node=None
        self.right_node=None

class BinarySearchTree:
    def __init__(self):
        #we can access the root node exclusively
        self.root =None
    def insert(self, data):
        if self.root is None:
            #binary search tree is empty
            self.root=Node(data)
            #now the binary search tree is not empty
        else:
            self.insert_node(data,self.root)
            #implement a function to insert data starting with the root
    def insert_node(self, data, node):
           #all the data that is smaller than the given node will be in the left subtree, and all the data that is bigger than the given node will be in the right subtree
        if data <node.data:
            if node.left_node:
                #if the left child exists, we keep going and try to find a valid location for the data 
                self.insert_node(data, node.left_node)
            else: 
                #if the left child does not exist we create it
                node.left_node = Node(data,node)
        #we have to go to the right subtree

By constructing and using binary search trees, developers can create powerful and structured data structures suitable for various applications, ultimately improving the performance of multiple algorithms and systems.