I first began to doubt the historical validity of Mecca when reading the works of Dan Gibson, an archaeologist who grew up in the Middle East. By the Jordanian Government's authority, he was tasked with researching and producing a historical report on the Nabateans, an ancient civilisation of Nomadic traders who had a large presence in the Middle East. They were known for their clever navigation skills which allowed them to bring goods from the Mediterranean, across the Arabian desert and the Gulf, to Asia. Dan Gibson spent 25 years visiting ancient sites, temples and landmarks known to be occupied by the Nabateans.

Nabateans and Bedouins

Ancient Arab navigators, also known as Bedouins, used the same methods as the Nabateans to navigate across the changing sand dunes. They adeptly used the North Star, or Polaris, to guide their travels across the vast and featureless sand dunes. They employed a simple, yet ingenious wooden device called a "kamal," which consisted of a rectangular piece of wood and a string with knots. By holding the kamal at arm's length and aligning it with the horizon and the North Star, they could determine their latitude based on the number of knots visible between the horizon and the star. This rudimentary tool helped them maintain a consistent direction during their night journeys. Additionally, the Bedouins recited poetry with a measured rhythm to track the distance they had walked. Each verse of the poem represented a specific distance, allowing them to estimate their travel over time. This combination of astronomical observation and poetic tradition enabled them to navigate effectively across the changing and shifting desert landscapes.

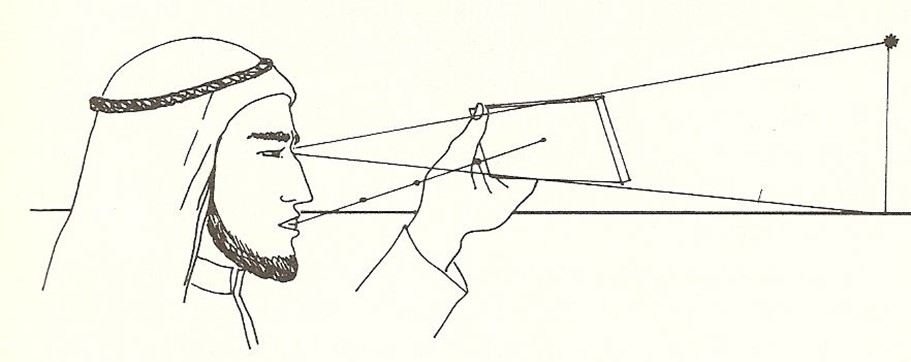
Combining these techniques, they could accurately locate towns, trade centres, water wells, and other landmarks. By knowing the latitudinal position of these critical locations, they could navigate the desert with remarkable precision, ensuring they reached vital points for rest, trade, and sustenance. This was also the method they used to accurately determine the direction of prayer.

Enter Dan Gibson: The 'Archaeologist's Archaeologist'

As a side project on his travels, he also examined, the architecture of ancient mosques. Gibson, using the ATLAS navigation satellites, built by the Japanese, pinpointed to the highest precision the location and bearing of each mosque. Gibson noted that the ancient mosques were not facing Mecca, but rather a different location. He arrived at a mosque, found the Qibla wall and the mirhrab, and pointed his navigation compass directly perpendicular to the wall.

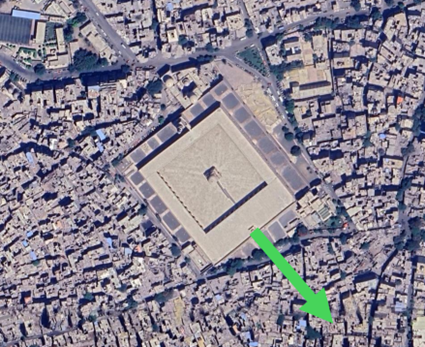
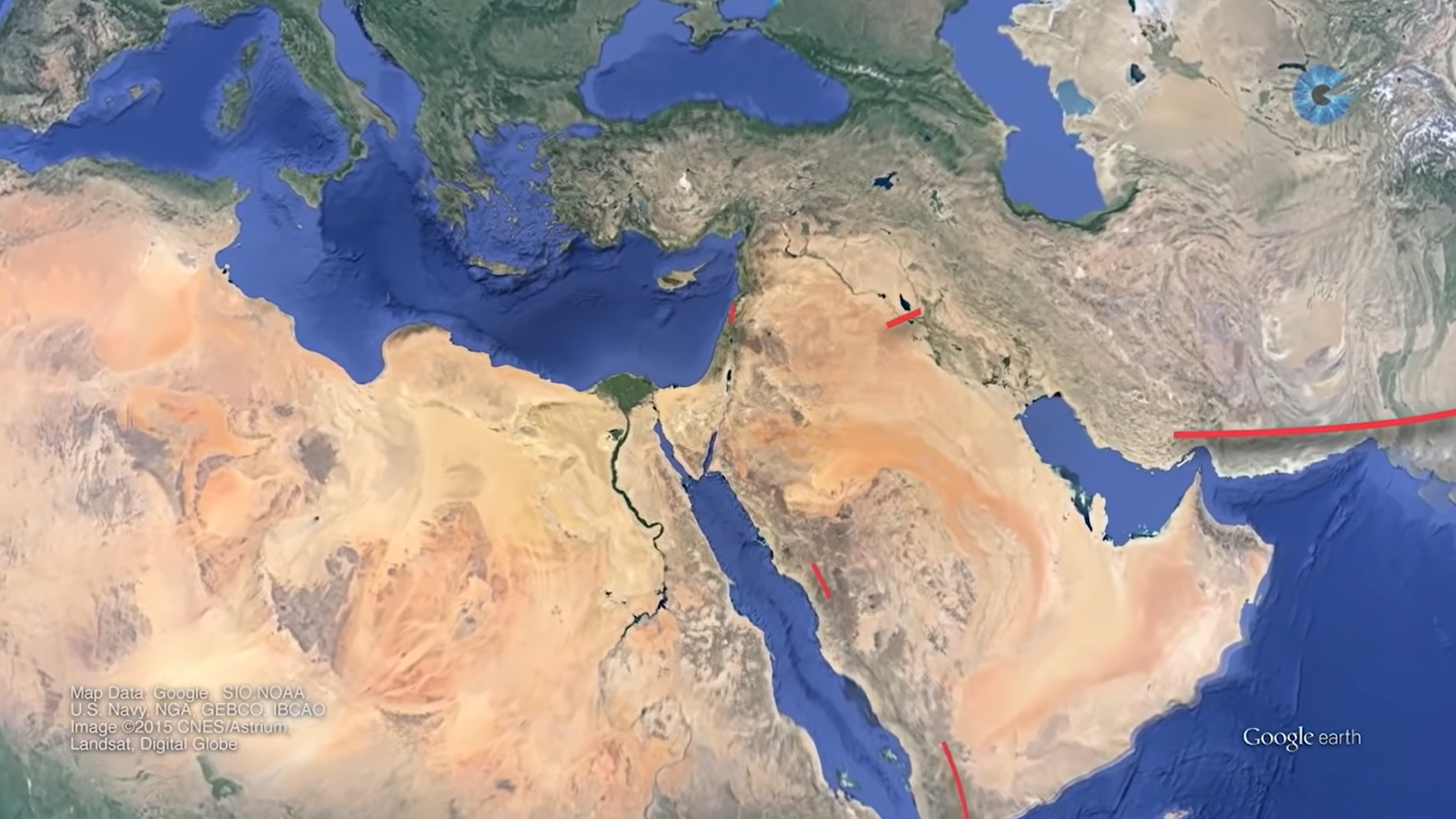
For example, the Ibn Tulun Mosque in Egypt, built in 876 AD, is oriented to 145.4°:

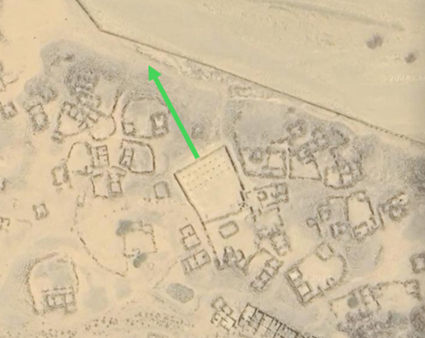
The Abu Dulaf Mosque in Iraq, built in 859 AD, is orientated to 191.57°.

The Asham Mosque, built in 9th century, in Saudi Arabia is orientated to 332.2°

Every mosque, according to the Islamic tradition, has foundations oriented towards the Masjid Al-Haram. Many Qiblas are very difficult to find today because many mosques have been destroyed and built again, and so the original floor plans have been lost. Nonetheless, we can use our archaeological and detective skills to understand where the original Qibla wall is. Typically, the qibla wall is the longest side of the mosque and features a small space for the imam to be situated, known as a ‘mihrab’, when leading the prayer.

Since Dan Gibson's remarkable publications, the historical validity of the Islamic faith has come into question. In fact, nowhere in the original Hadiths or the Quran mention the words "Mecca" in regards to the direction of prayer. The words "Masjid Al-Haram" is referred to as the direction of prayer, but the word "Mecca" is never mentioned. It is only merely used as an insertion [Mecca] by translators and scholars. Furthermore, while the Saudis undergo huge renovations to the Al-Haram: digging deep into the ground before laying huge foundations, they have not found any artefacts, structures or evidence of the Quraysh tribes, which are said to have lived in Mecca. Rather, the only structure they have found belongs to the Ottoman Empire, hundreds of years too late.

So this begs the question: where is the Masjid Al-Haram, if it is not Mecca?

Spherical Geometry and the Great Circle

In this analysis, we can make use of the directions of the qiblas of different mosques. By drawing a line from the mosques, we can determine the point of intersection which each of them are facing.

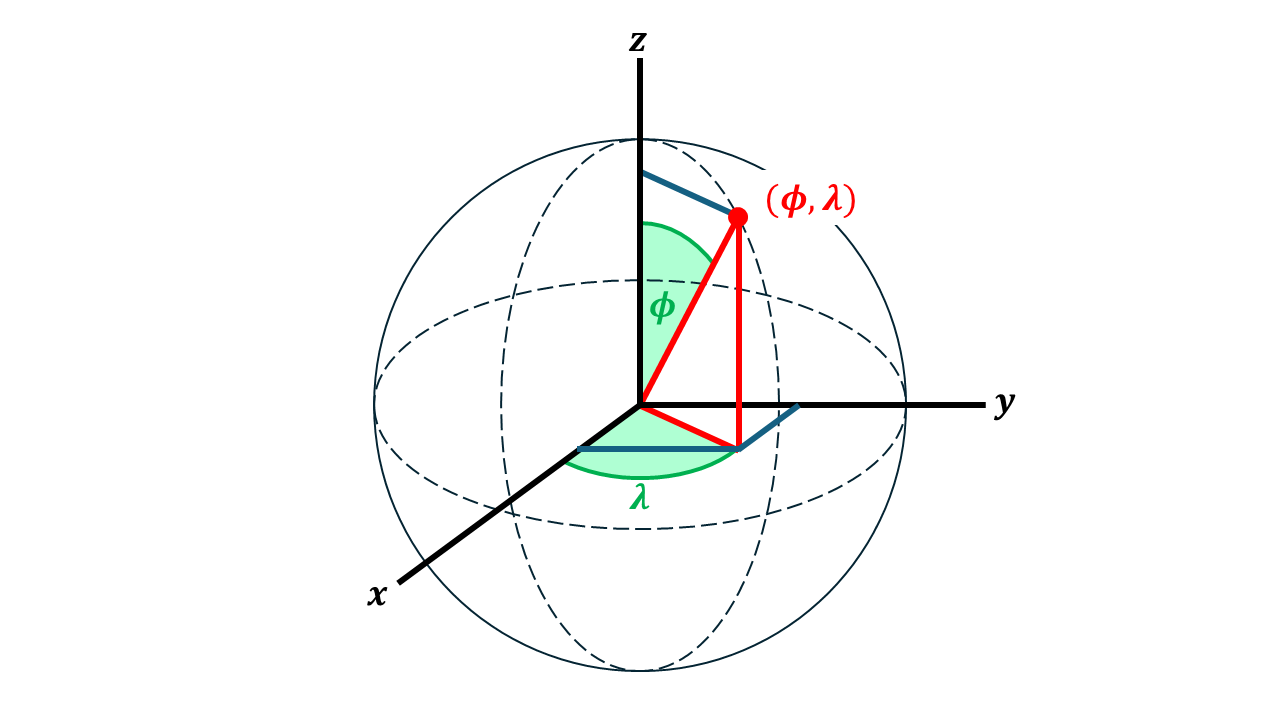
Just like Cartesian coordinates, whereby a position in space is specified by the (x, y, z) coordinates, you can also define a position in space using (r, θ, φ), where r is the distance from the origin, θ is the polar angle from the z-axis and φ is the azimuthal angle from the x-axis. On the Earth's surface, which is assumed to be a sphere of constant radius r, we use spherical coordinates in terms of the latitude (Φ) and longitude (λ).

We can transfer these coordinates into Cartesian coordinates for a unit sphere:

Similarly, we can define vectors on this sphere in Cartesian space at different longitude and latitude points. The North and East vectors may be defined as:

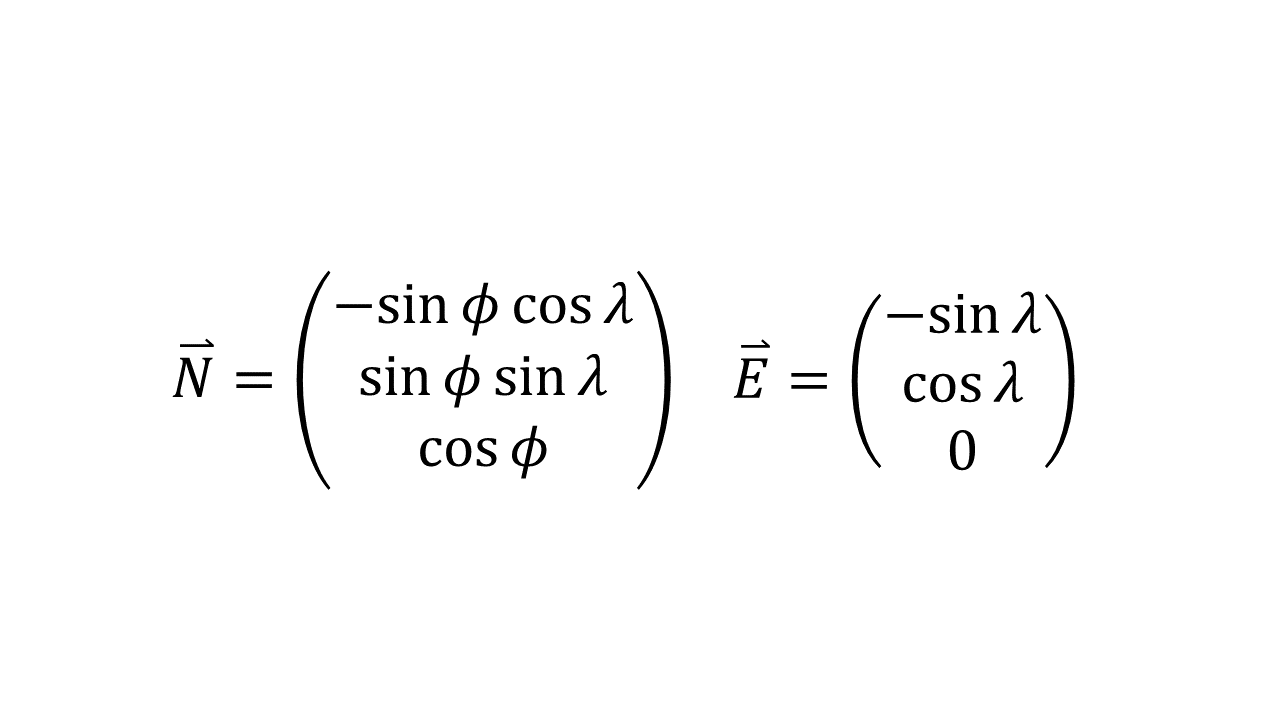
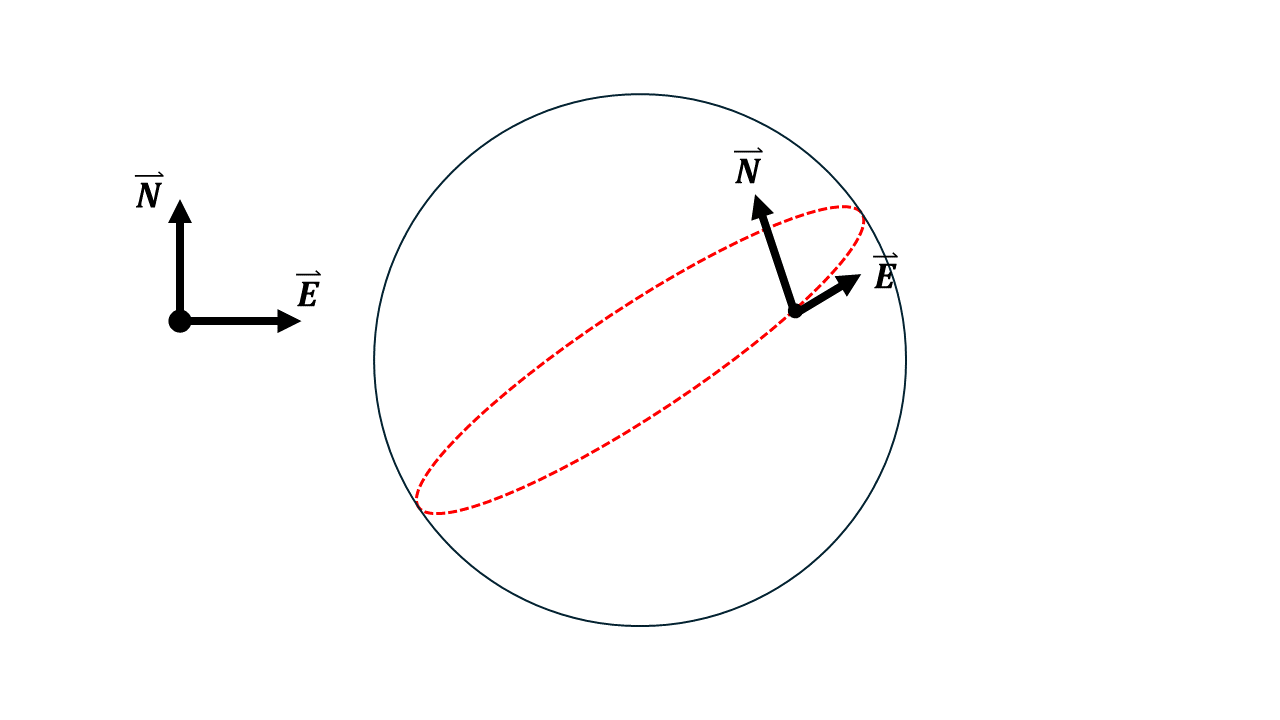
Given that we can define the North and East vectors, we can therefore resolve a vector which sums to the direction vector of where our mosque is facing, given any bearing from North, θ:

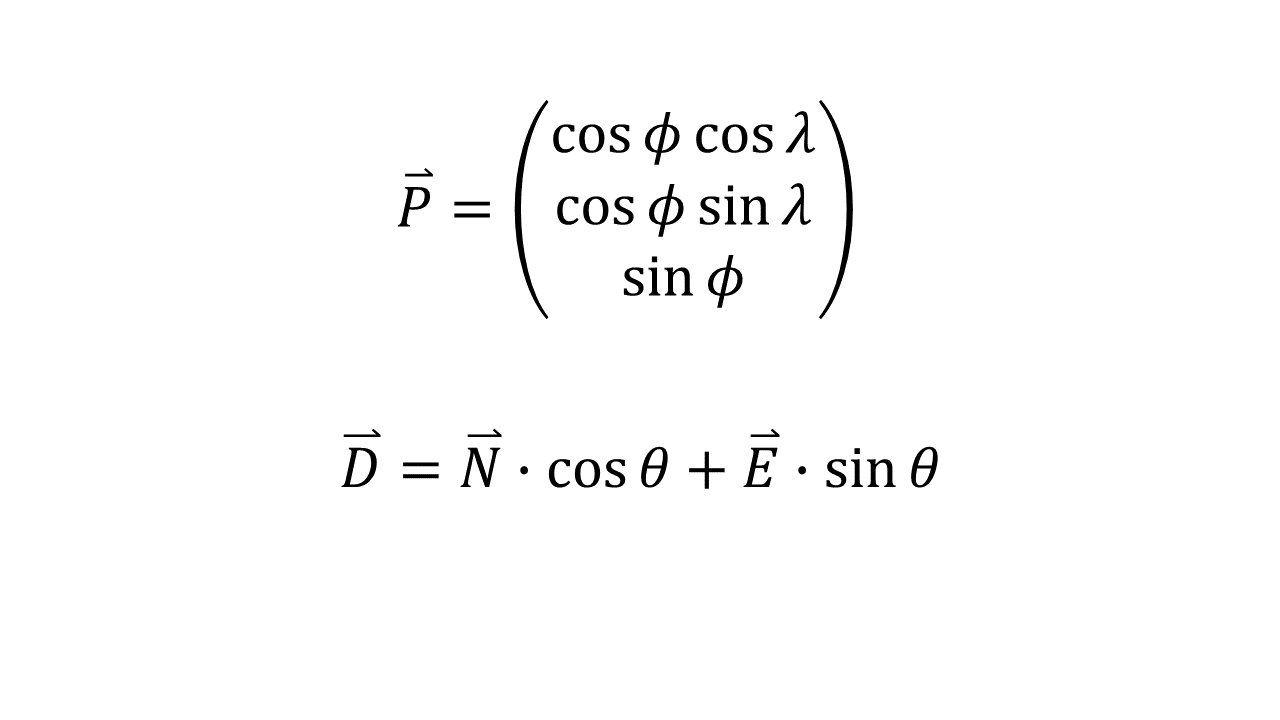
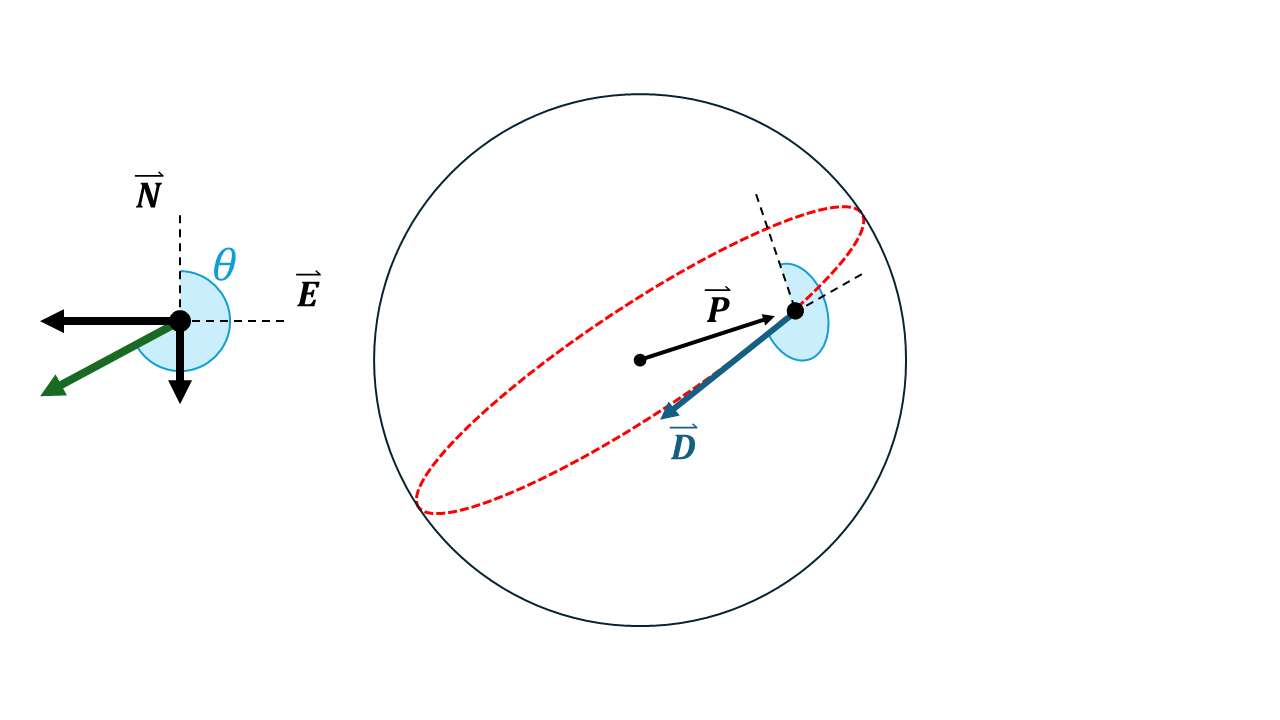
Given that both the position P can be a position vector P, coupled with a direction vector D, we can take the cross product of both of these vectors to find the perpendicular face vector F. The face vector F is perpendicular to the Great Circular which is drawn around the sphere from the position P in the direction D.
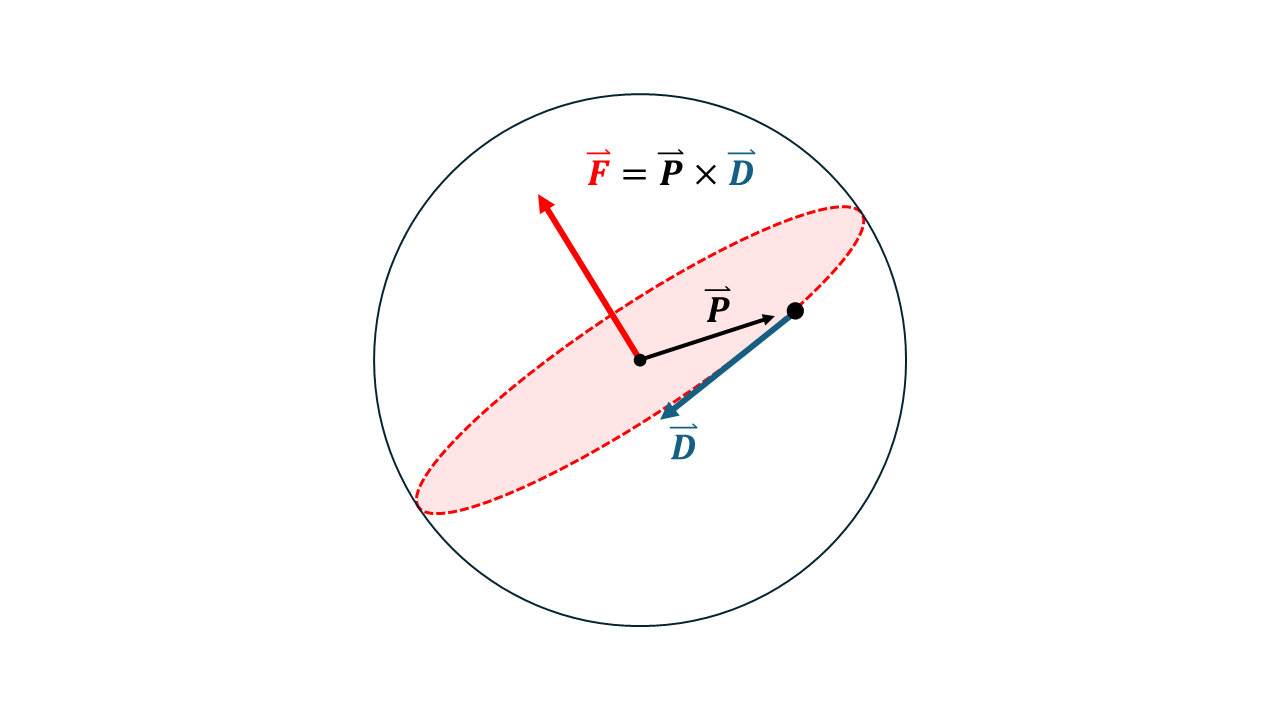
Furthermore, we can repeat steps 1-4 for another mosque with position (Φ,λ) and bearing from North, θ.

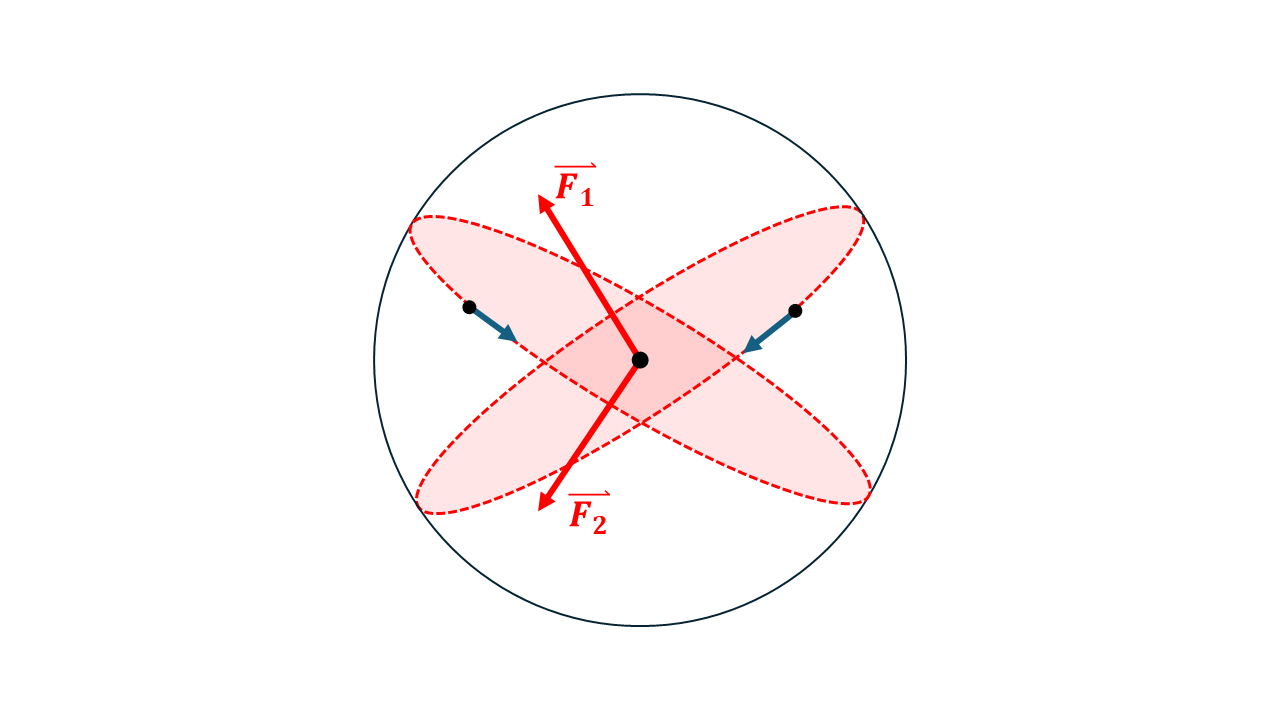
In order to find where these two circles intersect, we can find the cross product between the two face vectors, giving us a vector which lies perpendicular to the face vectors and along the line of intersection.

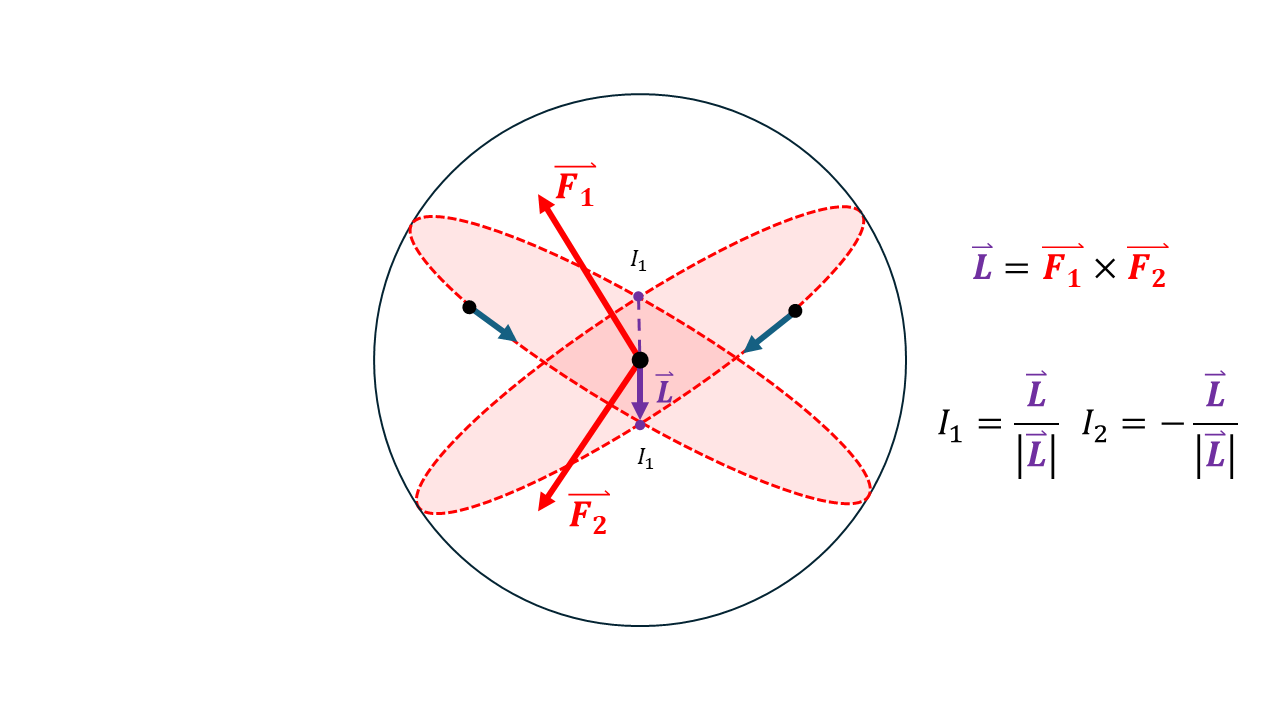
Since the lines intersect at two points, we will generate two solutions; and because we know that the Masjid Al-Haram does not lie at the opposite side of the globe in the Pacific Ocean, we can reject points which are out of bounds of where we are interested in.

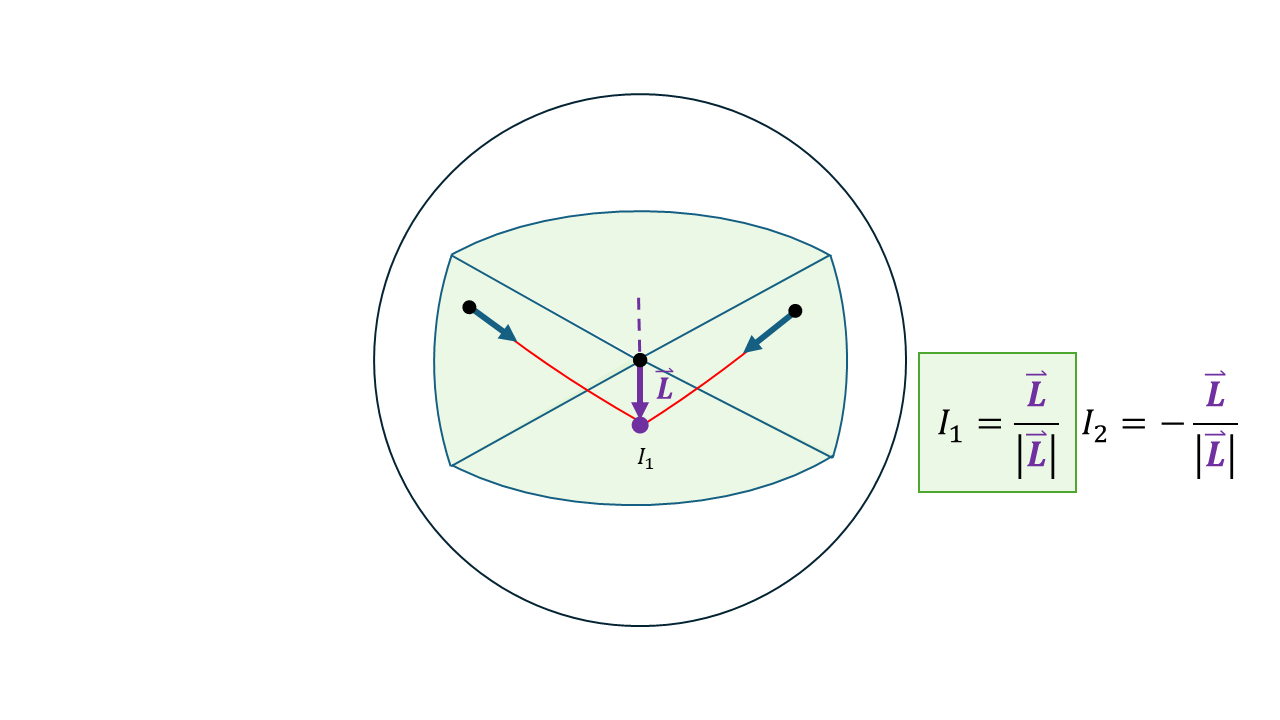
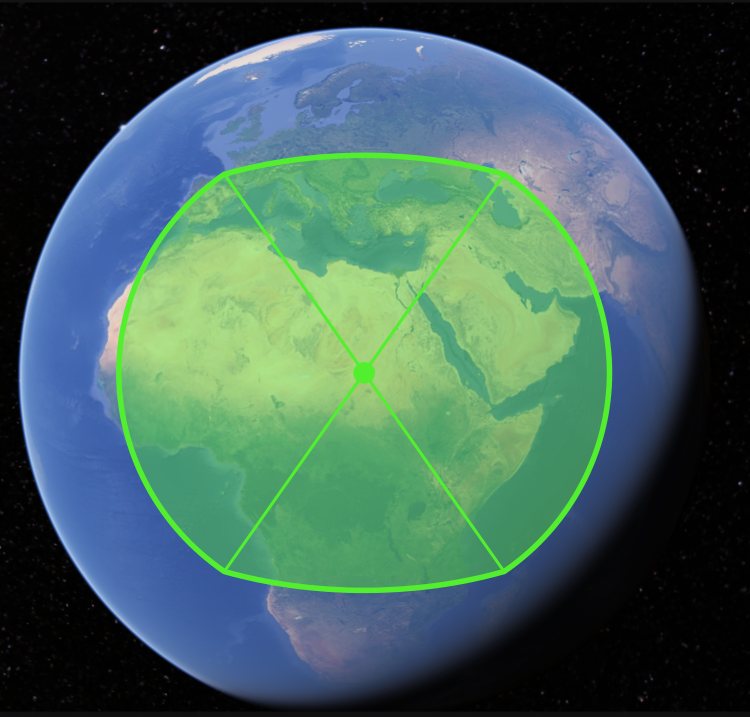
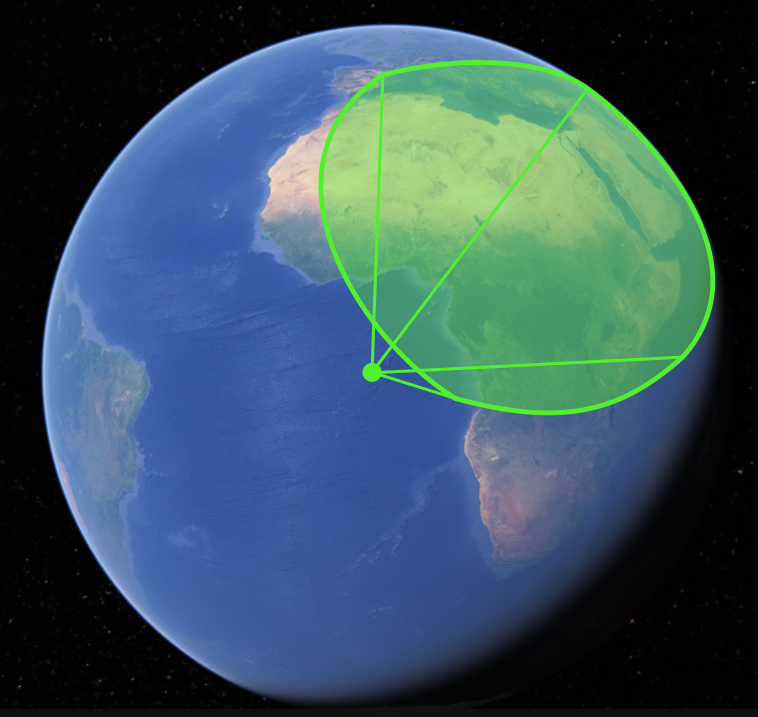
In order to convert the generated vector into latitude and longitude values (Φ,λ), we take the (x, y, z) components of the intersection vector I into our equations for transferring to spherical coordinates.

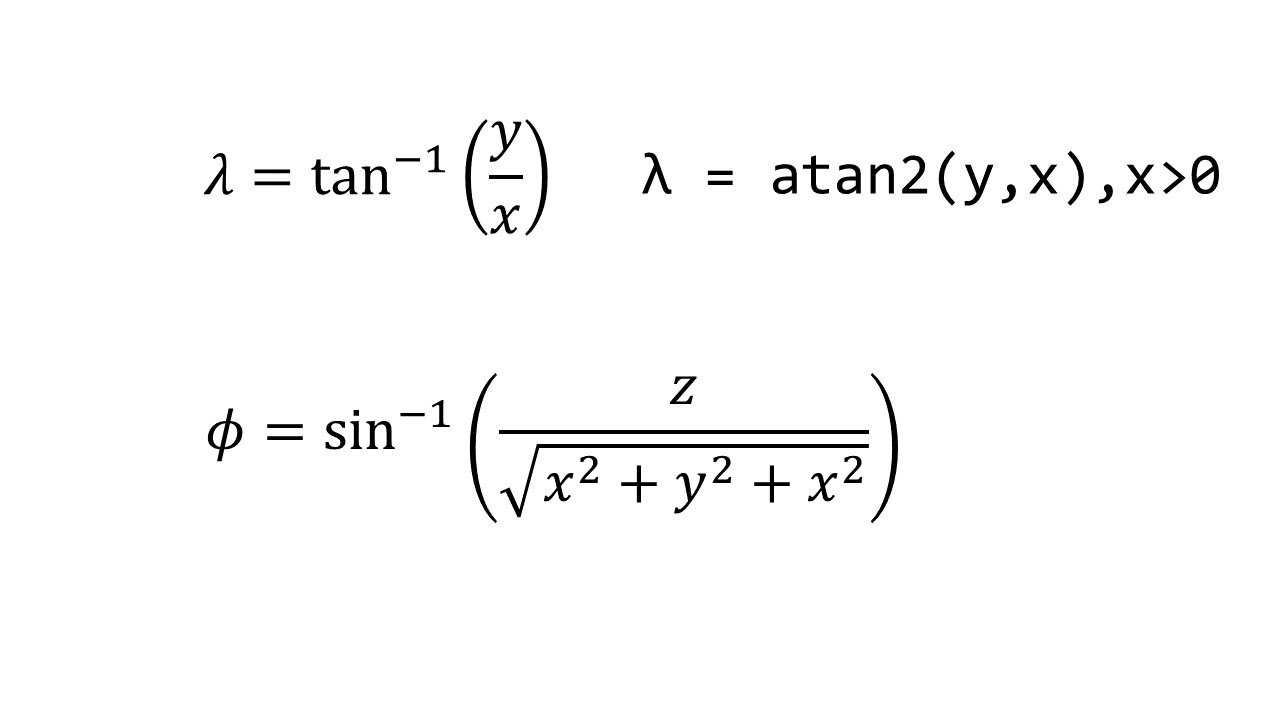
Let's Get Coding!

Copy and paste your own code into your IDLE and follow the instructions. You can also copy the coordinates of any mosque in your own knowledge. You can also confirm the latitude and longitude of the points by using Google Maps (since we don't have access to Gibson's expensive database from the ATLAS system). You can also confirm the bearing of the mosque's Qibla direction using an online map bearing tool (or using linear equations). I recommend acquiring the bearings and positions from Nabatean.net. Make sure to install the correct libraries: numpy, matplotlib and math.

import numpy as np
import matplotlib as plt
import math
#Petra----------------------------------------------------------------------------
#Xian Mosque, China
#23°8′53.74″N,113°15′19.61″E
#Bearing = 295°

#Sahi Ramdah Mosque, Oman
#23°32′35.66″N,58°23′54.11″E
#Bearing = 292.79°

#Kilwa, Tanzania
#8°57′32.93″S,39°29′53.86″E
#Bearing = 356°

#Al-Sawaf Mosque, Iraq
#36°11′0.70″N,44°0′11.50″E
#Bearing = 234.35°

#Siraf Early Mosque, Iran
#27°40′5.62″N,52°19′53.08″E
#Bearing = 282.1°

#Odigram Mosque, Pakistan
#34°44′35.31″N,72°18′51.17″E
#Bearing = 273°

#Mecca----------------------------------------------------------------------------
#Tiberias Friday Mosque, Israel
#32°46′34.59″N,35°32′38.39″E
#Bearing = 160°

#Qasr Hallabat Mosque, Jordan
#32°5′33.73″N,36°19′42.38″E
#Bearing = 163.55°

#Salalah Al-Balid Mosque, Oman
#17°0′21.55″N,54°7′50.11″E
#Bearing = 285.05°

#Banbhore, Pakistan
#24°45′8.34″N,67°31′19.00″E
#Bearing = 265.78°

#Asnaq Friday Mosque, Iran
#38°3′43.02″N,47°11′21.41″E
#Bearing = 207.11°



def dms_to_dd(dms_str):
    def convert_dms_to_dd(dms):
        # Split the DMS string into components
        dms = dms.strip()
        # Split by degrees
        degrees_split = dms.split('°')
        degrees = degrees_split[0]
        # Split by minutes
        minutes_split = degrees_split[1].split('′')
        minutes = minutes_split[0]
        # Split by seconds and direction
        seconds_split = minutes_split[1].split('″')
        seconds = seconds_split[0]
        direction = seconds_split[1]
        # Convert components to decimal degrees
        dd = float(degrees) + float(minutes) / 60 + float(seconds) / 3600
        # Handle N/S/E/W to determine positive/negative values
        if direction in ['S', 'W']:
            dd *= -1
        return dd

    # Split the latitude and longitude
    lat_str, lon_str = dms_str.split(',')
    lat = convert_dms_to_dd(lat_str.strip())
    lon = convert_dms_to_dd(lon_str.strip())

    return (lat, lon)

def P(lat, lon):
    x = math.cos(math.radians(lat)) * math.cos(math.radians(lon))
    y = math.cos(math.radians(lat)) * math.sin(math.radians(lon))
    z = math.sin(math.radians(lat))
    return np.array([x, y, z])

def D(bearing, lat, lon):
    lat_rad = math.radians(lat)
    lon_rad = math.radians(lon)
    bearing_rad = math.radians(bearing)

    N = np.array([
        -math.sin(lat_rad) * math.cos(lon_rad),
        -math.sin(lat_rad) * math.sin(lon_rad),
        math.cos(lat_rad)
    ])

    E = np.array([
        -math.sin(lon_rad),
        math.cos(lon_rad),
        0
    ])

    D = math.cos(bearing_rad) * N + math.sin(bearing_rad) * E
    return D

def cartesian_to_spherical(x, y, z):
    # Calculate the radius
    R = np.sqrt(x**2 + y**2 + z**2)

    # Calculate the latitude
    lat = math.degrees(math.asin(z / R))

    # Calculate the longitude
    lon = math.degrees(math.atan2(y, x))

    return lat, lon

#Example 1

coord1 = str(input(' Enter the coordinates 1, (ensure it is formatted as OO°OO′OO.OO″N/S,OO°OO′OO.OO″E/W) : '))
#"23°8′53.74″N,113°15′19.61″E"
bearing1 = float(input(' Enter the bearing 1: '))
#295

coord1 = dms_to_dd(coord1)
coord1xyz = P(coord1[0],coord1[1])
direction1 = D(bearing1, coord1[0], coord1[1])
Face1 = np.cross(coord1xyz,direction1)

coord2 = str(input(' Enter the coordinates 2, (ensure it is formatted as OO°OO′OO.OO″N/S,OO°OO′OO.OO″E/W) : '))
#"32°29′22.98″N,35°52′48.01″E"
bearing2 = float(input(' Enter the bearing 2: '))
#190

coord2 = dms_to_dd(coord2)
coord2xyz = P(coord2[0],coord2[1])
direction2 = D(bearing2, coord2[0], coord2[1])
Face2 = np.cross(coord2xyz,direction2)

L = np.cross(Face1,Face2)


#We know that the point of intersection must lie within a lattitude (-60,60) and (-25,130)
def select_valid_vector(I1, I2, lat_range=(-35, 60), lon_range=(-25, 130)):
    #"""Select the vector that meets the latitude and longitude conditions."""
    lat1, lon1 = cartesian_to_spherical(I1[0], I1[1], I1[2])
    lat2, lon2 = cartesian_to_spherical(I2[0], I2[1], I2[2])


    # Check if I1 meets the conditions
    if lat_range[0] <= lat1 <= lat_range[1] and lon_range[0] <= lon1 <= lon_range[1]:
        return I1
    # Check if I2 meets the conditions
    elif lat_range[0] <= lat2 <= lat_range[1] and lon_range[0] <= lon2 <= lon_range[1]:
        return I2
    else:
        print("Neither I1 nor I2 meet the conditions. Intersection out of range")
        return None

I1 = L / np.linalg.norm(L)
I2 = -I1
selected_vector = select_valid_vector(I1, I2)

intersect = cartesian_to_spherical(selected_vector[0],selected_vector[1],selected_vector[2])
print(intersect)



import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap

plt.figure(figsize=(12, 8))
map = Basemap(projection='merc', llcrnrlat=-20, urcrnrlat=50,
              llcrnrlon=-25, urcrnrlon=130, resolution='i')

lat_petra = 30.327947
lon_petra = 35.443665
x_petra, y_petra = map(lon_petra, lat_petra)
map.plot(x_petra, y_petra, 'bo', markersize=5)
plt.text(x_petra, y_petra, 'Petra', fontsize=12, ha='left')


lat_mecca = 21.422300
lon_mecca = 39.826202
x_mecca, y_mecca = map(lon_mecca, lat_mecca)
map.plot(x_mecca, y_mecca, 'bo', markersize=5)
plt.text(x_mecca, y_mecca, 'Mecca Point', fontsize=12, ha='left')

# Define the coordinates of the point you want to plot
lat1 = coord1[0]
lon1 = coord1[1]
x1, y1 = map(lon1, lat1)
map.plot(x1, y1, 'bo', markersize=5)
plt.text(x1, y1, 'Mosque 1', fontsize=12, ha='right')

lat2 = coord2[0]
lon2 = coord2[1]
x2, y2 = map(lon2, lat2)
map.plot(x2, y2, 'bo', markersize=5)
plt.text(x2, y2, 'Mosque 2', fontsize=12, ha='right')

lat_inter = intersect[0]
lon_inter = intersect[1]
x_inter, y_inter = map(lon_inter, lat_inter)
map.plot(x_inter, y_inter, 'bo', markersize=5, color = 'red')

map.drawcoastlines()
map.fillcontinents(color='white', lake_color='lightblue')
map.drawmapboundary(fill_color='lightblue')

map.drawgreatcircle(lon1, lat1, lon_inter, lat_inter, linewidth=2, color='r')
map.drawgreatcircle(lon2, lat2, lon_inter, lat_inter, linewidth=2, color='r')
# Plot the point

plt.title('Where do the Two Qibla lines intersect?')
plt.show()
# Create a Basemap instance

Let the Results Speak

Enter the map coordinates of the first mosque (in the correct format as mentioned in the input).
Enter the bearing of the first mosque (without the degree symbol).
Enter the map coordinates of the second mosque (in the correct format as mentioned in the input).
Enter the bearing of the second mosque (without the degree symbol).

In this example, we will use the Xian Mosque in China and the Sahi Ramdah Mosque in Oman, both built in 629 AD and in the 8th century AD respectively.

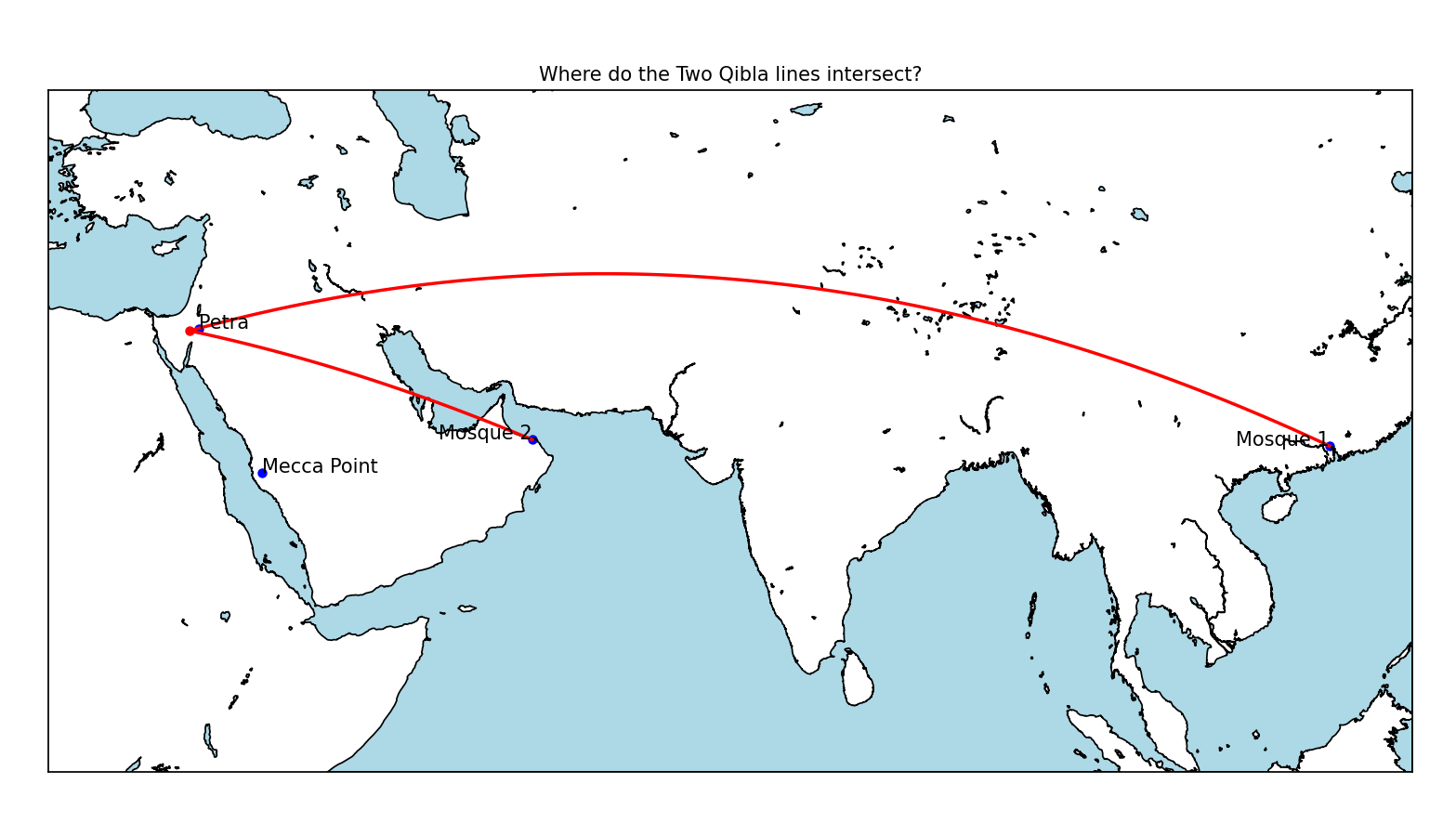
Try this yourself, and you will be surprised. If you do not wish to use the databank from Nabataeans.net, I have also copied the data for your convenience.

Then, as we look at mosques which are built much later, such as the the Banbhore in Pakistan, built in 727 AD, and the Asnaq Friday Mosque in Iran, built in the 9th century, both of them face an inaccurate point around Mecca.

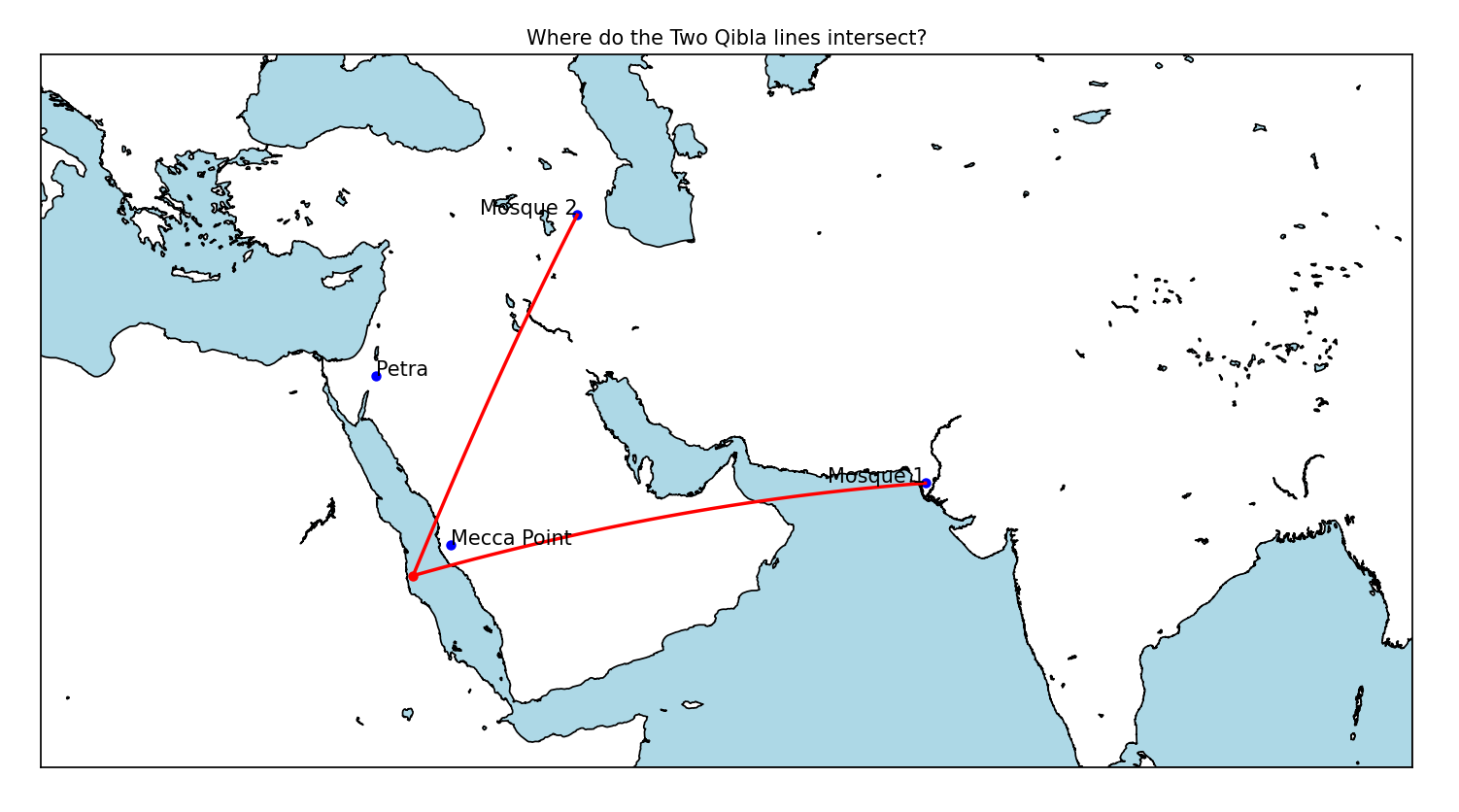
If we categorise the qibla directions according to where they face most closest to, we can see that overtime the direction has shifted:

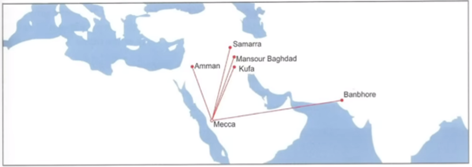
624 AD - 772 AD - Petra

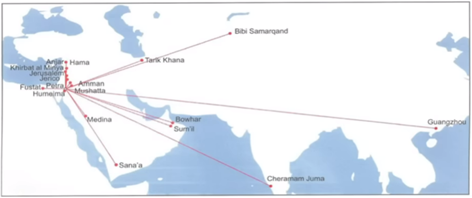
706 AD – 772 AD - In Between

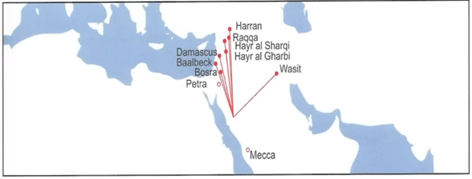
732 AD – 866 AD - Parallel

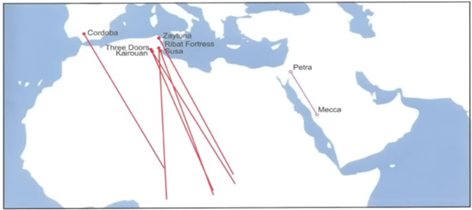
727 AD – 876 AD - Mecca

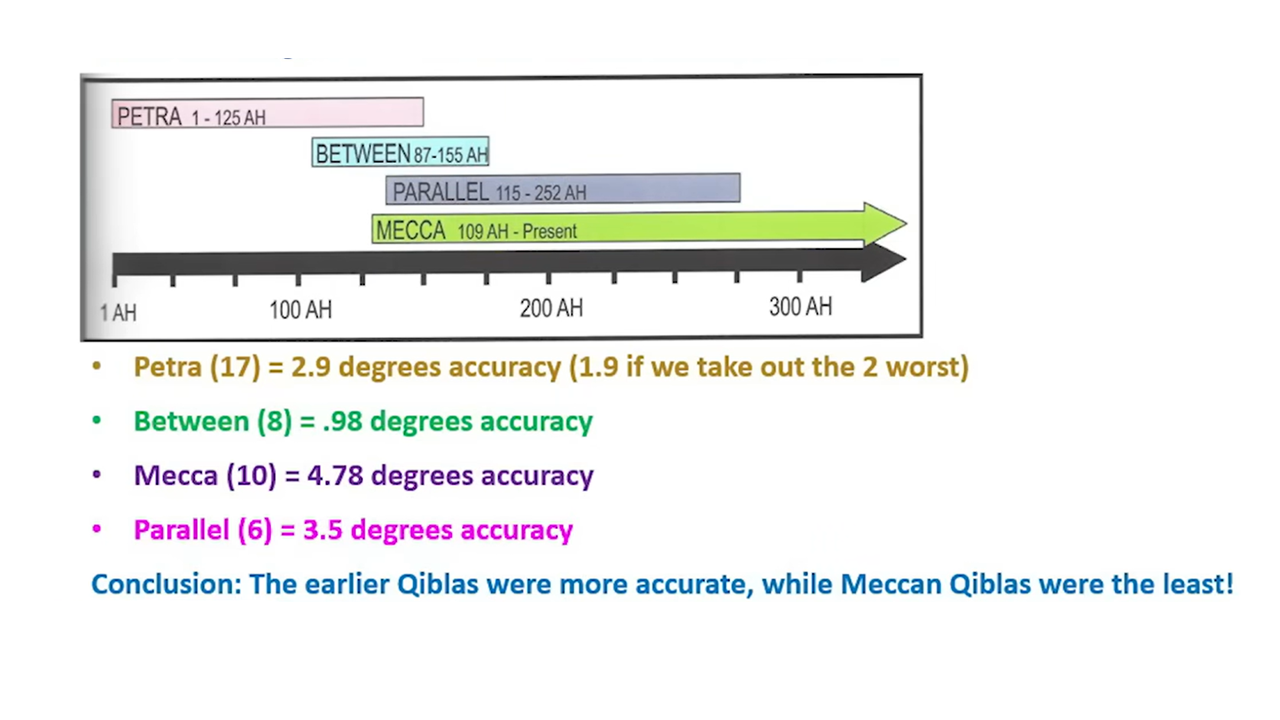
In more detail, we can see that the degree of precision of the Meccan qibla mosques actually becomes worse (not better) than the the Petra qiblas.

Liars, Thieves and False Teachings

How did the Muslim community react to Gibson's theory? Instead of analysing Gibson's data, or even having a meaningful dialogue with him, Islamic mullahs and scholars simply attack his credentials and his degrees. When did we need a degree to show that 2+2 = 4? When did we need a scientist to show that if you point somewhere, then you are pointing at exactly where you are pointing to?

Imagine spending 25 years in the field, analysing the data, being in the Middle East, on the ground, right there with the mosques, learning the language of Arabic, and some old git like David King, claiming to be the leading authority in Islamic history from the safe confines of the UK, calls out your theories as rubbish purely based on the fact that you "don't have a PhD".

Does Dan Gibson have a PhD? No. But do you? Do any of these so-called 'scholars' have any impactful piece of research which would qualify them to discredit someone else's research?

No.

In fact, David King pointed out that the angular error acceptable in Islam is 45° !

What do Muslims further say about Gibson's theory? They say it is a conspiracy from the West to dismantle the Islamic faith, that it is a complete fabrication designed by Governments of the West to control and spread doubt amongst the believers. Furthermore, Muslims are even willing to bash their own ancestral brilliance by saying the ancient Bedouin tribes were not good at precision navigation. In essence, they largely dismiss Gibson's arguments, bash his credentials, and make no effort to make a counter argument. How can you trust the views of someone who simply slanders and dances around the problem with lies, deception and belittlement.

Dan Gibson has done everything necessary to make his theory as clear as possible, with each point having a plethora of evidence to back it up. This is an injustice in academia, research and history the likes we have never seen before. It is utterly appalling that Muslims, Muslim scholars and historians have silenced Gibson's clear and concise proof that the earliest mosques never faced Mecca. The reaction from Muslims clearly demonstrates that there is a clear problem when it comes to freethinking within Islam. Is Islam a religion which upholds the truth, gives freedom of thought or even freedom of speech? If you are strong in your beliefs, then why can't Muslims evaluate the evidence and the arguments made?

Is it not every Muslim's right to know this information? Wouldn't someone from Saudi Arabia be interested in this clear proof of geometry and mathematics? Why are the mullahs, the sheikhs and Islamic scholars stealing the educated Muslim's opportunity to think for himself and become a critical thinker? Does Islam not uphold mathematics, historical facts, and the Truth?

To find more information on Dan Gibson's research, a summary of his findings is laid out in more depth in his documentary The Sacred City (2016) which has been translated into more languages than I can count.

You can also try it out yourself with the interactive Qibla tool, showing clearly the direction of multiple Qiblas of some of the oldest mosques in Islamic history.

Future considerations

The Earth is not entirely a perfect sphere, it slightly bulges by less than 15 miles: The distance from the centre of the Earth to the equator is about 3,963.2 miles. The distance from the centre of the Earth to the poles is about 3,949.9 miles. Does this deviation have any effects on our Great Circle paths.

Using Spherical Geometry to Show that Early Mosques of Islam were NOT facing Mecca.