Signal Processing and Systems in Programming – Guide for Beginners

Signal processing is an important field in engineering and programming.

Basically, it allows engineers and programmers to improve data so that people can use it more effectively.

For example, it is thanks to signal processing that much of the background noise in a phone call is removed. This way, only your voice arrives on the other end of the call.

Other examples are:

• Audio and music software
• Image and video processing software
• Medical imaging software
• Speech and language processing software
• Wireless communication software

Understanding signal processing and systems is key for any programmer who needs to process, manipulate, and analyze these types of data.

This tutorial will explore the field of signal processing and the main characteristics of a system, including some important system characteristics such as:

• Causality
• Memory
• Time-invariance
• Linearity

Here's what we'll cover:

1. What is Signal Processing?
2. Python Code Example – How to Filter a Signal
3. Background on the Fourier Transform
4. What is a System in Signal Processing?
5. Conclusion

What is Signal Processing?

Signal processing, simply explained, is the field where tools are created for engineers and programmers to manipulate certain signals to solve problems.

It involves analyzing sounds or images to extract only the needed data.

For example, the data from biosensors that shows how much oxygen there is in your blood is displayed in a pulse oximeter. This data is filtered with the help of tools from signal processing.

Photo by cottonbro studio

This data processed in a program inside the oximeter with the help of signal processing software tools.

Also, when you're making a phone call to a friend, signal processing algorithms are running so that only your voice gets sent to your friend to reduce as much background noise as possible.

Photo by Karolina Grabowska

Often, signal processing works with the help of tools like the Fast Fourier Transform. And don't worry – I'll explain what this is.

Using the Fast Fourier Transform algorithm, we are able to decompose a signal to find the individual waves that make it up.

This way, we are able to remove the individual waves that we don't want (for example, the background noise of a phone call is a set of waves we can remove to improve quality).

The Fast Fourier Transform is also used as a building block or inspiration for some file compression algorithms.

In the end, this is what signal processing is all about: decomposing a signal to extract what we want from it.

Where is signal processing used in real life?

• Audio processing – like removing the background noise from a movie
• Image processing – like making the image black and white
• Wireless communications systems – like modulating a signal so that it can travel further (frequency modulation)

Python Code Example – How to Filter a Signal

You don't need to understand the full code I am about to show you right now – this is just the code I used to generate the graphs I will show you to help you understand how the Fast Fourier Transform works.

I've shared the full code in the conclusion in a GitHub repository so you can check it out.

Here is the code that filters a signal:

import numpy as np
import matplotlib.pyplot as plt

t = np.linspace(0, 1, 300, endpoint=False)
x = np.sin(2np.pi10t)
y = 0.5np.sin(2np.pi20t)
w = 0.2np.sin(2np.pi50t)
z = x + y + w

zf = np.fft.fft(z)

N = len(z)
freq = np.fft.fftfreq(N, d=t[1]-t[0])
spectrum = 2/N * np.abs(zf[:N//2])

mask = np.ones(len(freq), dtype=bool)
mask[(freq > 15) & (freq < 60)] = False
mask[(freq < -15) & (freq > -60)] = False

zf_filtered = zf.copy()
zf_filtered[~mask] = 0

z_filtered = np.fft.ifft(zf_filtered)

Below i will show visually what each part of the code does with graphs:

Step 1: Creating the signals

t = np.linspace(0, 1, 300, endpoint=False)
x = np.sin(2np.pi10t)
y = 0.5np.sin(2np.pi20t)
w = 0.2np.sin(2np.pi50*t)
z = x + y + w

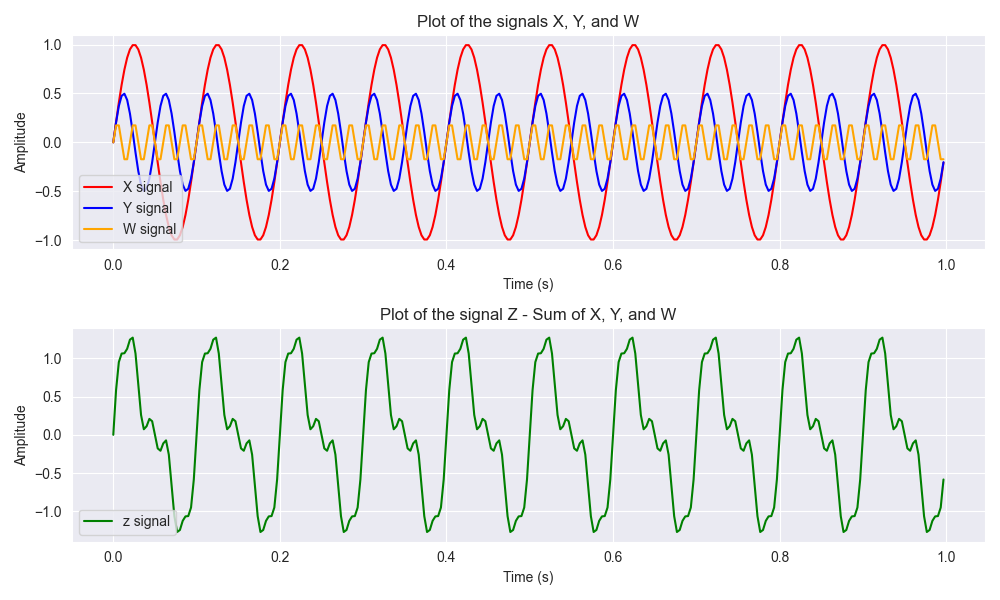Three different signals and a green signal representing their sum

We can see here that the green signal is the sum of:

• Red wave – X signal
• Blue wave – Y signal
• Orange wave – W signal

Note that any signal can be composed of a certain number of simple waves. In mathematics, these waves are the sine and cosine functions.

This incredibly important idea is called a Fourier series.

Below is a video I recommend that explains simply what a Fourier series is:

Step 2: Creating a Fast Fourier Transform on the signal Z

We can apply the Fast Fourier Transform like this:

zf = np.fft.fft(z)

To make a graph out of it, we still need to do the following:

N = len(z)
freq = np.fft.fftfreq(N, d=t[1]-t[0])
spectrum = 2/N * np.abs(zf[:N//2])

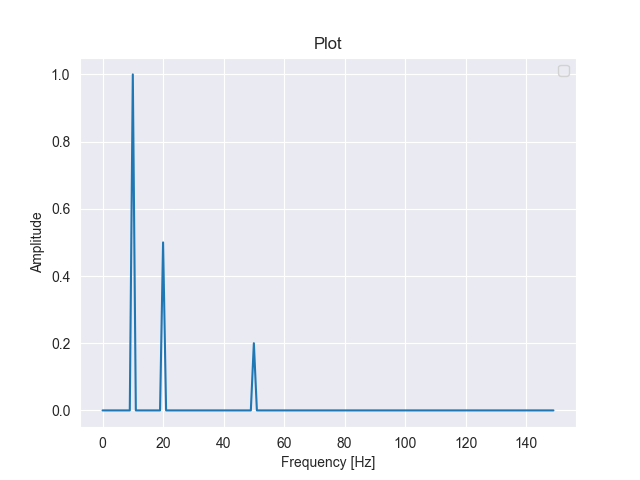Seeing the green signal in terms of frequency instead of time - We are "seeing" the green signal from another point of view

Thanks to the Fast Fourier Transform, we are able to see the composition of the green signal.

As we can see, the green signal is composed of 3 waves with 3 different frequencies:

• 10 hertz – Red wave – X signal
• 20 hertz – Blue wave – Y signal
• 50 hertz – Orange wave – W signal

Step 3: Creating and applying the filter

mask = np.ones(len(freq), dtype=bool)
mask[(freq > 15) & (freq < 60)] = False
mask[(freq < -15) & (freq > -60)] = False

zf_filtered = zf.copy()
zf_filtered[~mask] = 0

z_filtered = np.fft.ifft(zf_filtered)

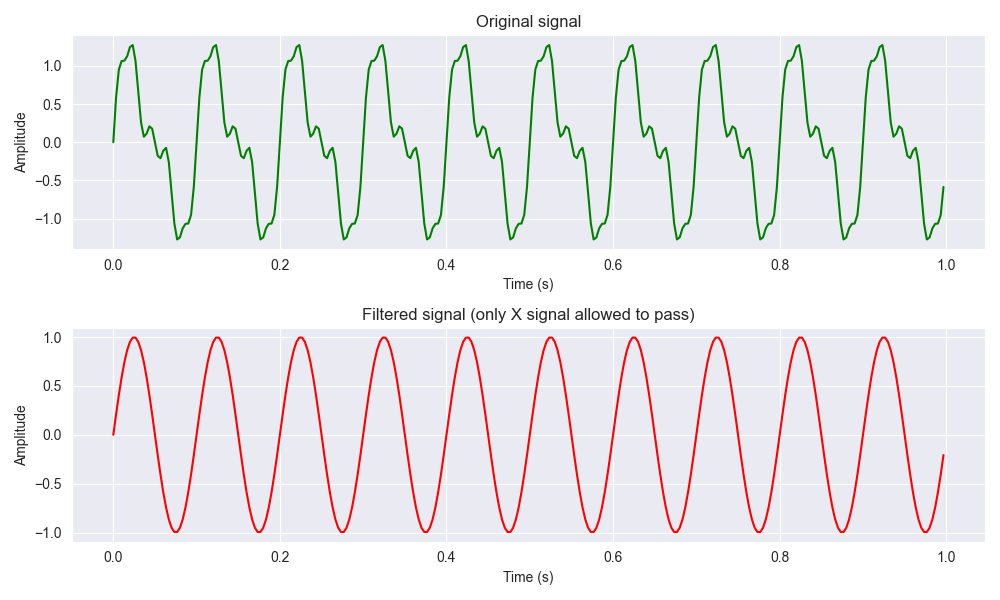Filtered X signal from the green signal - Only the 10 hertz signal passes

This filter is called a pass-band filter, because it filters all the frequencies between 30 hertz and 60 hertz.

So, this filtered red signal is essentially the original red signal.

Background on the Fourier Transform

The idea that any signal can be represented by the sum of simple waves was created by the mathematician Joseph Fourier.

These waves are called sine and cosine.

Note: you don't need to understand these equations completely – I'm just showing them so you can understand the history of the Fourier Transform.

This is what is called a Fourier series:

Equation for Fourier series

Here is a better image of the equation

The coefficients are given by the following:

Coefficients of the Fourier series

From the Fourier series the Fourier transform can be deduced:

Fourier transform equation

Here is a better image of the formula

However, the Fourier transform was developed by various mathematicians and physicists over the years.

So, it was based on the work of many scholars over time that we were able to redefine the Fourier transform.

But this is not the pure mathematical complicated expression that is running in a computer.

In a computer, it is an algorithm that approximates very well the Fourier transform called the Fast Fourier Transform.

That is where in the code the FFT comes from:

zf = np.fft.fft(z)

fft stands for Fast Fourier Transform.

Here are the docs with the function:

But you might be asking...

Why use the Fast Fourier Transform?

Because the Fast Fourier Transform runs much faster than the pure mathematical equation.

There is even a whole field of mathematics dedicated to finding algorithms that approximate pure math so that computers can run it really fast.

This field is called Numerical Analysis.

It is also used to find approximate solutions for problems that are impossible to find by hand.

For example, in the field of partial differential equations, many solutions to partial differential equations are only solved with numerical analysis methods running on computers.

This way, thanks to this field of mathematics, companies are able to save millions in energy costs

If you are interested in learning more about numerical analysis, I've included some more resources in the conclusion.

Changing the topic slightly, now we will talk about systems

What is a System in Signal Processing?

A system is a combination of many “things” that work together as if they were a whole.

An example of a system could be a computer or a car.

In signal processing, a system is often a combination of software and hardware in a technology that takes an input signal and produces an output signal.

For example, when pressing the acceleration pedal in a car (input), the car goes faster (output).

Knowing the characteristics of a system is important for understanding how it will process the signal.

Four important characteristics of a system are:

• Causality
• Memory
• Time-invariance
• Linearity

But, why is it important to understand the main characteristics of a system in programming?

By understanding these characteristics, you will understand better how to design software (in this case, the system can be seen as software) as well as how to optimize and integrate it.

Knowing these characteristics is very important in systems engineering where they are applied to software development. They help you manage the complexity of programs, define their requirements, and ensure quality, adaptability and scalability.

If you want to learn more about systems engineering, you can read my article on it.

So, let's learn more about what each of these characteristics are.

Causality

Causality is the property of a system where the output depends on past and present input only.

For example, when predicting the weather, it is only possible to use past weather data to make a forecast.

It is not possible to use future weather data to predict the weather.

Memory

Memory is the property of a system where the output depends on past inputs.

Recommendation systems used by websites like Netflix and Amazon suggest movies or products based on a user's previous interactions.

The algorithms take into account products viewed or purchased, and use this information to recommend similar items.

With more data gathered over time, recommendations become more accurate and personalized.

Memory is important in programming because it allows us to create systems that can learn and adapt over time – for example, machine learning systems.

Time-invariance

Time-invariance is the property of a system when the output does not depend on when the input was applied.

Real-time control systems used in robotics, manufacturing, and aerospace applications rely on time-invariant systems.

For instance, a flight control system must respond quickly and accurately to changes in an aircraft's position, irrespective of when they occur.

Linearity

Linearity in programming is like a recipe where doubling the ingredients results in a proportionally doubled output, allowing for predictable and accurate results.

Linearity refers to the property of a system where the output is directly proportional to the input.

This means that if the input is doubled, the output will also be doubled.

For example, in digital image processing, linearity is used in techniques such as contrast adjustment and color correction to ensure that the output is proportional to the input.

This results in predictable and accurate image processing.

Conclusion

Signal processing and systems are essential for programming because they allow us to process, manipulate, and analyze data in a reliable and predictable way.

Whether you are working on audio processing, image processing, or any other application that involves signal processing, understanding the fundamentals of signal processing and systems is crucial for success.

Systems are closely related to signal processing, because they allow the transformation of signal for programmers and engineers to reach their desired goal.

If you are interested in learning more about Fourier Transform, here is a YouTube video explaining it in more depth:

Here is a YouTube video explaining the algorithm that actually runs on your computer:

And here is also a video detailing the history of the development of the Fast Fourier Transform:

Final Note

There are more transforms used for signal processing and other purposes, such as the Laplace transform (used in continuous signals) and the Z transform (used in discreet signals).

But, since there are so many mathematical transforms formulas, what really is a transform?

A transform is simply a mathematical tool that helps us see something from a different point of view.

By seeing things a different way, we can learn about details we did not see originally.

For example, with the Fourier Transform, we can see the signal from the point of view of a frequency instead of the point of view of time.

This lets us see the same thing in a different way.

Mathematically, we can say we are changing the domain of the function. In other words, we are changing the x axis.

And I will leave this with you: the Laplace transform is a generalized Fourier transform.

Full code: